單層體外預應力鋼筋混凝土框架抗倒塌試驗研究

范云蕾，王杰，王皓磊

?

單層體外預應力鋼筋混凝土框架抗倒塌試驗研究

范云蕾，王杰，王皓磊

(中南林業科技大學 土木工程與力學學院，湖南 長沙，410018)

通過兩榀單層雙跨體外預應力鋼筋混凝土框架結構試驗研究，分析中柱失效后結構體系的抗倒塌性能。對試驗模型框架受力過程進行分析，建立基于結構變形的體外預應力筋應力變化分析方法，推導出體外預應力鋼筋混凝土框架倒塌破壞的極限荷載簡化計算公式。研究結果表明：中柱失效后，體外預應力鋼筋混凝土框架的連續倒塌過程分為4個階段即彈性階段、彈塑性階段、受壓混凝土破壞階段和懸鏈線作用階段，結構主要通過壓拱機制和懸鏈線機制進行內力重分配；懸鏈線機制提供的抗力由側向約束的剛度和強度決定，當柱對梁提供的水平約束不足時，框架的倒塌抗力隨豎向位移的增大而不斷下降；體外預應力筋可提高框架的開裂荷載、壓拱作用階段的峰值荷載以及懸鏈線作用階段的極限荷載；采用所提出的公式所得計算結果與試驗結果較吻合，可用來預估體外預應力鋼筋混凝土框架考慮懸鏈線作用的極限承載力。

體外預應力鋼筋混凝土框架；連續倒塌；靜力試驗；懸鏈線作用；預應力

結構抗連續倒塌性能不足是造成建筑結構倒塌的重要原因之一。結構連續性倒塌是由于偶然荷載造成結構局部破壞，并引發連鎖反應導致破壞向結構的其他部分擴散，最終使結構主體喪失承載力，整個結構大范圍倒塌。最早的建筑結構抗連續倒塌規定中要求建筑結構在意外荷載作用下不應發生與初始破壞不相稱的大范圍倒塌[1]。一些發達國家和地區也先后在其設計規范和設計指南中增加或完善了結構抗連續倒塌的設計條文[2?7]。美國還制定了專門的抗連續倒塌設計規范[8?9]，對抗連續倒塌設計目標、計算分析方法和結構構造要求等進行了詳細規定。框架結構在倒塌過程中，懸索作用對結構的連續倒塌起著重要的減緩與抑制作用，且該懸索作用使得框架梁在倒塌極限狀態時的承載力比基于小擾度破壞準則時的承載力高出許多，也是偶然荷載導致主要支撐構件失效后可能觸發連續倒塌的原因[10]。因此，研究懸索作用機理與破壞形態具有重要意義。KHANDELWAL 等[11]采用數值模擬方法分析了鋼梁柱組合結構倒塌過程中的懸索作用效應。ASTANEH等[12]進行了4組單層鋼框架結構的抗倒塌試驗，其研究結果表明在鋼?混凝土組合樓板下安裝錨固可靠的拉索，可提高結構的抗倒塌性能。YI等[13]進行了一榀三層四跨框架平面擬靜力抗倒塌試驗，并對框架懸索作用進行了研究與分析，提出預估倒塌極限承載能力的方法。何慶峰等[10]通過變化配筋率、鋼筋等級、加載速度等方式完成了5個約束梁試驗，研究了鋼筋混凝土柱失效情況下，梁柱子結構在考慮懸索作用效應時的抗倒塌性能。STINGER等[14]按1/4縮尺比例進行了3組二層二跨鋼筋混凝土平面框架的倒塌試驗，其研究結果表明部分填充墻對框架在壓拱作用階段的承載能力并沒有很大提高，倒塌過程中結構主要通過壓拱機制和懸鏈線機制進行內力重分配。李鳳武等[15?16]按1/2縮尺比例進行了三層三跨鋼筋混凝土空間框架的動力倒塌試驗，通過研究破壞瞬間結構的位移反應、加速度反應、鋼筋應變和裂縫分布情況，揭示了結構在豎向構件失效時的抗倒塌性能。王浩等[17]進行了一榀非對稱的單層RC平面框架靜力倒塌試驗，分析了該框架在局部豎向構件失效后的水平向連續倒塌的受力機理和倒塌抗力。初進明 等[18]設計制作了8個1/3比例的鋼筋混凝土單向梁板子結構試件，分析了截面尺寸、配筋率等參數對鋼筋混凝土樓蓋系統抗連續倒塌性能的影響。周育瀧等[19]研究了鋼筋混凝土框架抗連續倒塌的壓拱機制分析模型。HOU等[20?21]進行了1/3比例的單層雙跨雙開間鋼筋混凝土空間框架分別在邊柱、中柱失效情況下的靜力倒塌試驗，并分別探討了梁、板在大變形下的懸鏈線機制和張力膜機制。目前人們主要針對鋼筋混凝土結構進行研究，對于體外預應力結構在極端災害下的抗連續倒塌性能研究較少。為此，本文作者設計了一榀單層體外預應力鋼筋混凝土框架，并與普通鋼筋混凝土框架進行對比，以研究體外預應力鋼筋混凝土框架連續倒塌的受力機理與破壞形態。

1 試驗概況

根據某多層鋼筋混凝土結構民用建筑，按1/2.5的縮尺比例設計制作了2個截面尺寸與配筋均相同的兩跨單層鋼筋混凝土框架試件：K0框架為對比框架，未設計體外預應力筋；K1框架為試驗框架，在距離梁底30 mm處平行梁布置1根直徑為15.2 mm的體外預應力筋，有效張拉預應力為744 MPa，采用夾片式錨具錨固。K1框架如圖1所示。框架層高為1.44 m，單跨跨度為2.4 m，B柱設計為失效柱。2個框架均以直徑為12 mm的HRB400級鋼筋作為非預應力縱向受拉鋼筋，實測鋼筋極限抗拉強度和屈服強度平均值分別為610.96 MPa和492.93 MPa；箍筋采用直徑為6 mm的HRB400級鋼筋，實測鋼筋屈服強度平均值為423.39 MPa。混凝土梁、柱采用等級強度為C40的混凝土，在澆筑混凝土時制作了邊長為150 mm的混凝土立方體試塊，測得混凝土立方體抗壓強度平均值為50.7 MPa。

K0框架為對比框架，未設計體外預應力鋼筋。K1框架采用直徑為15.2 mm的鋼絞線為體外預應力筋，有效張拉預應力為744 MPa；鋼絞線平行梁布置，距離梁底30 mm，采用夾片式錨具錨固。

模型框架與反力架分別通過地腳螺栓固定在實驗室地基梁上，機械千斤頂垂直放置于中柱柱頂與反力架之間。在試驗過程中，通過機械千斤頂由上往下進行正向人工分級加載，用靜力方式模擬中柱失效。加載過程采用荷載-?位移雙控制，即在試件屈服之前采用力加載控制，每級5 kN；試件屈服后，采用位移加載控制，每級2~5 mm。在每級加載后，等待5 min，再讀取框架各測點的位移、混凝土以及鋼筋應變。

框架試驗的觀測內容包括中柱下端的軸向力、中柱豎向位移和各柱水平位移。鋼筋表面和柱混凝土表面的應變片測點布置如圖2所示。試驗中，在框架梁的張拉端增加了力傳感器來測量張拉端預應力筋的應力變化情況。

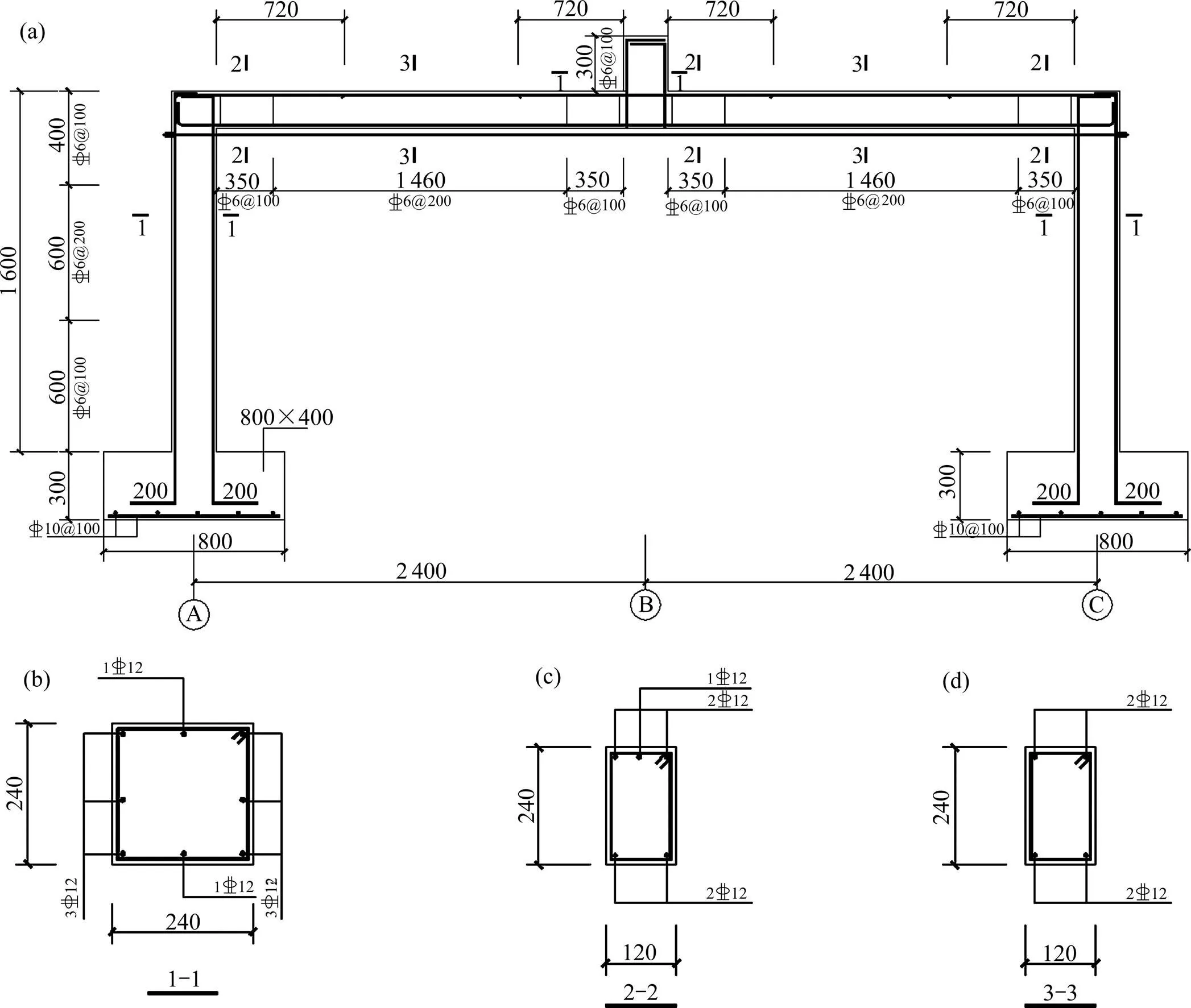
(a) 試件立面圖；(b) 柱截面配筋；(c) 梁端截面配筋；(d) 梁跨中截面配筋數據單位：mm

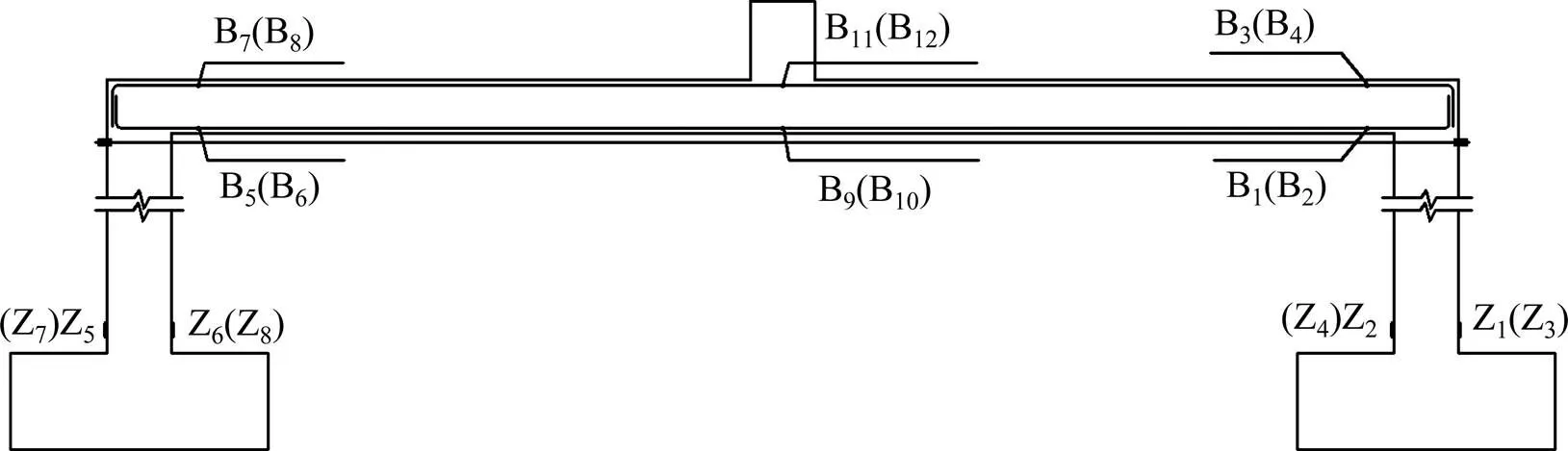
圖2 梁柱鋼筋應變片測點布置

2 試驗結果及其分析

2.1 試件破壞過程

在加載初期，各框架處于彈性工作階段，無明顯破壞現象；當加載到25 mm時，框架梁開始出現斜裂縫，彎曲裂縫也開始傾斜發展；當加載到45 mm時，K0框架柱上端開始出現水平裂縫，框架梁端截面受拉鋼筋發生屈服，受壓區混凝土開始被壓碎；K1框架柱上端出現混凝土剝落，梁端鋼絞線錨固端出現橫裂縫；當加載到145 mm時，K0框架梁端出現明顯貫通裂縫，并且出現很大傾角；K1框架梁端出現明顯貫通裂縫。當加載到254 mm時，K0框架梁跨中截面受壓區混凝土出現大塊剝落，中柱西側10 cm處梁底部鋼筋被拉斷，試件破壞模式如圖3(a)所示。當加載到287 mm時，K1框架梁中柱西側5 cm處梁底部和頂部鋼筋受壓屈曲破壞，試件破壞模式如圖3(b)所示。

2.2 荷載?位移曲線

圖4所示為K0和K1框架中柱豎向荷載?位移關系曲線。從圖4可以看出：曲線可以分為4個工作階段，即彈性階段、彈塑性階段、受壓混凝土破壞階段和懸鏈線作用階段。

在彈性階段，荷載和位移基本呈線性關系，此時構件無明顯破壞現象。當跨中豎向位移分別小于1.8和5.0 mm時，K0和K1框架梁上的裂縫在點以后才發現，此時開裂荷載分別為12.5和29.2 kN。段為彈塑性階段，此時荷載和位移的增加呈非線性關系，框架梁滿布裂縫，框架柱頂部出現橫向裂縫。段為受壓混凝土的破壞階段，從點開始，受壓混凝土局部壓碎，在點(對應中柱豎向位移約145 mm)附近，塑性鉸區域受壓混凝土嚴重剝落。點以后，梁端受彎承載能力基本喪失，結構受力機制轉化為懸鏈線受力機制，主要由鋼筋來直接傳遞荷載。對所測的鋼筋應變進行分析可知：達到極限倒塌狀態時，原來受壓的鋼筋已轉變為受拉，并且部分鋼筋已達到受拉屈服，說明此時構件已經進入懸鏈線作用階段。

(a) K0框架；(b) K1框架

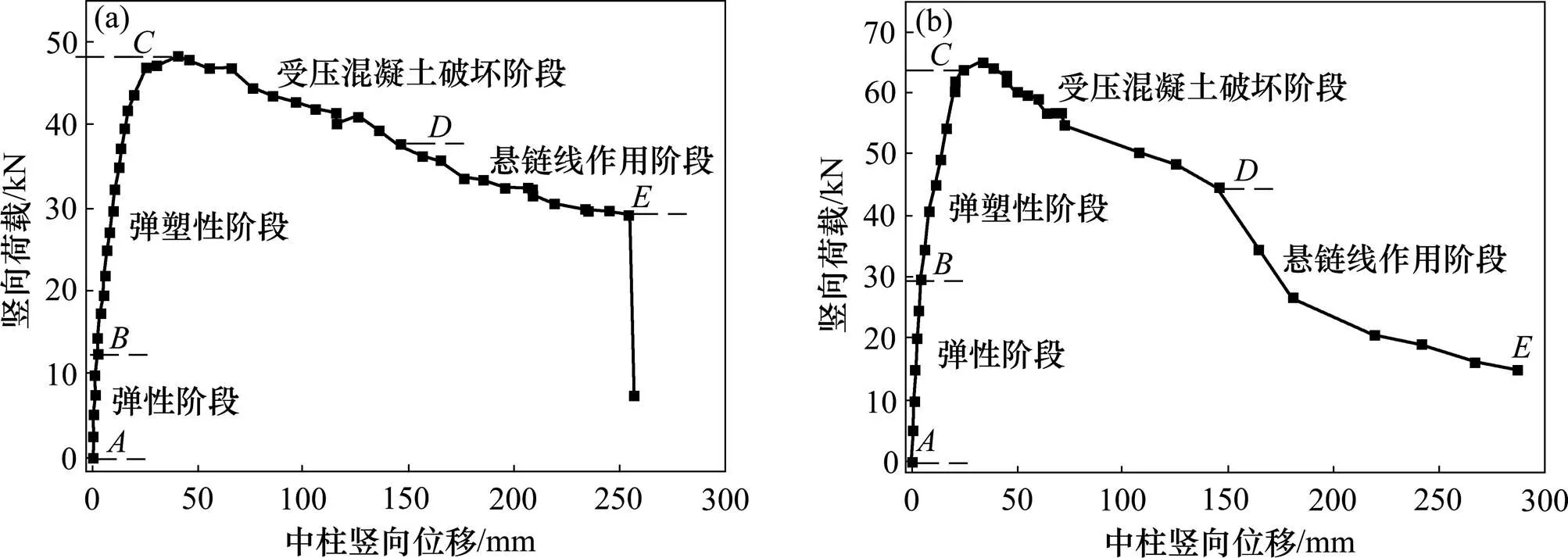
(a) K0框架；(b) K1框架

進入懸鏈線機制后，框架的倒塌抗力并沒有隨著位移增大而迅速提高，而是繼續下降，這與文獻[10]和[13]中的試驗研究結果有顯著區別。這是由于柱對框架梁提供的水平約束能力有限，柱端發生較大的水平位移，這一方面釋放了部分梁端的轉動，使得鋼筋應變增長減緩；另一方面減弱了提供給框架梁的水平約束力。該現象的發生使得框架梁的軸向拉力發展變慢，導致框架的抗倒塌能力并沒有提高，而是繼續下降。當K0框架的中柱豎向位移達到約254.4 mm時，框架梁中柱西側的底部鋼筋被拉斷(見圖3(a))，荷載傳感器的力直接從29.3 kN下降到7.6 kN。為了防止試驗設備破壞，停止試驗。當K1框架的中柱豎向位移達到287 mm時，框架梁跨中偏右側底部和頂部鋼筋受壓屈曲(見圖3(b))，鋼絞線抵到梁底部，提前結束試驗。

表1所示為兩框架臨界點的豎向荷載與中柱豎向位移對比。從表1可以看出：K1框架的開裂荷載是K0框架的2.3倍，對應的豎向位移是K0框架的2.8倍，說明體外預應力鋼筋可以提高框架的開裂荷載。兩框架梁達到最大受彎承載力時的豎向位移大致相等，K1框架對應的豎向荷載是K0的1.35倍。當進入懸鏈線作用階段時，K1框架對應的豎向荷載是K0的1.18倍，說明體外預應力鋼筋可以增大框架梁的最大受彎承載力以及懸鏈線作用階段的承載能力。

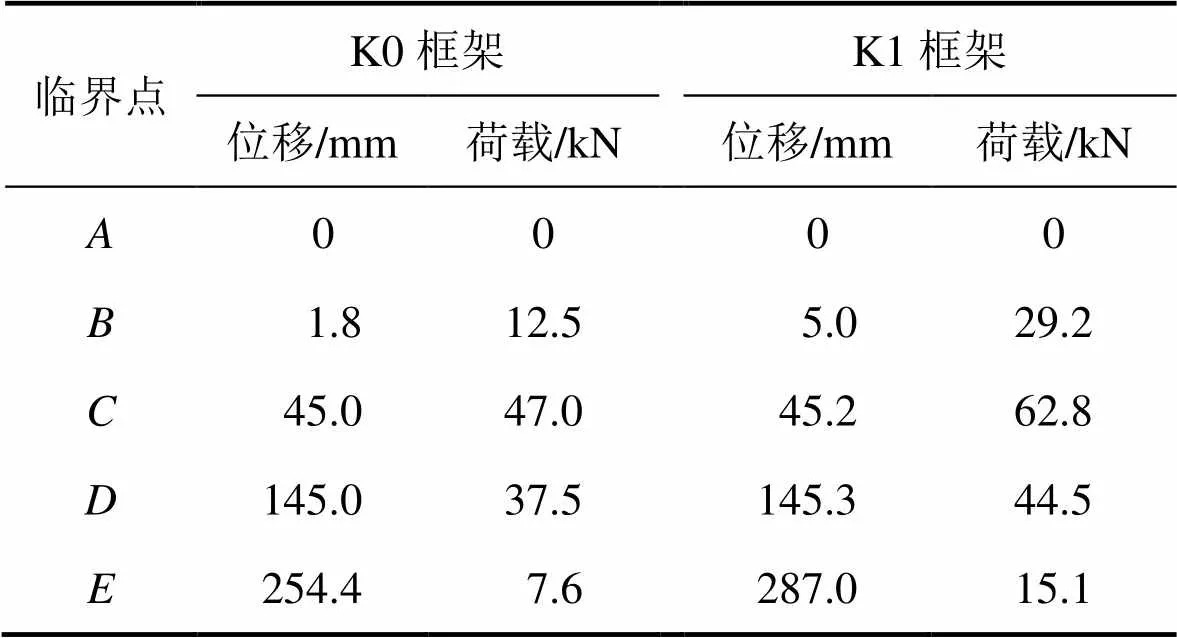
表1 K0和K1框架臨界點的中柱豎向位移與荷載對比

2.3 框架柱水平位移

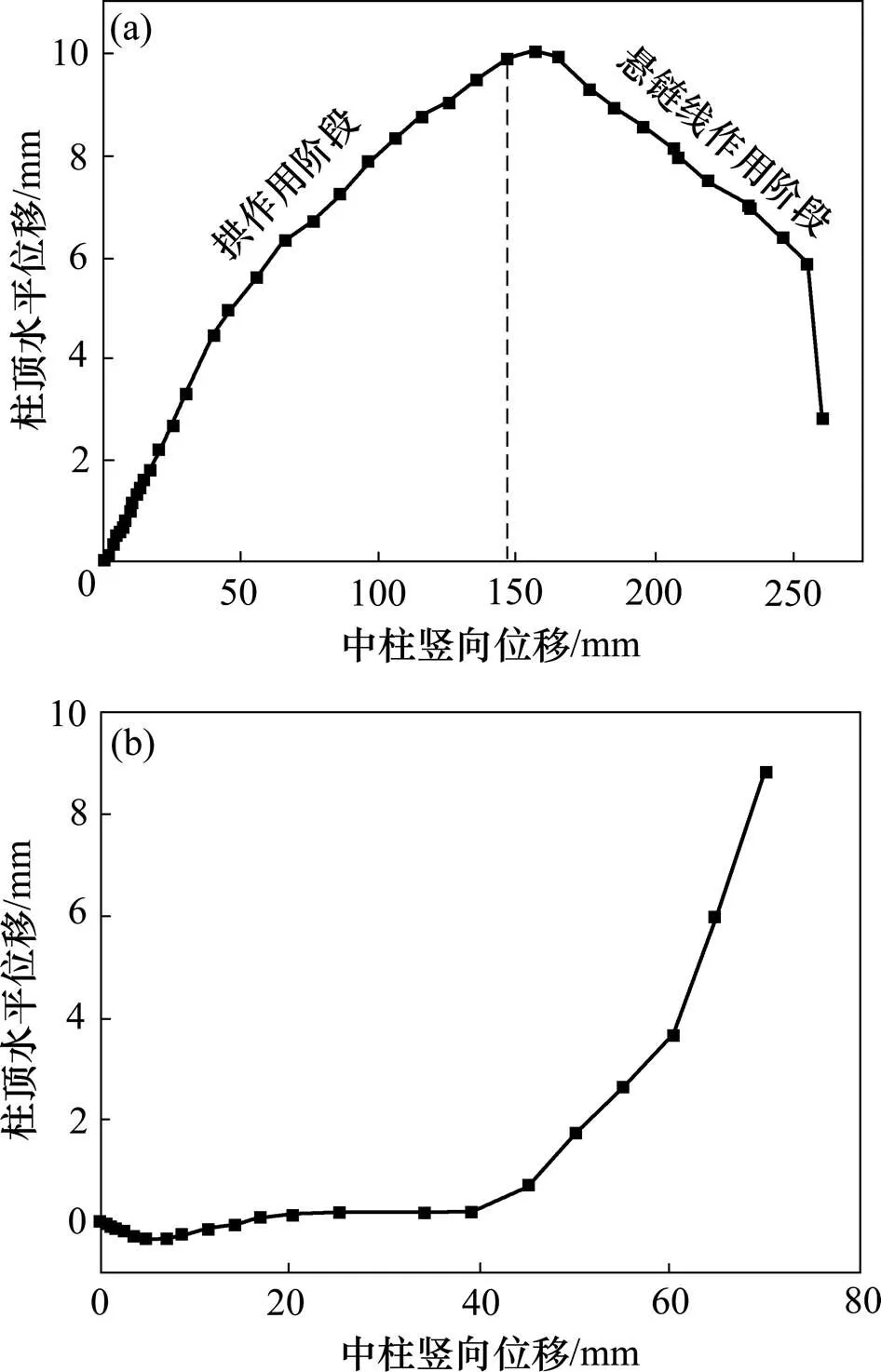
框架柱頂水平位移與中柱豎向位移關系如圖5所示，其中水平位移為正值表示向框架外側移，負值表示向框架內側移。從圖5(a)可以看出：隨著中柱豎向位移增加，K0框架柱頂向外側移，最大位移約為 9.5 mm。在這一階段，梁在中柱近端承受正彎矩，截面開裂后中性軸上移，而在中柱遠端承受負彎矩，中性軸向下移動。

在中柱兩側的框架梁兩端，截面轉動中心不在同一水平面上，框架梁內產生軸向壓力，這就是所謂的“推力作用”或“拱作用”。當中柱豎向位移達到 140 mm左右時，框架柱開始向內運動。這是由于框架梁跨中塑性鉸轉動中心位于其支座塑性鉸轉動中心以下，框架梁內軸向壓力逐漸減小，框架進入“懸鏈線作用階段”。對于K1框架(見圖5(b))，隨著中柱豎向位移增加，框架柱頂向內側移，最大位移量約為 0.33 mm，框架梁處于彈性工作階段。框架梁進入彈塑性工作階段后，框架柱頂開始向外側移。當框架梁進入受壓混凝土破壞階段(此時中柱豎向位移約 45 mm)后，框架柱頂向外急劇移動。當中柱豎向位移達到72 mm時，由于框架柱頂混凝土剝落，無法再測量框架柱頂水平位移。

2.4 鋼絞線內力?位移關系

圖6所示為K1框架鋼絞線內力?跨中豎向位移關系。從圖6可以看出：隨著中柱豎向位移增加，鋼絞線內力增大，最大鋼絞線內力約為195 kN。在這一階段，壓拱作用使框架柱向外側移動從而導致這一階段鋼絞線內力持續增大。當中柱豎向位移達到146 mm左右，框架梁跨中塑性鉸轉動中心位于其支座塑性鉸轉動中心以下時，框架柱開始向內運動，鋼絞線兩錨固端間的距離變小，鋼絞線內力減小，由“拱作用階段”轉化為“懸鏈線作用階段”。

(a) K0框架；(b) K1框架

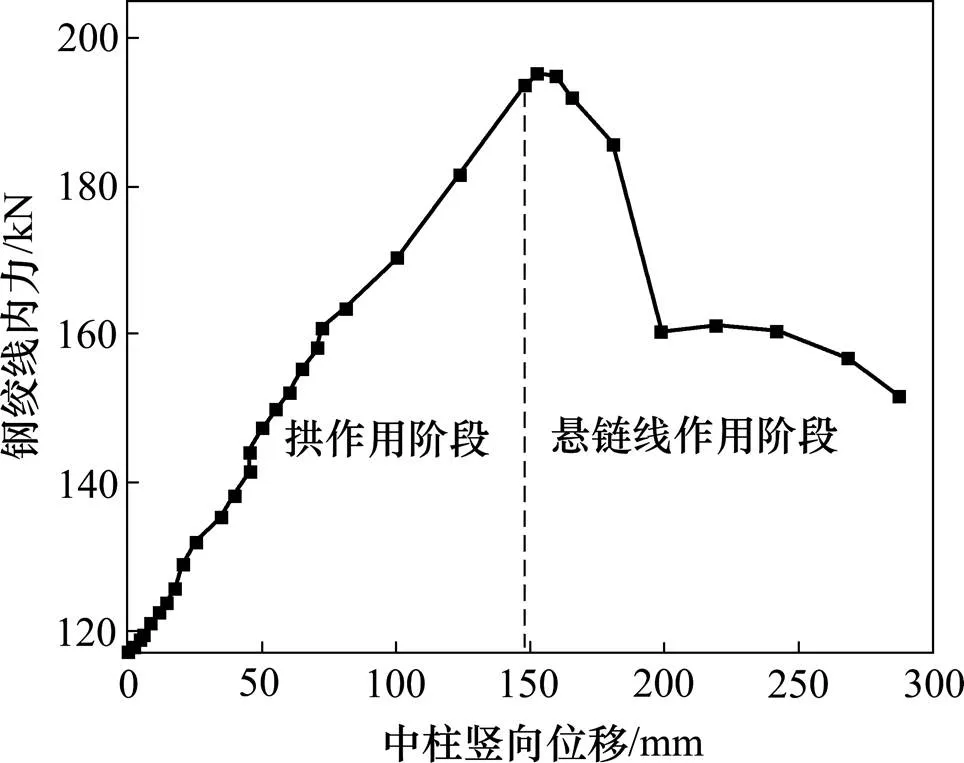
圖6 鋼絞線內力與中柱豎向位移關系

2.5 框架柱底混凝土表面應變

框架柱底混凝土表面應變與中柱豎向位移之間的關系如圖7所示。對于K0框架(見圖7(a))，當中柱豎向位移約145 mm時，框架柱底外側混凝土(Z5下、Z7下，見圖2)達到壓應變峰值，隨后壓應變開始減小；框架柱底內側混凝土(Z6下、Z8下，見圖2)達到拉應變峰值，隨后拉應變開始減小。由此可見，柱下端混凝土表面應變的變化情況與柱頂水平位移變化情況是一致的。當中柱豎向位移達145 mm時，框架水平位移由向外轉為向內。在彎矩和軸力的共同作用下，框架柱底外側受拉而內側受壓，直到柱下端外側出現橫向裂縫后，發生內力重分布。

對于K1框架(見圖7(b))，柱底混凝土應變變化總體趨勢與K0框架的一致。當框架梁的受彎承載能力耗盡，進入受壓混凝土破壞階段時，框架柱頂和柱底外側同時達到峰值應變，隨后開始減小。這表明鋼絞線的存在使得框架的整體性更好。需要說明的是：試驗過程中由于千斤頂行程不夠，進行2次卸載后墊鋼片再加載，導致曲線出現了2個峰值。

2.6 鋼筋應變

圖8~9所示分別為K0和K1框架梁端、跨中截面底部和頂部鋼筋的應變變化情況。

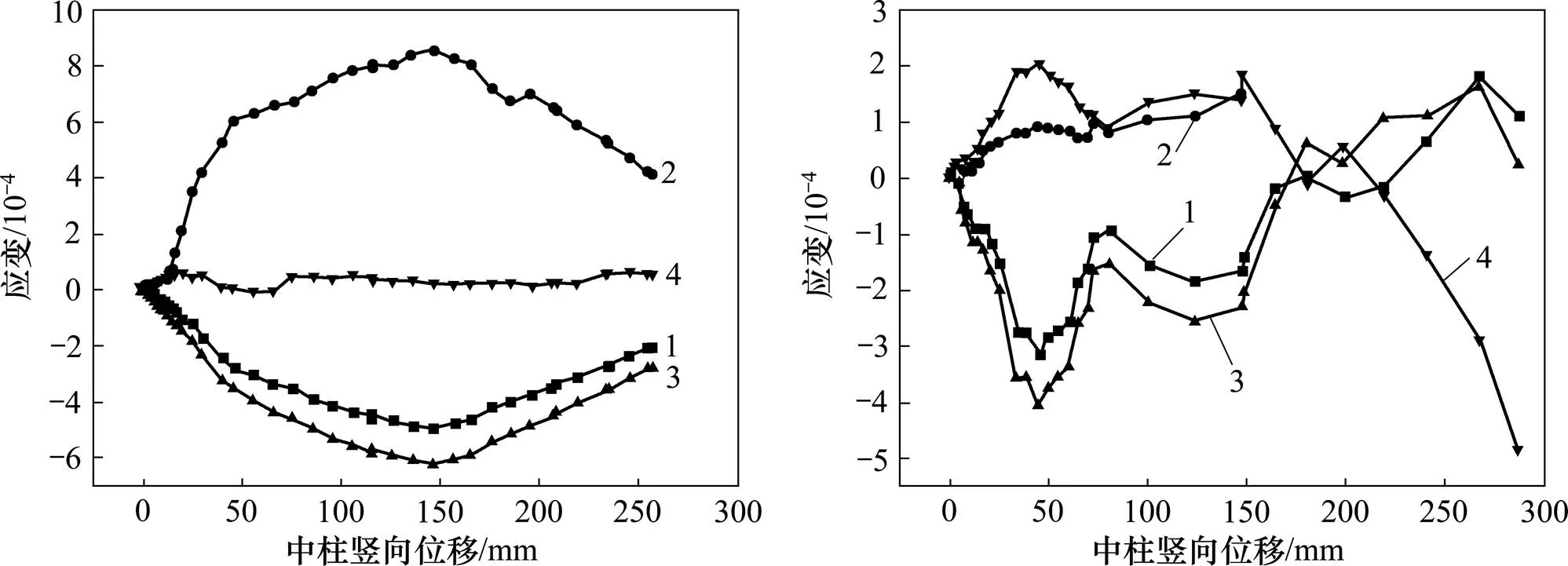
對于K0框架(見圖8)，梁端底部鋼筋(B1和B2)在加載初期承受壓力，但是壓力不大，說明此時大部分壓力由混凝土承擔。鋼筋應變隨著豎向位移增大而緩慢增大，當框架梁的受彎承載能力耗盡時，壓應變達到峰值。隨著框架進入受壓混凝土破壞階段(中柱豎向位移大于50 mm)，鋼筋應變B1和B2所承受的拉應力急劇增加，并且很快達到受拉屈服，這表明懸鏈線作用正在逐漸形成。梁端頂部鋼筋(B3和B4)在加載初期承受拉力，受軸向壓力的影響，頂部鋼筋(B3和B4)的拉應變逐漸減小并變為壓應變，且隨著中柱豎向位移增大，壓應變逐漸增大。框架梁內的軸向力達到峰值后開始減小，受其影響，頂部鋼筋應變也達到壓應變峰值，隨后減小。B4鋼筋應變發生從受壓向受拉轉變，轉變點出現在100~150 mm范圍內，說明此時梁端截面已進入塑性階段。從圖8(a)可知：梁端頂部鋼筋B3和B4均未達屈服。對于跨中截面，底部鋼筋(B9和B10)與頂部鋼筋(B11和B12)在加載初期分別承受拉力與壓力，當中柱豎向位移達到29 mm時，兩者先后達到應變峰值。隨著框架進入受壓混凝土破壞階段(中柱豎向位移大于50 mm)，梁端截面開始塑性轉動，跨中截面底部和頂部鋼筋應變基本保持不變。

(a) K0框架；(b) K1框架

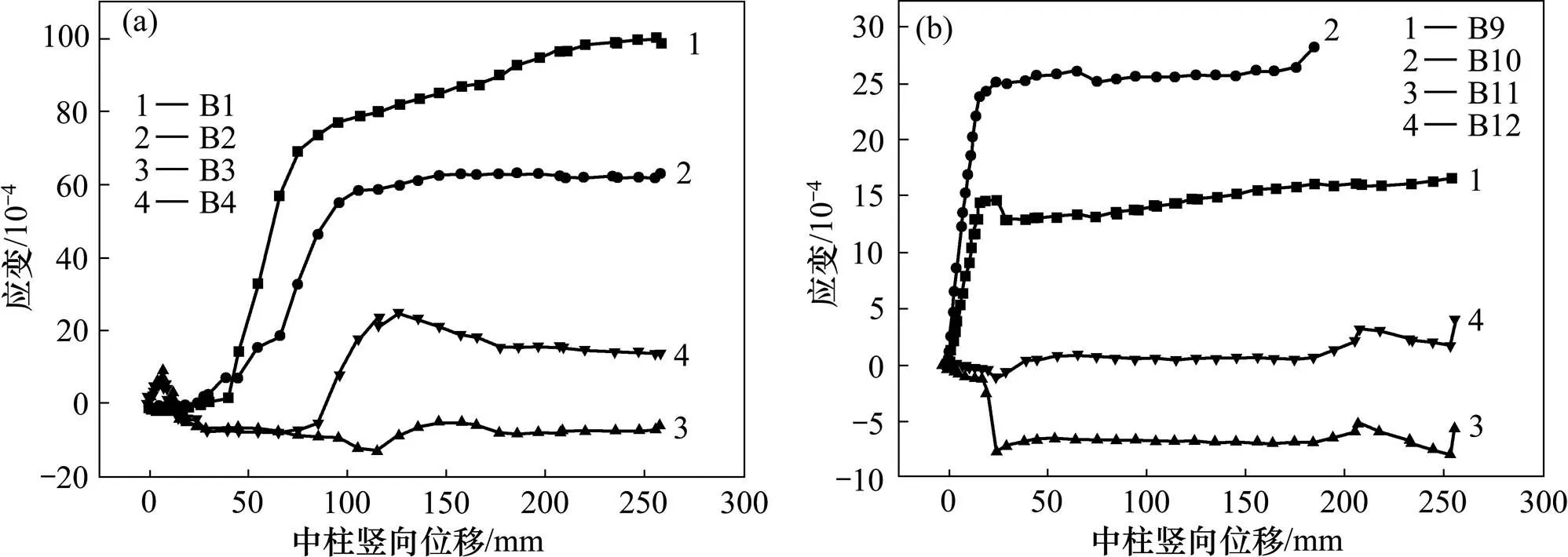
(a) 梁端截面；(b) 跨中截面

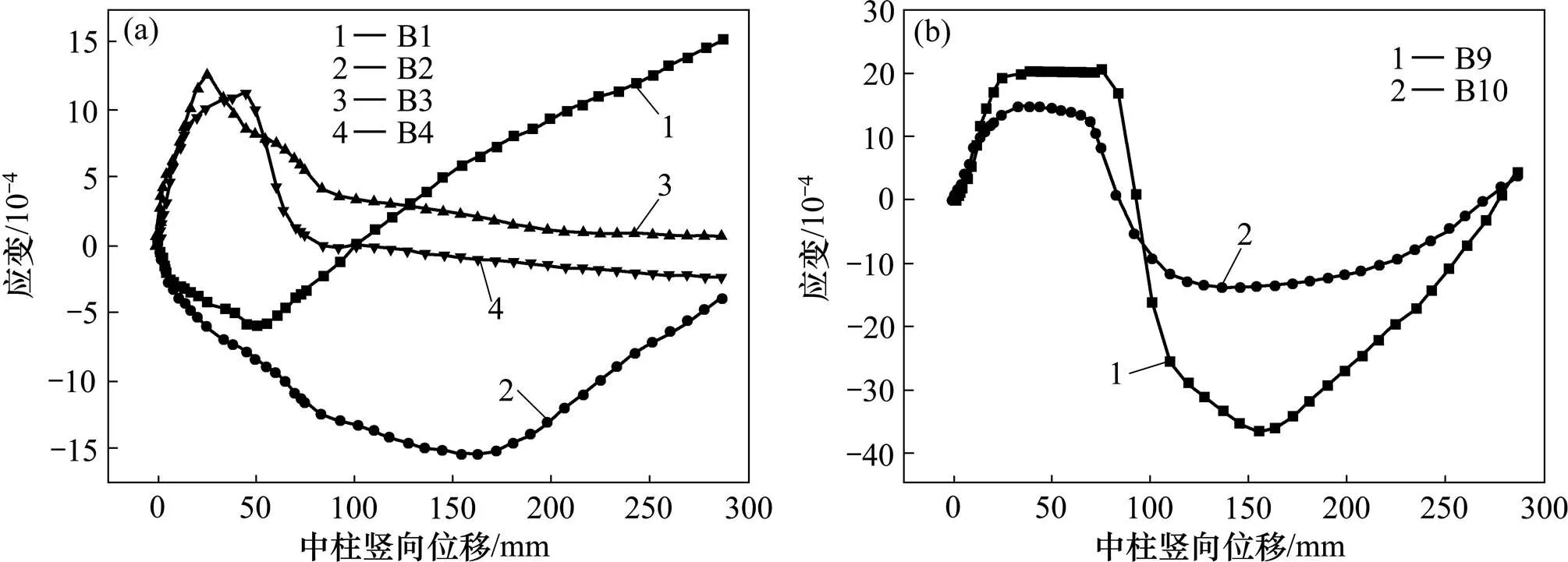
(a) 梁端截面；(b) 跨中截面

對于K1框架(見圖9)，梁端頂部鋼筋(B3和B4)在加載初期承受拉應力，隨著框架梁進入受壓混凝土破壞階段（中柱豎向位移為45 mm），梁端頂部鋼筋先后達到拉應變峰值。由于梁端截面受到預應力產生的軸向壓力的影響，隨著梁軸向壓力逐漸增大，頂部鋼筋(B3和B4)的拉應變逐漸減小，其中B4最終變為壓應變。梁端底部鋼筋(B1和B2)在加載初期承受壓應變并逐漸增大。由于軸向壓力達到壓力峰值后開始減小(這一點通過圖6也可以看出)，受其影響，梁端底部鋼筋B1和B2壓應變在達到峰值后也開始減小，其中B1壓應變變為拉應變。值得注意的是，由于試驗過程中中柱的側向支撐未起到作用，導致框架發生平面外轉動，使得B1和B2鋼筋應變有較大差別。跨中截面底部鋼筋(B9和B10)在加載初期承受拉力，且隨著豎向位移的增大而增大。受軸向壓力的影響，B9和B10鋼筋拉應變逐漸減小，并轉變為壓應變，且B9鋼筋達到屈服。隨著軸向壓力開始減小，B9和B10鋼筋應變也開始向拉應變轉變，進入懸鏈線受力階段。值得注意的是，由于試驗過程中中柱的側向支撐未起到作用，導致框架發生平面外轉動，使得B1和B2鋼筋應變有較大差別。

3 體外預應力鋼筋混凝土框架受力過程分析

3.1 壓拱階段

在荷載逐漸增加的過程中，體外預應力鋼筋混凝土梁受拉區開裂后，受拉區預應力鋼筋和非預應力鋼筋將進入明顯塑性變形或屈服狀態，受壓區邊緣混凝土應變快速增大、受壓區混凝土塑性變形發展，最終受壓區邊緣混凝土的應變將達到極限壓應變，混凝土壓碎。當荷載達到峰值u時，梁端截面達到極限彎矩u，此時梁截面進入完全塑形狀態，梁端形成塑性鉸。當框架所有梁端均形成塑形鉸后，結構轉變為幾何可變機構。采用結構塑性分析方法，可得

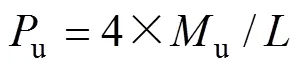
式中：為框架梁的凈跨，取為2.16 m。因此，問題的關鍵是求解截面的極限彎矩u。

體外預應力框架梁截面的應變和應力分布如圖10所示。根據圖10中的框梁受力狀態可以建立如下2個靜力平均方程。

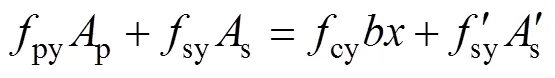
2) 對受拉區鋼筋(預應力和非預應力筋)合力作用點力矩平衡條件：

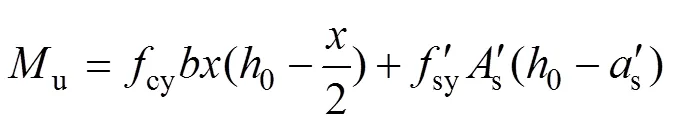
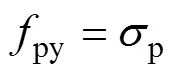
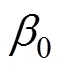
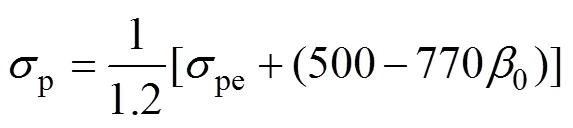
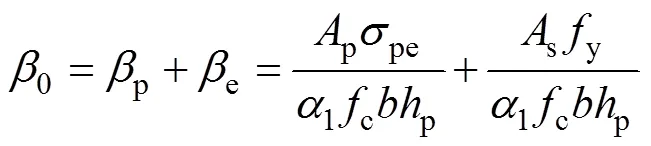
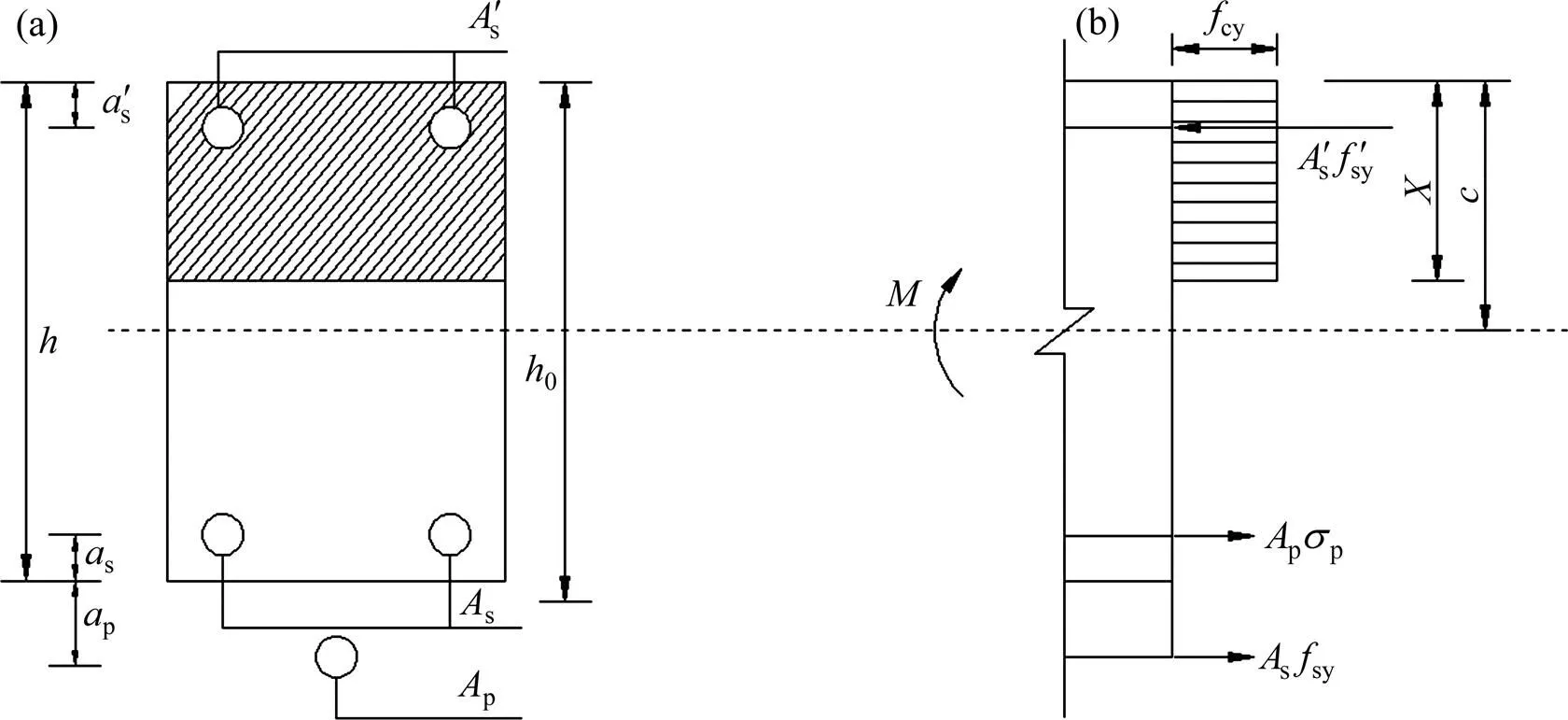
(a) 截面計算簡圖；(b) 截面應力應變分布

3.2 懸鏈線階段

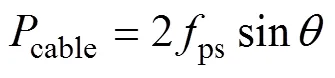
前期研究表明，無論是連續梁還是框架，構件破壞時，體外預應力筋的極限應力均未達到其屈服強度；體外預應力筋的應力增量與跨中撓度密切相關，并基本呈正比關系。因此，可以通過直接分析構件破壞時的極限撓度來確定體外預應力筋的極限應力。

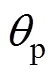
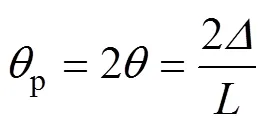
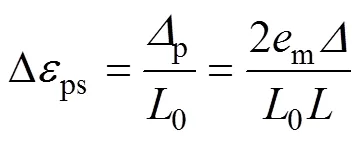
假定體外預應力筋仍處于線彈性階段，則體外預應力筋的極限應力可表示為

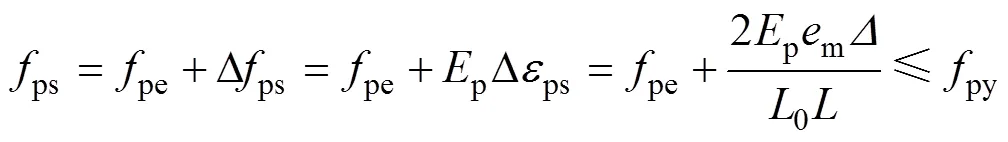
4 結論

1) 體外預應力鋼筋混凝土結構倒塌過程中，經歷了彈性階段、彈塑性階段、受壓混凝土破壞階段和懸鏈線作用階段。結構主要通過壓拱機制和懸鏈線機制進行內力重分配。懸鏈線機制提供的抗力由側向約束的剛度和強度決定，當柱對梁提供的水平約束不足時，框架的倒塌抗力隨豎向位移的增大而不斷下降。

2) 體外預應力筋可提高框架的開裂荷載、壓拱作用階段的峰值荷載以及懸鏈線作用階段的極限荷載。

3) 提出了體外預應力鋼筋混凝土框架結構倒塌破壞的極限荷載簡化計算公式，可用來預估壓拱階段及懸鏈線階段的倒塌抗力。

[1] HMSO 1976-1-102, Statutory instrument 1976, No.1676, Building and buildings[S].

[2] OPDM 2004-1-81, The building regulations 2000, Part A, schedule 1: A3, Disproportionate collapse[S].

[3] BS 8110-1-1997, Structural use of concrete, Part 1: code of practice for design and construction[S].

[4] BSEN 1992-1-1, Eurocode 2: Design of concrete structures, Part 1: General rules and rules for buildings[S].

[5] BSEN 1991-1-7, Eurocode 1: Actions on structures, Part 1-7: General actions-accidental actions[S].

[6] ACI 2008-1-479, Building code requirement for structural concrete and commentary[S].

[7] ASCE 7-05, Minimum design loads for buildings and other structures[S].

[8] GSA, Progressive collapse analysis and design guidelines for new federal office buildings and major modernization projects[S].

[9] United States Department of Defense, Unified facilities criteria design of buildings to resist progressive collapse[S].

[10] 何慶峰, 易偉建. 考慮懸索作用鋼筋混凝土梁柱子結構抗倒塌性能試驗研究[J]. 土木工程學報, 2011, 44(4): 52?59.HE Qingfeng, YI Weijian. Experimental study of the collapse-resistant behavior of RC beam-column sub-structures considering catenary action[J]. China Civil Engineering Journal, 2011, 44(4): 52?59.

[11] KHANDELWAL K, EL-TAWIL S. Catenary action during collapse of steel MRF buildings[C]// Proceedings of the 2006 Structural Engineering and Public Safety. St. Louis, USA: American Society of Civil Engineers, 2006: 1?9.

[12] ASTANEH A. Progressive collapse prevention in new and existing buildings[C]// Proceedings of the 9th Arab Structural Engineering Conference. Abu Dhabi, UAE: UAE University Publication, 2003: 1?8.

[13] YI Weijian, HE Qingfeng, XIAO Yan, et al. Experimental study on progressive collapse-resistant behavior of reinforced concrete frame structure[J]. ACI Structural Journal, 2008, 105(4): 433?439.

[14] STINGER S M, ORTON S L. Experimental evaluation of disproportionate collapse resistance in reinforced concrete frames[J]. ACI Structural Journal, 2013, 110(3): 521?530.

[15] 李鳳武, 肖巖, 趙禹斌, 等. 鋼筋混凝土框架邊柱突然失效模擬試驗與分析研究[J]. 土木工程學報, 2014, 47(4): 9?18. LI Fengwu, XIAO Yan, ZHAO Yubin, et al. Experimental and analytical study on progressive collapse of RC frame with sudden side column removal[J]. China Civil Engineering Journal, 2014, 47(4): 9?18.

[16] XIAO Yan, KUNNATH S, LI Fengwu, et al. Collapse test of three-story half-scale reinforced concrete frame building[J]. ACI Structural Journal, 2015, 112(4): 429?438.

[17] 王浩, 李易, 陸新征, 等. 單層鋼筋混凝土框架結構水平向連續倒塌試驗研究[J]. 建筑結構學報, 2016, 37(10): 65?72. WANG Hao, LI Yi, LU Xinzheng, et al. Experimental investigation on horizontal progressive collapse of one-story reinforced concrete frame[J]. Journal of Building Structures, 2016, 37(10): 65?72.

[18] 初明進, 周育瀧, 陸新征, 等. 鋼筋混凝土單向梁板子結構抗連續倒塌試驗研究[J]. 土木工程學報, 2016, 49(2): 31?40. CHU Mingjin, ZHOU Yulong, LU Xinzheng, et al. An experimental study on one-way reinforced concrete beam-slab substructures for resisting progressive collapse[J]. China Civil Engineering Journal, 2016, 49(2): 31?40.

[19] 周育瀧, 李易, 陸新征, 等. 鋼筋混凝土框架抗連續倒塌的壓拱機制分析模型[J]. 工程力學, 2016, 33(4): 34?42. ZHOU Yulong, LI Yi, LU Xinzheng, et al. An analytical model of compressive arch action of reinforced concrete frames to resist progressive collapse[J]. Engineering Mechanics, 2016, 33(4): 34?42.

[20] HOU Jian, SONG Li, LIU Huanhuan. Testing and analysis on progressive collapse-resistance behavior of RC frame substructures under a side column removal scenario[J]. Journal of Performance of Constructed Facilities (ASCE), 2015, 30(5): 04016022.

[21] HOU Jian, SONG Li. Progressive collapse resistance of RC frames under a side column removal scenario: the mechanism explained[J]. International Journal of Concrete Structures and Materials, 2016, 10(2): 237?247.

(編輯 伍錦花)

Experimental study on collapse performance of one-story reinforced concrete frames using external prestressing tendons

FAN Yunlei, WANG Jie, WANG Haolei

(College of Civil Engineering and Mechanics, Central South University of Forestry and Technology, Changsha 410018, China)

Experimental study of two single-story two-span reinforced concrete (RC) frames using external prestressing tendons was carried out to study the collapse behavior after middle-column loss. The applied load process of model frame was analyzed. A method for analyzing variation of external prestressing tendon stresses based on the structural deformation was proposed and the formula for calculating ultimate load of RC frames using external prestressing tendons was derived. The results show that progressive collapse of RC frames using external prestressing tendons after middle column loss involves four stages, i.e., elastic stage, elastic-plastic stage, compression concrete damage stage and catenary stage, in which the structure sustains and redistributes loads through the mechanism of hinge action and catenary action. Collapse resistance of RC frames with external prestressing tendons under catenary mechanism is mainly determined by the stiffness and strength of the horizontal restraint of the column. When restraint is weak, collapse resistance of RC frames with external prestressing tendons decreases with the increase of vertical displacement. External prestressing tendons improve cracking load, the peak load in arch stage and ultimate load in catenary stage of RC frames. The calculated results from the proposed formula is in good agreement with the test results, indicating that the formula can be used to estimate ultimate bearing capacity of the catenary action.

RC frames using external prestressing tendons; progressive collapse; static test; catenary action; prestressing

10.11817/j.issn.1672-7207.2018.05.028

TU375；TU378

A

1672?7207(2018)05?1244?10

2017?05?17；

2017?06?29

國家自然科學基金資助項目(51308556) ( Project (51308556) supported by the National Natural Science Foundation of China)

范云蕾，博士，副教授，從事結構抗震及抗倒塌研究；E-mail: fanyunlei@163.com