基于小波濾波的JPDA算法多目標跟蹤

莫 然, 高淑芝

(沈陽化工大學 信息工程學院， 遼寧 沈陽 110142)

由于飛行器的數據受到不同因素干擾的影響，雷達測量中目標的狀態參量測量值和目標的實際狀態參量有所不同，且跟蹤系統具有動態滯后誤差，因此如果要求既降低動態滯后的誤差又抑制其中的隨機誤差，此為增加激光雷達目標的跟蹤系統中一個重要問題.在多機動目標跟蹤的系統中融入數據小波濾波處理，能有效解決動態滯后誤差和干擾誤差一起減小的問題.小波濾波可將多種不同頻率組成的信號分解到不同的頻率區間上.

目標跟蹤是指人們使用多種觀測、計算的手段，實現對關注的運動目標進行空間狀態建模、航線估計和軌跡跟蹤的過程，它主要的任務是在復雜空中環境下檢測機動目標，并實時估計出目標的運動參數.隨著現代航空業、航海業、航天事業不斷的蓬勃發展以及現代戰爭的信息化、網絡化的發展，空中機動目標的跟蹤技術越來越受到各國的重視，目前已經成為一個極其活躍的研究領域.

在正常情況下，空中機動目標的跟蹤方法可以概括分為以下幾類：具有空中目標機動檢測的普通跟蹤算法與不需要空中機動目標檢測自適應的跟蹤算法.控制空中機動目標的跟蹤算法應該綜合運用的數學方法包括：統計決策、濾波算法等.系統將雷達傳感器中收到的信號集進行數據處理，得到機動目標的三維坐標(x,y,z)、瞬時速度(v)和瞬時加速度(a)等估計信息.空中目標跟蹤算法的原理如圖1所示.

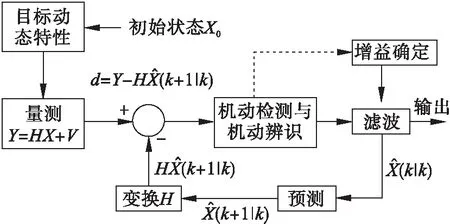
圖1 空中目標跟蹤算法原理Fig.1 The air target tracking algorithm schematic diagram

對于空中機動目標的跟蹤算法，其主要挑戰有兩種離散的未知性：對飛行目標進行跟蹤起始位置的不確定性和飛行目標軌跡運動的不確定性.跟蹤的起始位置的不確定性是指在雷達系統傳感器量測的數據很有可能是多種因素干擾的數據，其干擾因素可能是一些雜波、附近飛行目標和蓄意的飛行目標而引起的，還有可能是敵方空中目標的電子對抗系統蓄意發出的虛假信號.

文獻[1-2]提出了概率聯合數據關聯(Joint Probabilistic DataAssoci-ation,JPDA) ，它是一種能分離識別出多目標跟蹤的算法.JPDA方法是在僅適用于單目標跟蹤的概率數據關聯(Probabilistic Data Association,PDA) 方法的基礎上提出的.JPDA算法根據落入機動目標跟蹤波門內的全部點跡的不同排列形式進行聯合假設,計算這些點跡屬于機動目標的聯合概率.聯合假設的數目隨落入的跟蹤波門內全部點跡數目的上升而呈指數的增加.JPDA和PDA都是面向目標的關聯算法,這種面向目標的特征不允許在算法的框架內考慮新目標航跡起始.而在復雜的多目標跟蹤場景下,可能有新的目標出現,以及已有的某些目標的航跡終止,這種情況下,JPDA算法就必須補充特殊的邏輯.本文的重點是應用小波濾波結合JPAD算法進行多目標運動的機動分析以及對其進行跟蹤的問題.

1 JPDA-Kalman Filter數據關聯

在多個目標跟蹤中，目標與回波的關聯稱為數據關聯，這是個很關鍵的問題.解決空中目標的跟蹤中數據關聯問題即解決當前目標與回波關聯的問題.數據關聯中有3種比較典型的方法[1]：

(1) 面向空中目標的關聯方法，其考慮所有觀測值是來自于一個已知的機動目標還是雜波.

(2) 面向雷達測量值的關聯方法，其考慮所有測量值是來自于一個已知的機動目標，或是來自于一個新目標，或是雜波.

(3) 面向目標航跡的關聯方法，其考慮每條目標航跡是沒有檢測到，還是終止機動，或是和另一個測量值關聯，或預示空中目標開始機動.

1.1 PDA關聯算法

PDA是一種雜波中跟蹤單目標的有效關聯算法，它考慮了落入相關波門內的所有候選回波，并根據不同的相關情況計算出各回波來自目標的概率，然后利用這些概率值對相關波門內不同的回波進行加權，各個候選回波加權的和作為等效回波，并用等效回波對目標的狀態進行更新.利用PDA對雜波環境下的單目標進行跟蹤的優點是誤跟和丟失目標的概率較小，而且計算量小.但是若將PDA直接應用于多目標的跟蹤，由于算法沒有考慮多個目標之間的相互影響，當同時跟蹤的多個目標之間相距較近時，直接的PDA算法跟蹤性能不太理想，甚至會引起航跡的聚合[2-3].

1.2 JPDA的數學模型

JPDA算法是一種高效多目標的跟蹤關聯算法，對比于PDA算法，對多目標跟蹤的響應速度以及準確性有較大提高.JPDA在計算目標與回波的關聯概率時，用多個候選的回波分配變為一個整體回波來考慮.JPDA對當前可能的關聯解不斷進行搜索，在這種搜索的情況下，JPDA算法才可以計算出更接近于真實目標情況的后驗概率.但JPDA算法關聯求解的計算程度隨機動目標與回波數的增長而呈指數式上升，由此造成在目標跟蹤時數據處理的滯后性[4].

考慮多目標在相交區域內的多組回波對跟蹤的影響，在計算目標公共的回波的概率時，不僅要考慮候選回波距離關聯門中心大小，還要考慮關聯門內候選的回波數目影響.建模過程如下：

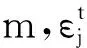
(1)

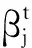
(2)

(2) 按照步驟(1)，逐次計算全部可靠航跡(目標)點跡的關聯概率.建立(m+1，n)維的概率關聯矩陣P.其中n是目標數，m是候選的回波數，j=0是該回波的雜波[6].

t=1 2 …n(目標號)

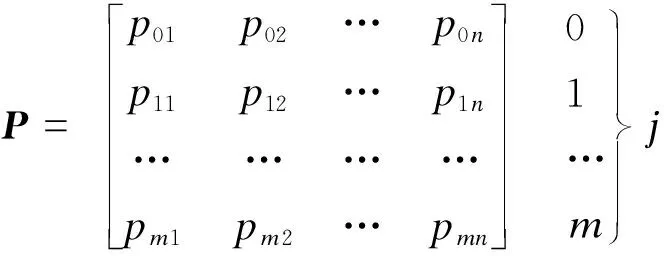
(3)

(3) 對矩陣P的每一行都進行歸一化處理，得到修正后的矩陣M：

(4)

(4) 對經過公共的回波進行加權校正后，矩陣M的每一列都進行歸一化處理，得到最后的概率K矩陣：

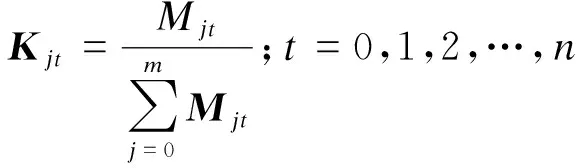
(5)

(5) 基于Kjt對全部候選的回波進行加權處理以更新機動目標的狀態.

(6)

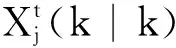
1.3 雷達站本地直角坐標系轉換至地心直角坐標系

先以地心直角坐標系為跟蹤系統統一坐標系再進行雷達數據處理中的信號坐標轉換,經雷達本地直角坐標變換為地心直角坐標,最后由地心直角坐標變換為數據處理中心的直角坐標.

假設目標在A雷達站直角坐標系所在的坐標為(x1,y1,z1),其在地心直角坐標系所在的坐標為(xe,ye,ze).當中需要進行坐標轉換,其轉換公式為[4]：

(7)

式中RT是由A雷達站本地直角坐標轉換到地心直角坐標的旋轉矩陣，如下

(8)

2 融合小波濾波

2.1 小波濾波

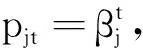
(9)

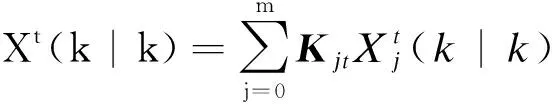
定義2：設γj是小波函數，Xt(k|k)按式(6)給出，其中f(t)∈L2(R),f(t)連續的小波變換可定義為：

Wf(a,b)=〈f,ψa,b〉=

(10)

式中：f(t)對應于當前信號，類似于用鏡頭對于機動目標進行平行動作；ψ(t)代表鏡頭中的作用，b等同于使鏡頭對于機動目標做平行動作，a的作用也同鏡頭向機動目標推進或遠離動作.當a比較大時，界面寬使得分析頻率較低，可以使其做平滑的部分界面觀察；當a比較小時，界面窄而且分析頻率較高，可以使其對細節進行界面觀察.

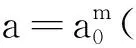
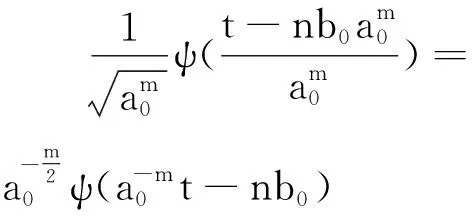
(11)

為方便計算機軟件實現，需對目標平移時間進行數據離散化，并且要求小波函數生成的小波作為標準正交基.當選擇a0=2,b0=1，則式(11)變為二進制的離散小波[5]：

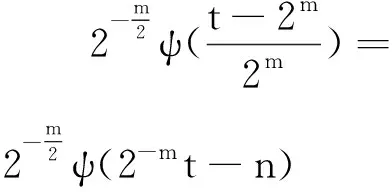
(12)

相對應的離散小波變換(簡稱：小波變換)如下：

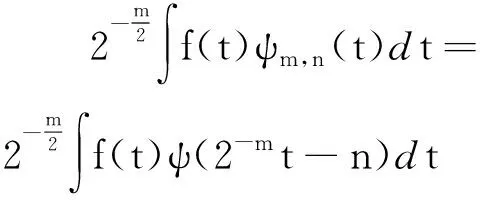
(13)

信號離散的小波變換可拆分為用低通及帶通濾波器將目標信號分解為低頻部分(表示為平滑部分)和高頻部分(表示為細節部分).它們分別反映了目標信號的概貌與細節，相似的過程可對每次分解后低頻的部分再次重復進行.按照上述的分解規律將目標信號進行小波變換，得到結果可理解成信號通過一套中心頻率不相同的帶通濾波器組份與帶寬不相同的低通濾波器的處理.

2.2 仿真平臺小波濾波算法

通過對目標地心直角坐標系坐標的濾波，得到連續曲線，其中對x軸處理程序如下：

[C,L]=wavedec(x,4,′db5′);

x=wrcoef(′a′,C,L,′db5′,4);

通過對目標地心直角坐標系坐標的濾波，得到連續曲線，其中對y軸處理程序如下：

[C,L]=wavedec(y,4,′db5′);

y=wrcoef(′a′,C,L,′db5′,4);

通過對目標地心直角坐標系坐標的濾波，得到連續曲線，其中對z軸處理程序如下：

[C,L]=wavedec(z,4,′db5′);

z=wrcoef(′a′,C,L,′db5′,4);

將3組數據再次進行融合，導入數據庫中.

2.3 分離航跡仿真

首先將數據導入Matlab中，初始未處理數據如圖2所示.

圖2 數據中2個目標的三維飛行軌跡(未分離)Fig.2 Data in two dimensional target trajectory(unsaturated)

按照JPDA方法進行數據關聯處理，分離后，未進行融合濾波的兩個目標飛行航跡如圖3所示，再用小波濾波進行處理.其中z軸方向的航跡用擬合工具得出，兩個目標飛行航跡如圖4所示.

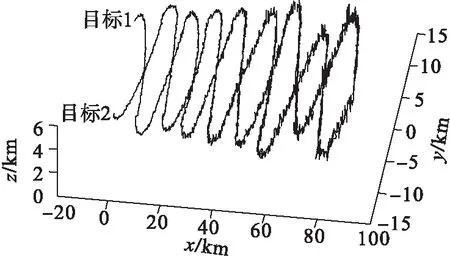
圖3 數據中2個目標的三維飛行軌跡(JPDA)Fig.3 Data in three-dimensional flight trajectory 2 goals(JPDA)

將分離后的數據進行拆分，單一進行模擬航跡，如圖5和圖6所示.未加入小波的JPDA分離數據如圖7、圖8所示.

通過仿真平臺可以看出，在仿真平臺中，利用小波濾波與JPDA算法融合的方法可有效的建立多個機動目標跟蹤系統，對數據進行處理，得到多個目標同時連續穩定的測量信號，相比于傳統JPDA算法分離，數據更加準確，減小機動目標的白噪聲，飛行軌跡清楚明了.

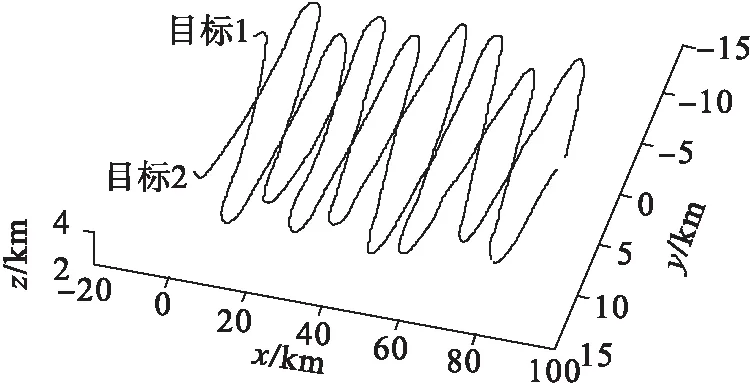
圖4 數據中2個目標的三維飛行軌跡(融合小波)Fig.4 Data in three-dimensional flight trajectory 2 goals(fusion wavelet filter)

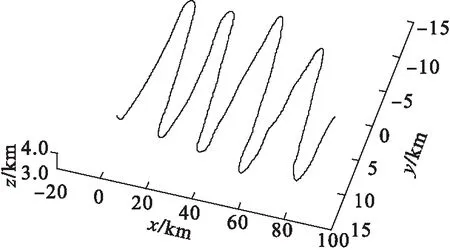
圖5 第1個目標的三維飛行軌跡Fig.5 3D flight trajectory of first goal

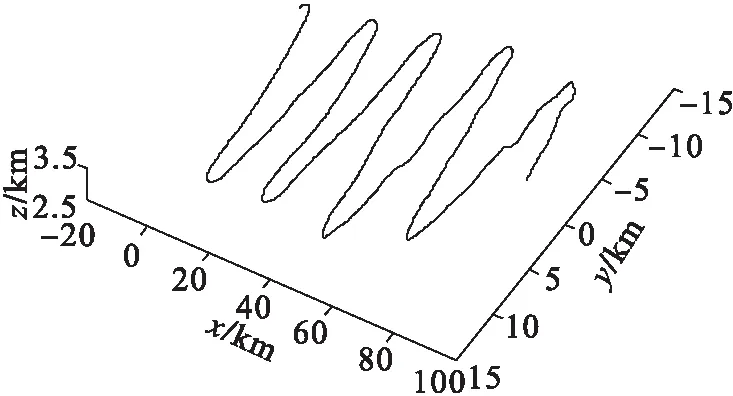
圖6 第2個目標的三維飛行軌跡Fig.6 3D flight trajectory of second goal

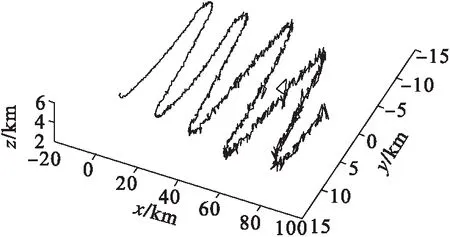
圖7 第1個目標的三維飛行軌跡(對比)Fig.7 3D flight trajectory of first goal(comparison)

圖8 第2個目標的三維飛行軌跡(對比)Fig.8 3D flight trajectory of second goal(comparison)

3 結束語

本文研究基于小波濾波與JPDA算法融合的多機動目標跟蹤模型.在進行多目標數據分離后，仿真結果表明，小波濾波能夠去除機動目標的白噪聲，JPDA算法與小波的融合可有效跟蹤多機動目標.其中，小波濾波算法比較簡單，因為每一維的小波濾波分解后目標數據量減少為原來的一半，故全部計算量最多僅為傳統濾波算法的一半(如Kalman Filter)，而且其濾波的精度和速度比傳統的算法高.雖然將小波濾波變換進一步與現有的一些先進機動目標跟蹤模型結合得到了更好的效果，但仍有不足，有待繼續研究.

：

[1] BAR-SHALOM Y,FORTMANN T E.Tracking and Data Association[M]New York:Academic Press,1988.

[2] 趙艷麗,林輝,趙鋒,等.多目標跟蹤中的數據關聯和航跡管理[J].現代雷達，2007,29(3):28-31.

[3] FORTMANN T,BAR-SHALOM Y,SCHEFFE M.Sonar Tracking of Multiple Targets Using Joint Probabilistic Data Association[J].IEEE Journal of Oceanic Engineering,1983,8(3):173-183.

[4] LI X R,JILKOV V P.A Survey of Maneuvering Target Tracking——Part Ⅳ:Decision-based Methods[C]//Proceedings of the 2002 SPIE Conference on Signal and Data Processing of Small Targets.Orleans:[s.n.],2002:4728-4760.

[5] FORTMANN T,BAR-SHALOM Y,SCHEFFE M.Sonar Tracking of Multiple Targets Using Joint Probabilistic Data Association[J].IEEE Journal of Oceanic Engineering,1983,8(3):173-184.

[6] SINHA A,DING Z,KIRUBARAJAN T,et al.Track Quality Based Multitarget Tracking Approach for Global Nearest-Neighbor Association[J].IEEE Transactions on Aerospace and Electronic Systems,2012,48(2):1179-1191.

[7] 李鋒,金宏斌,馬建朝.多雷達數據處理中坐標轉換的新方法[J].微計算機信息,2007,23(4):303-305.

[8] 王洪剛,韓文秀.基于MATLAB小波工具箱的開發與應用[J].微型機與應用，2002,21(5):52-54.