遭受DoS攻擊的短時延網絡控制系統保性能控制
何 勝 權, 俞 立
( 浙江工業大學 信息工程學院, 浙江 杭州 310023 )
0 引 言
網絡控制系統(networked control systems,NCS)由控制對象、傳感器、控制器、執行器和通信網絡組成.NCS由于具備布線靈活、安裝方便和維護費用低等優勢,在控制領域的作用越來越明顯,例如,在移動傳感器網絡[1]、無人機控制[2]、車輛自主編隊[3]等領域廣泛存在.NCS傳感器與控制器、控制器與執行器之間的數據傳輸是通過通信網絡來完成的,因此NCS與傳統控制系統最主要的區別就在于數據傳輸方式的不同.正是由于NCS的這一數據傳輸特點,其不可避免地存在著網絡誘導時延[4]、數據包丟失[5]等問題,其中又以網絡短時延問題最為常見.因此,本文主要針對包含短時延的NCS進行研究.
隨著互聯網技術快速發展,NCS的可移動性和可移植性得到了極大的提升.同時,互聯網技術更深層次的發展,給NCS共享網絡的安全性帶來了新的挑戰.網絡技術的發展打破了原有控制系統的封閉性,而且隨著TCP/IP(或UCP/IP)協議[6]商業標準化的形成,無形中也增加了NCS受到外界攻擊的概率.由此可見,NCS的安全性問題日益突出.如2012年5月底,破壞力巨大的“火焰”(flame)病毒在中東地區廣泛傳播,對伊朗等中東國家的能源工業進行猛烈攻擊,嚴重影響了這些國家一些重要能源控制系統的正常運行[7].近年來,類似的網絡攻擊事件層出不窮,由此可見,針對NCS的安全性問題展開研究尤為重要.
當然,盡管在NCS中網絡攻擊的形式日益多樣化,但其中還是有幾種比較典型的網絡攻擊形式,如DoS(Denial-of-Service)攻擊[8]、欺騙攻擊[9]等.本文主要針對在實際中攻擊范圍最廣、最容易實現的DoS攻擊進行研究.DoS攻擊即拒絕服務攻擊,該攻擊作用于NCS的共享網絡,直接導致的后果是:在DoS攻擊過程中,NCS的控制器或執行器無法接收到測量信息或控制信息,因此,對實時性要求高的系統來說,不僅會降低系統的性能,還可能造成系統的不穩定.文獻[10]提出了一種JDL數據融合模型框架,在該框架下通過主從博弈來描述不同網絡層數據間的關系,并研究了DoS攻擊的彈性控制.文獻[11]針對DoS攻擊,系統性地設計了基于輸出的動態事件觸發控制(event-triggered control,ETC)系統,該ETC策略可以保證系統的性能和魯棒性,使系統和DoS攻擊在通信資源的使用上達到平衡.文獻[12]給出了一般的控制系統在欺騙攻擊和DoS攻擊下的估計問題,但未針對NCS,特別是具有短時延的NCS.而對NCS分析的文獻,多數僅考慮網絡時延、數據包丟失等經典問題的影響.
基于此,本文同時考慮短時延和DoS攻擊問題對NCS性能的影響,主要針對執行器的執行周期比傳感器的采樣周期更快的這一類NCS[13-14],同時,把該類NCS的短時延和DoS攻擊問題統一建模成離散切換系統模型[15],并在給定的保性能指標下,設計該NCS的保性能控制器.最后通過仿真示例驗證本文結果的有效性.
1 問題描述與建模
1.1 問題描述
考慮如下連續LTI系統:

(1)
其中x(t)∈Rn是系統狀態,u(t)∈Rd是系統輸入,Ap與Bp分別是適當維數的狀態矩陣和輸入矩陣.
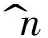



圖1 時序圖Fig.1 Timing diagram
通過定義新的采樣周期H,不僅把短時延和DoS攻擊兩個問題統一起來,還能把上述兩類DoS攻擊的情況統一起來.如圖1所示,在周期[tl,tl+1]內,同時存在u(tl-1)和u(tl)兩個輸入量,采樣周期Tsd=nT0;在周期[tl+1,tl+2]內,同時存在u(tl)和u(tl+1)兩個輸入量,采樣周期Tld=mnT0.當m=1時,兩類DoS攻擊等價,即第1類DoS攻擊是第2類DoS攻擊的特殊情況.因此,只需要分析第2類DoS攻擊對系統(1)的影響即可.
1.2 閉環系統建模
記hk∈H,k∈N,表示在[tk,tk+1]時間內的采樣周期時長,即hk=tk+1-tk.假設在采樣周期hk內執行器的兩個輸入量u(tk-1)和u(tk)的作用時間分別為n1(k)T0和n0(k)T0,且符合關系式n1(k)T0+n0(k)T0=hk=mnT0.
對系統(1)考慮DoS攻擊的影響,得到如下離散系統:
x(tk+1)=A(hk)x(tk)+B(hk)u(tk)+
B(hk-1)u(tk-1)
(2)

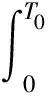
所以,系統(2)等價于
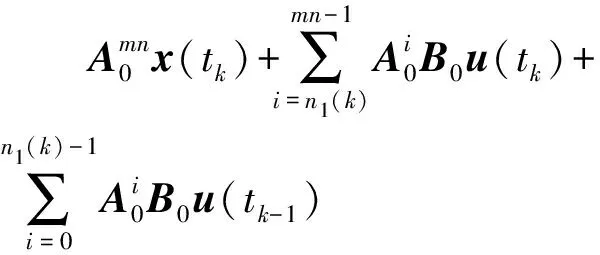
(3)


(4)

Boσ(tk)=∑mn-1i=n1(k)Ai0B0,B~oσ(tk)=∑n1(k)-1i=0Ai0B0,Aoσ(tk)=Amn0,σ(tk)∈Z
其中是切換信號.
進一步,選取反饋控制律u(tk)=Kx(tk),得到如下閉環切換系統模型:
Scσ(tk):x(tk+1)=Aσ(tk)x(tk)+Bσ(tk)x(tk-1)
(5)

離散系統(5)等價于如下描述的系統:該系統的執行周期為T0,采樣周期為n1(k)T0,n1(k)∈Z.因此,在切換信號σ(tk)的作用下,Scσ(tk)描述了該系統的狀態反饋模型.
2 穩定性分析
定義1對于給定切換信號σ(tk)和任意的tk≥1,令Nσ[t0,tk)表示切換信號σ(tk)在時間間隔[t0,tk)內的切換次數,若存在N0≥0,ta≥0,使得Nσ[t0,tk)≤N0+(tk-t0)/ta成立,那么ta稱為切換信號σ(tk)的平均駐留時間,N0稱為抖動界.

令nj表示子系統Sj在時間間隔[t0,tk)內激活的次數,j∈Z.以下定理給出了系統(5)指數穩定的一個充分條件.
定理1考慮系統(5),若存在正標量λj>0,λ<1和μ≥1,以及適當維數的矩陣Pj≥0,Qj≥0,j∈Z,使得以下不等式
(6)
Pα≤μPβ,Qα≤μQβ;α,β∈Z
(7)
(8)
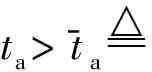
ta>t-a

(9)
成立,那么系統(5)指數穩定,并具有指數衰減率ρ(λ,ta)=λμ1/2ta.
證明系統(5)的子系統模型為
Sj:x(tk+1)=Ajx(tk)+Bjx(tk-1);j∈Z
(10)
為系統(10)選取如下Lyapunov函數:
Vj(tk)=xT(tk)Pjx(tk)+xT(tk-1)Qjx(tk-1)
記η(tk)=(xT(tk)xT(tk-1))T,則由不等式(6)可得
即可得
(11)
為系統(5)選取如下Lyapunov函數:
Vσ(tk)(tk)=xT(tk)Pσ(tk)x(tk)+xT(tk-1)Qσ(tk)x(tk-1)
對于切換信號σ(tk),令tk1<… Vσ(tki)(tki)≤μVσ(tk(i-1))(tki) (12) 由不等式(6)、(11)和(12)遞推可得 λ2tk1Vσ(t0)(t0)≤ μNσ[t0,tk)λ2tkVσ(t0)(t0)= ρ2tk(λ,ta)Vσ(t0)(t0) (13) (14) 繼而可得 (15) 此外,不等式(9)和λ<1確保了ρ(λ,ta)<1.因此,由定義2可知,系統(5)指數穩定,且具有指數衰減率ρ(λ,ta)=λμ1/2ta.證畢. 本文針對系統(5)考慮如下保性能指標: uT(tk-1)G3u(tk-1)] (16) 其中G1、G2和G3都是給定的正定常數矩陣.如果在反饋控制律u(tk)=Kx(tk)的作用下,系統(5)是指數穩定的,且性能J是有界的,滿足J≤ J- ,那么該反饋控制律就是系統(5)的保性能控制器,系統具有保性能水平 J- .下面給出一個使系統(5)指數穩定的充分條件. 定理2考慮系統(5),若存在正標量λj>0,λ<1和μ≥1,以及適當維數矩陣Pj≥0,Qj≥0,j∈Z,使得不等式(7)~(9)以及不等式 Ω~jATjBTj()Pj(Aj Bj)+Λ100Λ2()<0 (17) J-(λ,ta)=1-λ2minρ-2tk(λ,ta)-1Vσ(t0)(t0),λmin=minj∈Z{λj}. 令 J(tk)=xT(tk)G1x(tk)+uT(tk)G2u(tk)+uT(tk-1)G3u(tk-1) 與不等式(11)的推導過程類似,可得 即 (18) 對于切換信號σ(tk),令tk1<… J(tk(i-1)))-J(tki)<…< (19) 結合式(12)和(19)可遞推得到 Vσ(tk(i-1))(tk(i-1))- (20) 其中 進一步,結合式(13)和(20),且根據關系式Vσ(tk)(tk)≥0,可得 Φ(J(s))<ρ2tk(λ,ta)Vσ(t0)(t0)-Vσ(tk)(tk)≤ ρ2tk(λ,ta)Vσ(t0)(t0) (21) 又因Nσ[t0,tk-1)≥0,所以對?s∈{0,…,tk-1},可得如下關系式: (22) (23) 對式(23)左右兩邊從tk=1→+∞求和,分別得 (24) (25) 結合式(23)~(25)可得 ∑+∞s=0J(s)≤1-λ2minρ-2tk(λ,ta)-1Vσ(t0)(t0)J-(λ,ta) (26) 即時系統(5)具有保性能水平.證畢. 先給出一個在后續證明中需要用到的引理. 引理1[16]對任意矩陣A,P>0和Q>0,不等式ATQA-P<0成立,當且僅當存在一個矩陣Y,使得以下矩陣不等式成立: 緊接著,給出下面的定理.該定理通過對一個優化問題的求解,得到系統(5)的保性能控制器. 定理3考慮系統(5)和性能指標(16),若存在正標量λj>0,λ<1和μ≥1,以及適當維數的矩陣X,V,Rj≥0,Sj≥0,j∈Z,使得以下優化問題 minδ s.t. 式(8),式(9), Ω^ j<0,Ψ<0;j∈Z Rα≤μRβ,Sα≤μSβ;α,β∈Z (27) 成立,且有最小目標函數δ*.那么具有增益矩陣K=V-1X的狀態反饋控制器是一個最優反饋保性能控制器,使系統(5)指數穩定且具有指數衰減率ρ(λ,ta)和保性能水平 J- (λ,ta).其中 Ω^j-λ2Rj+Sj0XTAToj+VTBTojΔT1?-λ2jSjVTB~TojΔT2??-X-XT+Rj0???-δG?è???????÷÷÷÷÷ΔT1=(XT VT 0), ΔT2=(0 0 VT)G=diag{G-11,G-12,G-13}Ψ-IxT(t0)?-X-XT+R0(); R0∈{Rj, j∈Z} 證明定理2中的 Ω~ j<0等價于 (28) 其中Λ1=-λ2Pj+Qj+G1+KTG2K.由上式可知,矩陣Y是可逆的.定義X=δY-1,記V=KX,Rj=XTPjX/δ,Sj=XTQjX/δ,對式(28)分別左乘矩陣diag{XT,XT,XT},右乘矩陣diag{X,X,X},再應用Schur補定理即可得到不等式 Ω^ j<0. 對不等式Pα≤μPβ和Qα≤μQβ都分別左乘矩陣δ-1/2XT,右乘矩陣δ-1/2X,即可得到矩陣不等式Rα≤μRβ,Sα≤μSβ,α,β∈Z. 定義P0=Pσ(t0)∈{Pj,j∈Z},由Vσ(t0)(t0)=xT(t0)Pσ(t0)x(t0)<δ,可得 Ψ~-δIxT(t0)Y?-Y-YT+P0()<0 (29) 對式(29)分別左乘矩陣diag{δ-1/2I,δ-1/2XT},右乘矩陣diag{δ-1/2X,δ-1/2I},可得不等式Ψ<0.證畢. 考慮一個文獻[17]中簡化的實際直流電機模型,x=(θω)T是其狀態量,其中θ和ω的物理意義分別表示電機的角位置和角速度,其狀態空間模型表述如下: x.=011-217.4()x+01 669.5()u (30) 選取系統的采樣周期T=5 ms,執行周期T0=1 ms,則n=5.由此可得 假設 n^ =1,即系統的短時延總是滿足條件τ≤T0.另外,假設 M- Z^ =3,即m∈{1,2,3}.因此,設n1(k)的取值為n1(k)∈{1,6,8,10,12},即整個切換系統模型由5個子系統Sj(j∈ Z^ )組成. 選取μ=1.01,λ1=0.96,λ6=1.20,λ8=1.25,λ10=1.30,λ12=1.32,求解優化問題(27)得到一個可行的控制器增益 K=(-2.827 9 -0.014 3) 為滿足條件(8),可取λ=0.99.此時,所考慮的閉環系統總能指數穩定,并且具有指數衰減率ρ=λμ1/2=0.995. 假設在時間間隔[t0,t100)內,系統遭受DoS攻擊的情況由以下子系統切換序列 表示,則子系統S1、S6、S8、S10、S12分別發生了93、2、2、2、1次.由定理3可知,在控制器u(tk)=Kx(tk)的作用下,閉環系統指數穩定,并且具有指數衰減率ρ=0.995. 給定x(t0)=(0.5 0.2)T為系統(30)的初始狀態,仿真結果如圖2、3所示.圖2是發生DoS攻擊時刻的分布圖.圖3是DoS攻擊下的系統狀態軌跡圖,由于圖中角位移θ的狀態曲線在DoS攻擊下變化較緩,故選取其中一部分受影響的曲線(小方圈A包圍的曲線)進行放大.圖3中Ⅰ~Ⅲ反映了系統(30)在遭受DoS攻擊時系統性能的變化情況.該仿真結果說明了所設計的保性能控制器的有效性. 圖2 DoS攻擊分布Fig.2 Distribution of DoS attacks 圖3 DoS攻擊下的系統狀態軌跡Fig.3 State trajectories of the system under DoS attacks 本文同時考慮了短時延和DoS攻擊對NCS性能的影響.首先,通過重新定義采樣時間的處理方法,把NCS的短時延和兩類DoS攻擊問題統一建模成同時包含確定和不確定子系統的切換系統模型.隨后,用切換系統的分析方法,給出了本文所考慮的NCS指數穩定的充分條件.進一步,通過給出保性能控制水平,設計了系統的最優保性能控制器.最后,通過一個仿真示例驗證了所設計的保性能控制器的有效性. [1] OGREN P, FIORELLI E, LEONARD N E. Cooperative control of mobile sensor networks: Adaptive gradient climbing in a distributed environment [J].IEEETransactionsonAutomaticControl, 2004,49(8):1292-1302. [2] DING X C, POWERS M, EGERSTEDT M,etal. Executive decision support:Single-agent control of multiple UAVs [J].IEEERoboticsandAutomationMagazine, 2009,16(2):73-81. [3] ALAM A A, GATTAMI A, JOHANSSON K H. Suboptimal decentralized controller design for chain structures:Applications to vehicle formations [J].ProceedingsoftheIEEEConferenceonDecisionandControl, 2011:6160938. [4] NILSSON J, BERNHARDSSON B. Analysis of real-time control systems with time delays [J].ProceedingsoftheIEEEConferenceonDecisionandControl, 1996,3:3173-3178. [5] 朱其新. 網絡控制系統的建模、分析與控制[D]. 南京:南京航空航天大學, 2003. ZHU Qixin. Modeling, analysis and control of networked control systems [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2003. (in Chinese) [6] LAKSHMAN T V, MADHOW U. Performance of TCP/IP for networks with high bandwidth-delay products and random loss [J].IEEE/ACMTransactionsonNetworking, 1997,5(3):336-350. [7] IASIELLO E. Cyber attack:A dull tool to shape foreign policy [J].InternationalConferenceonCyberConflict,CYCON, 2013:6568392. [8] UMA M, PADMAVATHI G. A survey on various cyber attacks and their classification [J].InternationalJournalofNetworkSecurity, 2013,15(5):390-396. [9] ZHANG Heng, CHENG Peng, WU Junfeng,etal. Online deception attack against remote state estimation (IFAC-PapersOnline) [J].IFACProceedingsVolumes, 2014,19:128-133. [10] YUAN Yuan, SUN Fuchun. Data fusion-based resilient control system under DoS attacks:A game theoretic approach [J].InternationalJournalofControl,AutomationandSystems, 2015,13(3):513-520. [11] DOLK V S, TESI P, DE PERSIS C,etal. Output-based event-triggered control systems under Denial-of-Service attacks [J].ProceedingsoftheIEEEConferenceonDecisionandControl, 2015:7402972. [12] LI Y M, VOOS H, DAROUACH M. RobustH∞cyber-attacks estimation for control systems [J].Proceedingsofthe33rdChineseControlConference,CCC2014, 2014:6895451. [13] ROSHANY-YAMCHI S, CYCHOWSKI M, NEGENBORN R R,etal. Kalman filter-based distributed predictive control of large-scale multi-rate systems:Application to power networks [J].IEEETransactionsonControlSystemsTechnology, 2013,21(1):27-39. [14] ZOU Y, CHEN T, LI S. Network-based predictive control of multirate systems [J].IETControlTheoryandApplications, 2010,4(7):1145-1156. [15] 張文安. 網絡化控制系統的時延與丟包問題研究[D]. 杭州:浙江工業大學, 2010. ZHANG Wenan. Research on the delay and packet loss issues in networked control systems [D]. Hangzhou: Zhejiang University of Technology, 2010. (in Chinese) [16] BOYD S, GHAOUI L E, FERON E,etal.LinearMatrixInequalitiesinSystemandControlTheory[M]. Philadelphia: SIAM, 1994. [17] LI Hongbo, CHOW M Y, SUN Zengqi. Optimal stabilizing gain selection for networked control systems with time delays and packet losses [J].IEEETransactionsonControlSystemsTechnology, 2009,17(5):1154-1162.
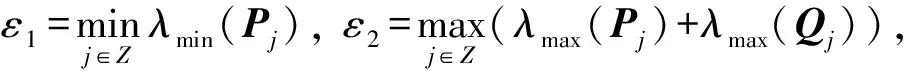
3 保性能控制器設計




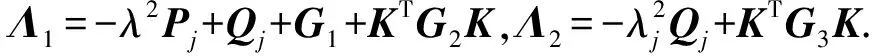





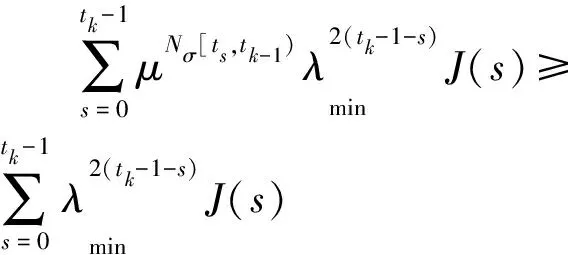
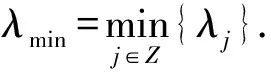





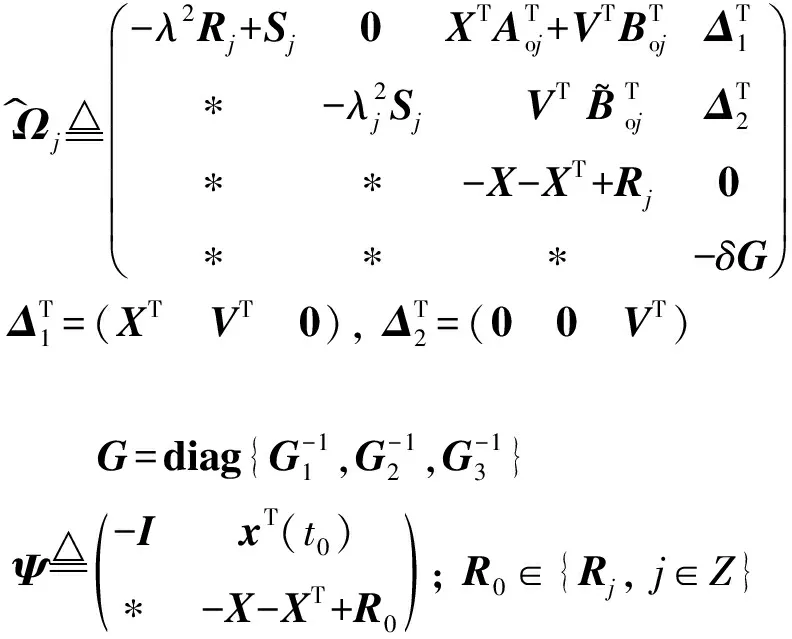



4 示 例
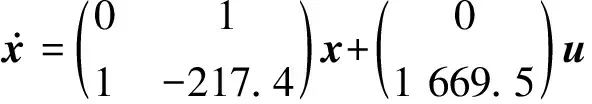
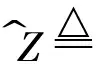


5 結 語

