微生物連續發酵過程線性反饋最優控制

貝 泓 涵， 張 立 衛， 孫 菁

( 大連理工大學 數學科學學院, 遼寧 大連 116024 )

0 引 言

1,3-丙二醇在化妝品、聚合物、膠黏劑、潤滑劑、藥物等方面有廣泛的應用[1]．目前，生產1,3-丙二醇的方法主要有兩種：化學合成和微生物發酵．相比于化學合成，微生物發酵更具有吸引力，因為過程更容易施行，并且從環保角度上來講沒有毒副產物產生．然而，由于微生物發酵法生產1,3-丙二醇相比于化學合成產量較低，目前還不能應用于工業生產上．這使得越來越多的學者聚焦于提高微生物發酵生產1,3-丙二醇的產量上[2-4]．

自20世紀80年代起就開展了對1,3-丙二醇的微生物轉化過程研究，近些年學者們對該過程的研究更為細致精確[5]．微生物發酵生產1,3-丙二醇主要有3種方式：間歇發酵、連續發酵和批式流加發酵．連續發酵是指在裝有一定體積發酵液(含有菌種和培養基)的發酵罐中，以一定速率注入具有一定濃度底物的同時以相同速率從發酵罐中取出發酵液，整個過程中保持發酵液體積不變．其具有生產強度高、產量穩定、自動化程度高的優勢，因此，本文將著眼于研究連續發酵過程．

對連續發酵過程的研究學者們已取得了一定成績．Zhang等[6]根據1,3-丙二醇跨細胞膜的可能傳輸機制提出了一種描述細胞內還原途徑的非線性混雜系統．Gao等[7]認為，甘油通過細胞膜有3種可能的途徑，其中包括1,3-丙二醇的被動擴散和主動轉運，并建立了一種改進的14維非線性混合動力系統，用遺傳調控來描述微生物的連續發酵過程．Lv等[8]在微生物連續培養過程中考慮了一種非線性不可微動態系統，包括3-羥基丙醛抑制機制對細胞生長所有可能的代謝通路，以及甘油和1,3-丙二醇在細胞膜上的輸運系統．本文將研究微生物連續發酵過程的反饋最優控制問題．

近年來，學者們提出了幾種新的求解連續不等式約束最優控制問題的計算方法，包括非光滑牛頓法[9]、約束轉錄法[10]、精確罰方法[11]、無損卷積法和基于區間分析的方法．雖然這些方法在解決實際問題上已被證明非常有效，但它們只能夠實現開環控制，這種開環控制在實踐中不能保證魯棒性．因此，在微生物連續發酵生產1,3-丙二醇的最優化問題上建立一種反饋控制策略，可以更好地保證魯棒性，并實現閉環控制．

解決最優反饋控制的傳統方法包括解決HJB偏微分方程(即使對于無約束的問題來說也是一項困難的任務)．因此，一般而言，計算約束系統的最優反饋控制是非常具有挑戰性的．盡管如此，文獻中還是有部分嘗試．在文獻[12]中，通過求解一個反饋增益為決策變量的優化問題得到了一個最優PID控制器．這個問題包含了由于控制器的工程規范而產生的連續的不等式約束，比如超調和上升時間的限制．利用約束轉錄方法文獻[13]確定了最優反饋增益，這是一種處理狀態約束的著名計算方法．解決反饋控制問題的其他相關方法包括：計算魯棒次優控制器的敏感罰方法[14-15]，以及鄰近的極值方法[16-17]——當系統的新信息可用時，調用規則來更新最優控制．文獻[18]描述了一種專門為登月模塊設計的反饋控制方法，該方法基于時間尺度和控制參數化技術的新組合[19]、著名的彭特里亞金的最小原理[20]和三次樣條逼近[21]．文獻[22]考慮了一個一般的最優控制問題，即給定結構的反饋控制器通過改變某些可調參數來優化．

本文提出一種微生物連續發酵生產1,3-丙二醇的線性反饋控制策略，建立線性反饋控制器使得1,3-丙二醇的產量最大化．

1 問題描述

根據發酵實驗過程，做出如下假設[23]：

(H1) 發酵罐中物質組成不隨空間位置變化，即反應器內各點的物質組成均一；

(H2) 連續加入的培養基只含有甘油，反應器中的培養液以稀釋速率D輸出．

在上述假設下，微生物連續發酵過程中生物質、基質和產物的質量平衡關系可以表示為如下的非線性動態系統：

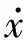
(1)

并且

xi(0)=x0i；i=1，2，3，4，5

(2)

式中：x1(t)、x2(t)、x3(t)、x4(t)和x5(t)分別表示在時刻t生物質、細胞外甘油、細胞外1,3-丙二醇、乙酸和乙醇的濃度(mmol/L)，x0i是其初始濃度(mmol/L)；t∈[0，tf]，tf是終端時刻；μ是細胞的比生長速率(h-1)；q2是底物的比消耗速率(h-1)；q3、q4、q5分別表示1,3-丙二醇、乙酸和乙醇的比生長速率(h-1)；Cs0表示注入的甘油濃度．

(3)

(4)

(5)

(6)

(7)

其中μm=0.67 h-1，是最大比生長速率；ks=0.28 mmol/L，是Monod飽和常數．

令x(t)=(x1(t)x2(t) …x5(t))T，x0=(x01x02…x05)T，u(t)∶=(DCs0)，并且，f(x(t)，u(t))∶=(f1(t) …f5(t))T．

那么非線性控制系統為

x.

x(0)=x0

(8)

考慮到實際的發酵過程中，各物質均有臨界濃度，即狀態向量是有嚴格區間的，因此，給出集合W來界定生物質、甘油以及產物的濃度區間：

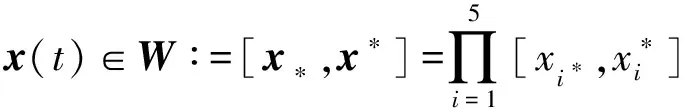
(9)

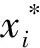
式(9)可以如下式所示等價地轉換為連續狀態不等式約束：

hi(x(t)，u(t))≤0；t∈[0，tf]，i=1，…，10

(10)

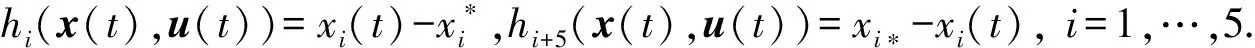
稀釋速率D以及注入的甘油濃度Cs0有相應的臨界值，因此控制變量u(t)應滿足如下約束：

u*≤u(t)≤u*；t∈[0，tf]

其中u*和u*分別為u(t)的下確界、上確界．

記x3(·|u(t))為方程(8)的解(1,3-丙二醇濃度)，那么最優化問題如下所示：

問題P0選擇u(t)使得成本函數最小化

minJ0(u)=-x3(tf|u(t))s.t.

x(t)∈W

u*≤u(t)≤u*

2 反饋控制

在甘油歧化過程中，對1,3-丙二醇最終濃度影響最大的兩個因素就是生物質和甘油的濃度，并且線性狀態反饋也是常見的反饋控制結構之一．因此，選用與生物質、甘油濃度相關的線性反饋控制器：

u(t)=(DCs0)=(φ1(x(t)，ξ)φ2(x(t)，ξ))

(11)

其中φ1(x(t)，ξ)=ξ1x1(t)+ξ2x2(t)，φ2(x(t)，ξ)=ξ3x1(t)+ξ4x2(t)；記ξ=(ξ1ξ2ξ3ξ4)T∈R4是反饋控制參數向量；φ1和φ2是如上的連續可微函數．那么，反饋參數ξ1、ξ2、ξ3、ξ4是需要最優選擇的決策變量．

反饋參數須滿足如下有界約束條件：

ξ=(ξ1ξ2ξ3ξ4)T∈Uad=

[α1，β1]×[α2，β2]×[α3，β3]×[α4，β4]

(12)

將式(11)代入式(8)中有

(13)

其中

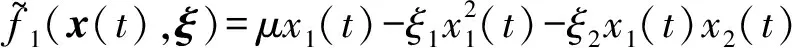
f～

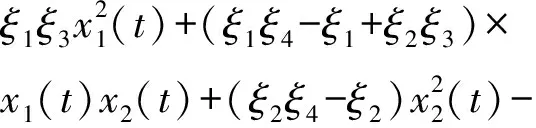
q2x2(t)

(14)

方程(14)應滿足方程(8)的初始條件，另記x(·|ξ)為方程(14)的解．此外，約束條件(10)變為

hi(x(t)|ξ)≤0；t∈[0，tf]，i=1，…，10

(15)

本文的目標是通過狀態反饋策略使1,3-丙二醇的最終濃度最大化，那么首先考慮在滿足約束條件(15)的基礎上，選擇最優反饋參數ξk(k=1，2，3，4)使得系統成本最小化．

問題P 選擇ξ∈Uad使得成本函數最小化

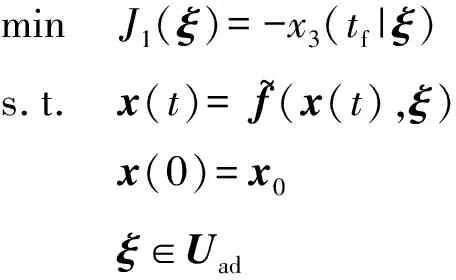
minJ1(ξ)=-x3(tf|ξ)s.t.x(t)=f～(x(t),ξ)x(0)=x0ξ∈Uad

3 精確罰方法

問題P是一個非線性優化問題，在此問題中，有限數量的決策變量(反饋控制參數)需要滿足約束條件并進行優化．這是個非常難以解決的優化問題，因為每個連續不等式約束條件實際上都是由無限個(對應時間區間[0，tf]的每個點)約束條件組成的．那么，問題P就可以看成是一個半無限優化問題．為解決這個問題，接下來使用精確罰方法[24]得到問題P的近似問題．

x(t)∈W等價于G(ξ)=0，其中

(16)

顯然G(ξ)=0當且僅當x(t)∈W．然而，等式約束條件(16)當hi=0時非光滑，因此，一般的優化程序在處理此類等式約束問題上有一定的困難．那么，考慮如下的精確罰函數：

Jσ(ξ，

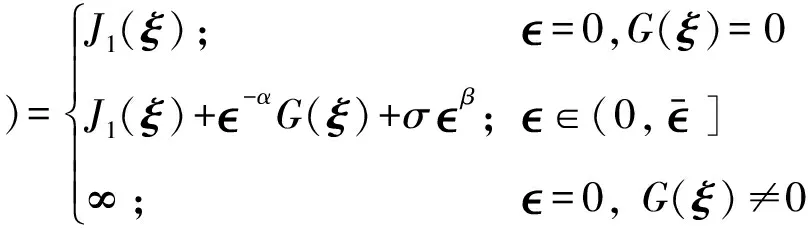
)=J1(ξ);=0,G(ξ)=0J1(ξ)+-αG(ξ)+σβ;∈(0,-]∞;=0, G(ξ)≠0ì?í????

(17)

罰函數Jσ用于懲罰G(ξ)中的較大值，因此，最小化Jσ能讓可行點滿足約束條件(15)．在此基礎上，問題P可近似于如下罰問題：

問題Q 選擇(ξ，)∈Uad×[0，]使得罰函數Jσ(ξ，)最小化．

minJσ(ξ，)=J1(ξ)+-αG(ξ)+σβs.t.x(t)=(x(t)，ξ)

x(0)=x0

ξ(t)∈Uad

解決這個問題的數值算法利用了成本函數的梯度來找到滿足搜索空間可行區域的上升方向，采用如下方法來計算成本函數的梯度：

首先，對于每個k=1，…，4，考慮如下的變分方程：

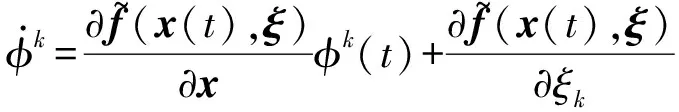
?.k=?f～(x(t),ξ)?x?k(t)+?f～(x(t),ξ)?ξk

(18)

φk(0)=0

(19)

其中

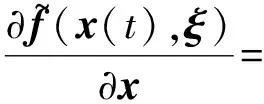
?f～(x(t),ξ)?x=

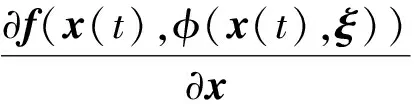
(20)

并且

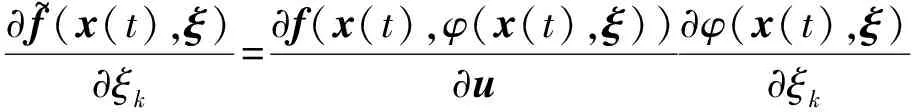
?f～(x(t),ξ)?ξk=?f(x(t),φ(x(t),ξ))?u?φ(x(t),ξ)?ξk

(21)

記φk(·|ξ)為方程(18)、(19)的解，有如下定理：

定理1對每一ξ∈Γ

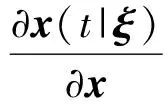
(22)

基于定理1，使用標準微分法則，可以得到Jσ的偏微分．

定理2問題Q中，Jσ的偏微分如下：

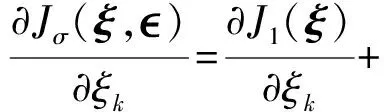
(23)

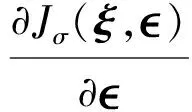
(24)

其中

(25)

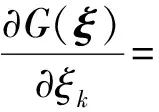
(26)

以及，Φ(x(tf|ξ))=-x3(tf|ξ)．

4 算法及數值結果

基于上述內容，給出求解問題Q的算法：

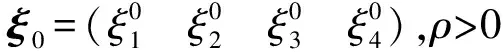
步驟2令

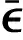
步驟3以(ξ0，0)作為初值，使用非線性優化算法二次序列規劃方法(SQP)求解問題Q．記(ξ*，*)為求得的局部最小解，其中

步驟4如果*<ρ，則停止，取ξ*作為問題Q的一個解．否則，令10σ→σ轉到步驟5．

步驟5如果σ≤σmax，那么令(ξ*，*)→(ξ0，0)并轉到步驟2．否則停止——t算法無法得到問題Q的解．

在37 ℃，pH=7．0的厭氧條件下，系統的取值如表1所示[25]．

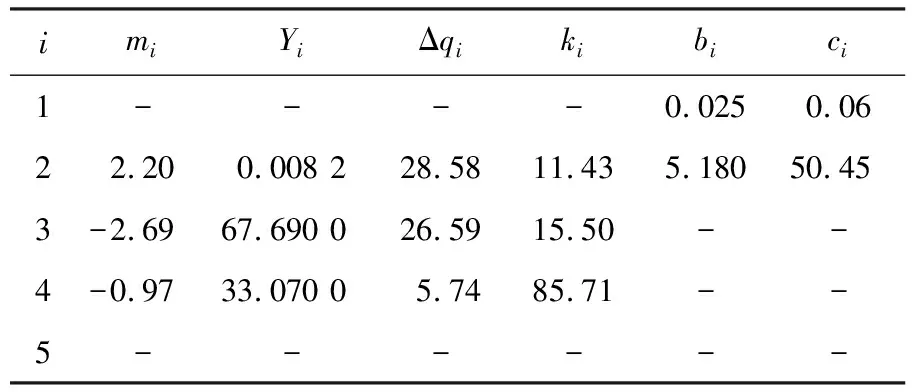
表1 參數取值

在微生物發酵過程控制中，取狀態向量的臨界值為x*=(0.001 100 0 0 0)T，x*=(10

2 039 939.5 1 026 360.9)；生物質、甘油以及1,3-丙二醇、乙酸、乙醇的初始濃度分別為x01=0.1 mmol/L，x02=400 mmol/L，x03=0，x04=0，x05=0．控制變量D、Cs0應滿足D(t)∈[0.05，0.67]，Cs0(t)∈[100，1 800]．連續發酵過程中基質充分，取反應時間為100 h.在數值實驗過程中，作為經驗數值，ξ的參數取值范圍為[0，400]×[0，2]×[0，20]×[0，0.000 1]．通過本文的算法計算得出，反饋控制最優參數ξ*=(394.132 8 0.630 4 0.085 0.000 05)，1,3-丙二醇在終端時刻的濃度為426.836 4 mmol/L．控制變量D、Cs0如圖1、2所示；生物質、甘油、1,3-丙二醇、乙酸、乙醇的濃度如圖3所示．

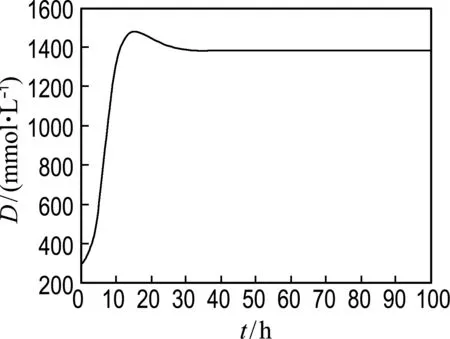
圖1 控制變量DFig.1 Control variable D

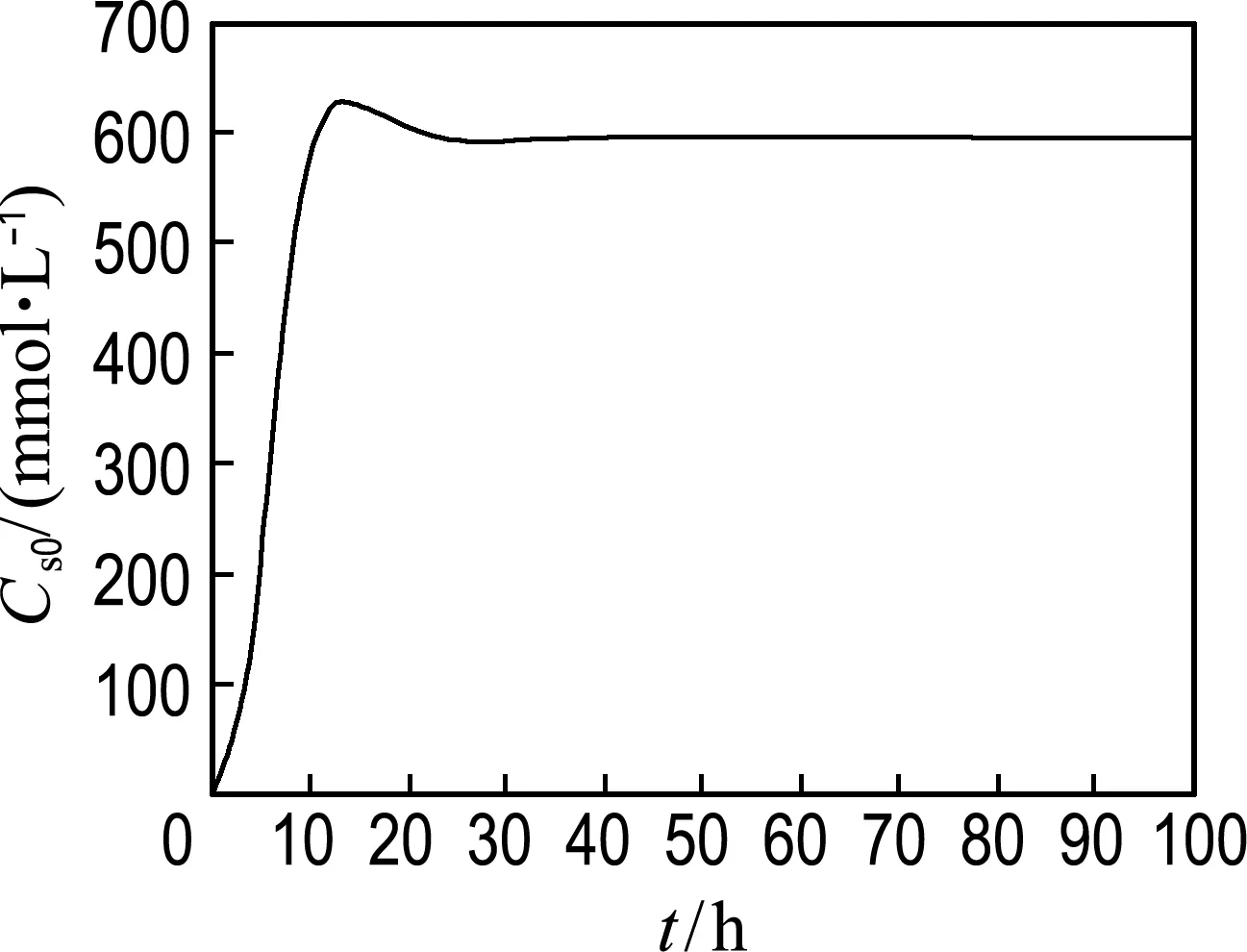
圖2 控制變量Cs0Fig.2 Control variable Cs0

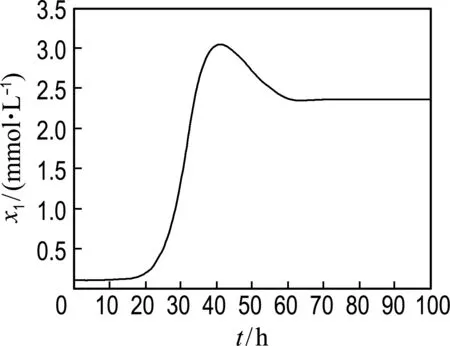
(a) 生物質

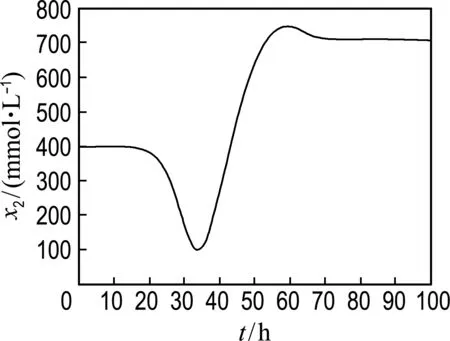
(b) 甘油

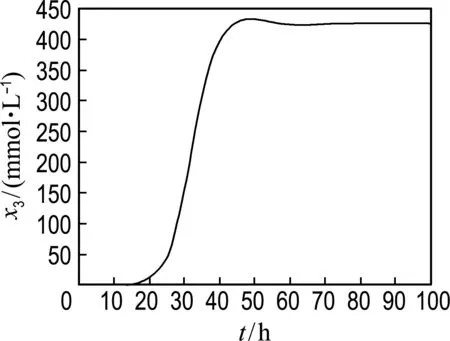
(c) 1,3-丙二醇

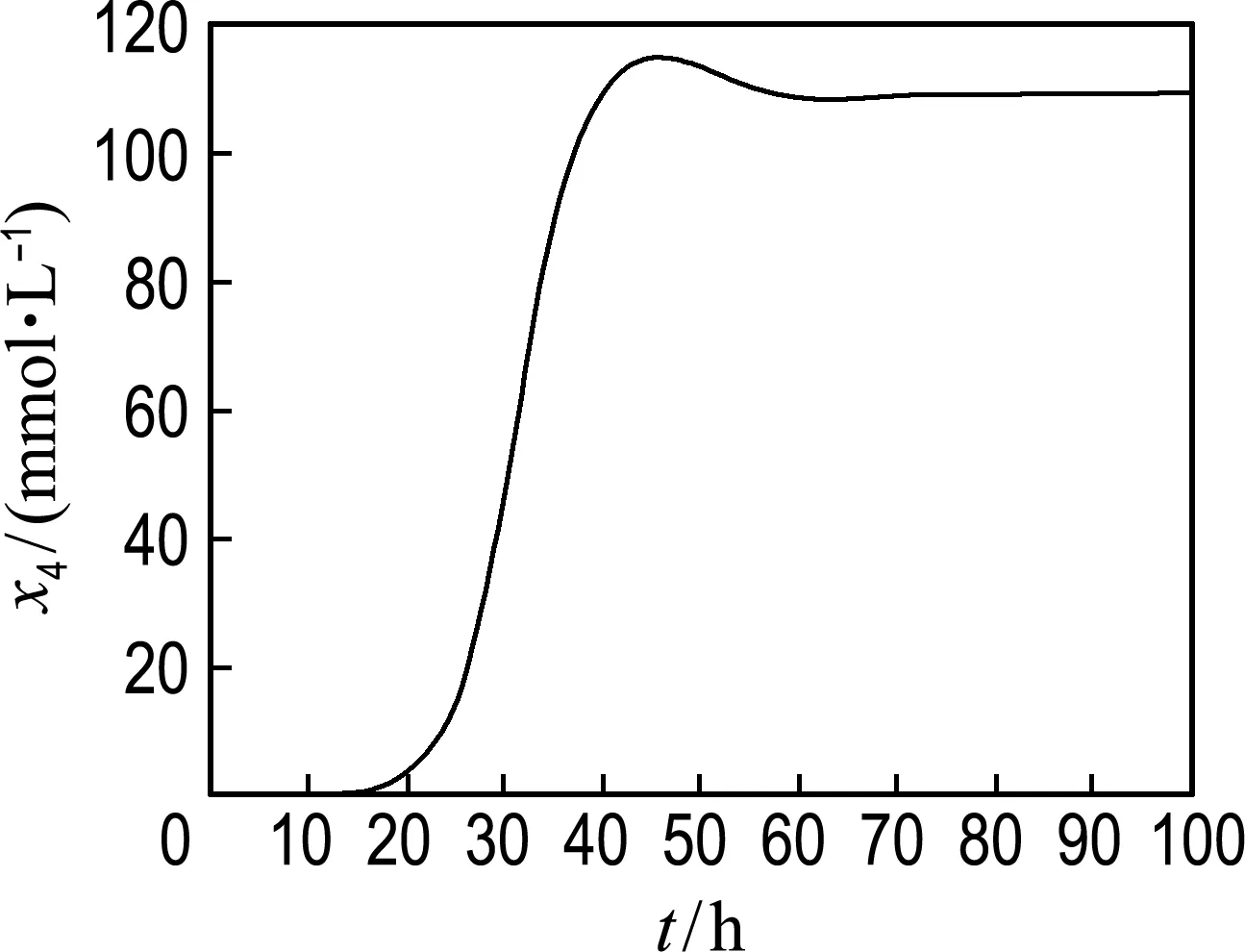
(d) 乙酸

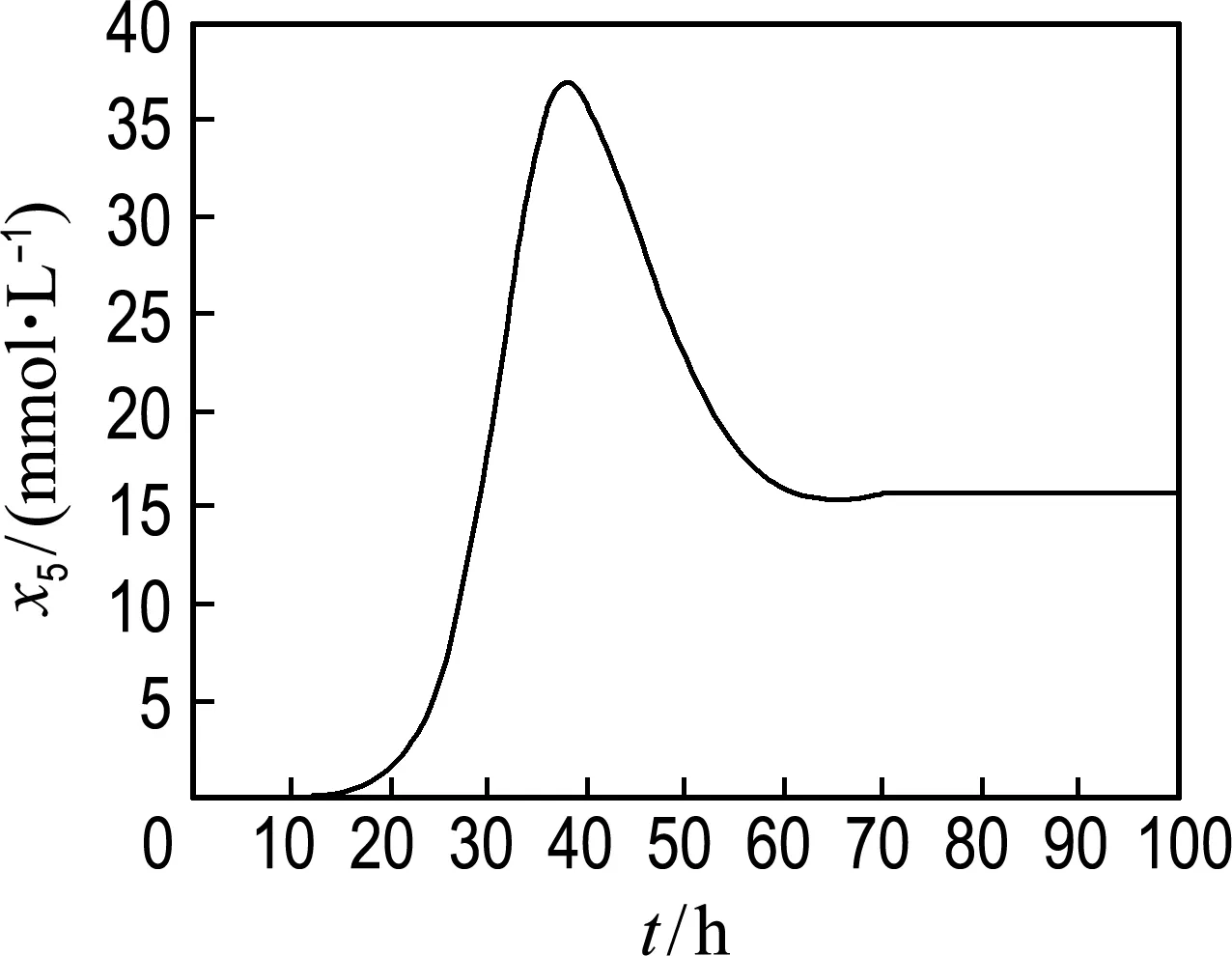
(e) 乙醇

圖3 生物質、甘油、1,3-丙二醇、乙酸、乙醇的濃度變化

Fig.3 The concentration change of biomass, glycerol, 1,3-PD, acetate and ethanol

5 結 語

本文提出了在微生物發酵生產1,3-丙二醇過程中的一種線性反饋控制策略．該策略可以很好地保證魯棒性，并通過精確罰方法給出了原問題的近似問題從而使用一種非線性優化算法二次序列規劃方法求得全局最優解，而且通過線性反饋策略優先實現了閉環控制．希望未來可以實現多階段的反饋控制，令反饋參數為與時間t相關的函數，從而更加精確地實現控制．

[1] LIU Chongyang, GONG Zhaohua, FENG Enmin,etal. Modelling and optimal control for nonlinear multistage dynamical system of microbial fed-batch culture [J].JournalofIndustrialandManagementOptimization, 2009,5(4):835-850.

[2] LIU Chongyang, GONG Zhaohua, TEO K L. Robust parameter estimation for nonlinear multistage time-delay systems with noisy measurement data [J].AppliedMathematicalModelling, 2018,53:353-368.

[3] YUAN Jinlong, ZHANG Yuduo, YE Jianxiong,etal. Robust parameter identification using parallel global optimization for a batch nonlinear enzyme-catalytic time-delayed process presenting metabolic discontinuities [J].AppliedMathematicalModelling, 2017,46:554-571.

[4] YUAN Jinlong, ZHANG Xu, ZHU Xi,etal. Modelling and pathway identification involving the transport mechanism of a complex metabolic system in batch culture [J].CommunicationsinNonlinearScienceandNumericalSimulation, 2014,19(6):2088-2103.

[5] 修志龍. 微生物發酵法生產1,3-丙二醇的研究進展[J]. 微生物學通報, 2000,27(4):300-302.

XIU Zhilong. Progress in the production of 1,3-PD by microorganism fermentation [J].MicrobiologyChina, 2000,27(4):300-302. (in Chinese)

[6] ZHANG Yuduo, FENG Enmin, XIU Zhilong. Robust analysis of hybrid dynamical systems for 1,3-propanediol transport mechanisms in microbial continuous fermentation [J].MathematicalandComputerModelling, 2011,54(11):3164-3171.

[7] GAO Kuikui, ZHANG Xu, FENG Enmin,etal. Sensitivity analysis and parameter identification of nonlinear hybrid systems for glycerol transport mechanisms in continuous culture [J].JournalofTheoreticalBiology, 2014,347:137-143.

[8] LV Jiajia, PANG Liping, FENG Enmin. Asymptotical stability of a nonlinear non-differentiable dynamic system in microbial continuous cultures [J].AdvancesinDifferenceEquations, 2017,2017:256. https://doi.org/10.1186/s13662-017-1288-X.

[9] GERDTS M, KUNKEL M. A nonsmooth Newton′s method for discretized optimal control problems with state and control constraints [J].JournalofIndustrialandManagementOptimization, 2008,4(2):247-270.

[10] WANG L Y, GUI W H, TEO K L,etal. Time delayed optimal control problems with multiple characteristic time points: computation and industrial applications [J].JournalofIndustrialandManagementOptimization, 2009,5(4):705-718.

[11] YU Changjun, LI Bin, LOXTON R,etal. Optimal discrete-valued control computation [J].JournalofGlobalOptimization, 2013,56:503-518.

[12] LI Bin, TEO K L, LIM C C,etal. An optimal PID controller design for nonlinear constrained optimal control problems [J].DiscreteandContinuousDynamicalSystems—SeriesB, 2011,16:1101-1117.

[13] LOXTON R, TEO K L, REHBOCK V,etal. Optimal control problems with a continuous inequality constraint on the state and the control [J].Automatica, 2009,45:2250-2257.

[14] LOXTON R, TEO K L, REHBOCK V. Robust suboptimal control of nonlinear systems [J].AppliedMathematicsandComputation, 2011,217:6566-6576.

[15] REHBOCK V, TEO K L, JENNINGS L S. A computational procedure for suboptimal robust controls [J].DynamicsandControl, 1992,2(4):331-348.

[16] FISHER M E, GRANTHAM W J, TEO K L. Neighbouring extremals for nonlinear systems with control constraints [J].DynamicsandControl, 1995,5:225-240.

[17] JIANG C, TEO K L, LOXTON R,etal. A neighboring extremal solution for an optimal switched impulsive control problem [J].JournalofIndustrialandManagementOptimization, 2012,8:591-609.

[18] ZHOU Jingyang, TEO K L, ZHOU Di,etal. Nonlinear optimal feedback control for lunar module soft landing [J].JournalofGlobalOptimization, 2012,52(2):211-227.

[19] LOXTON R, TEO K L, REHBOCK V. Optimal control problems with multiple characteristic time points in the objective and constraints [J].Automatica, 2008,44:2923-2929.

[20] PONTRYAGIN L S.TheMathematicalTheoryofOptimalProcesses[M]. New York: Gordan and Breach, 1986.

[21] BURDEN R L, FAIRES J D.NumericalAnalysis[M]. Boston: Brooks Cole, 2010.

[22] LIN Q, LOXTON R, TEO K L,etal. Optimal feedback control for dynamic systems with state constraints: An exact penalty approach [J].OptimizationLetters, 2014,8(4):1535-1551.

[23] GAO C X, WANG Z T, FENG E M,etal. Nonlinear dynamical systems of bio-dissimilation of glycerol to 1, 3-propanediol and their optimal controls [J].JournalofIndustrialandManagementOptimization, 2005,1(3):377-388.

[24] YU C, TEO K L, ZHANG L,etal. A new exact penalty function method for continuous inequality constrained optimization problems [J].JournalofIndustrialandManagementOptimization, 2010,6:895-910.

[25] 修志龍,曾安平,安利佳. 甘油生物歧化過程動力學數學模擬和多穩態研究[J]. 大連理工大學學報, 2004,40(4):428-433.

XIU Zhilong, ZENG Anping, AN Lijia. Mathematical modeling of kinetics and research on multiplicity of glycerol bioconversion to 1,3-propanediol [J].JournalofDalianUniversityofTechnology, 2000,40(4):428-433. (in Chinese)