基于TMD的鋼彈簧浮置板軌道結構改進研究

張龍慶

(中國鐵路設計集團有限公司，天津 300142)

城市軌道交通的快速發(fā)展有效地緩解了城市交通擁堵問題，但隨之而來的一系列環(huán)境問題引起了人們極大的關注[1]。軌道交通列車運行時由于輪軌相互作用引起的振動會對周圍環(huán)境造成一定的影響。一方面，其振動可能引起沿線建筑物的損傷開裂；另一方面，它可能會引起沿線一些博物館、醫(yī)院或者科研單位內(nèi)的精密儀器失靈；更甚者，長期的振動和噪聲可能會影響人類的正常生活和工作，甚至導致嚴重的精神和身體損傷[2]。

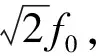
由此可見，“整體式”的減振方法和路線已經(jīng)走到了極限。動力吸振器[5-7](建筑土木工程領域稱為TMD)因其可以在預期頻段上實現(xiàn)降低主振動系的強迫振動響應，在交通運輸及土建結構等領域得到了廣泛應用。采用“分離式”被動減振技術的新型軌道結構形式將是軌道結構減振技術發(fā)展的一個重要方向[8-11]。

目前，國內(nèi)外已經(jīng)有很多關于動力吸振器的相關研究，但是有關動力吸振器在軌道工程中的應用則卻鮮見報道。通過對鋼彈簧浮置板軌道凸臺進行分離改進，并與凸臺下彈性元件連接組成TMD減振系統(tǒng)，進一步對軌道系統(tǒng)的低頻域制振效果進行分析，研究結果可為鋼彈簧浮置板軌道結構更低頻域制振提供一定的理論依據(jù)。

1 鋼彈簧浮置板軌道改進設計方法

鋼彈簧浮置板軌道改進方法如圖1所示。使用彈性元件將常規(guī)鋼彈簧浮置板軌道的凸臺與軌道板主板隔開，形成TMD減振系統(tǒng)，合理匹配凸臺與彈性元件的參數(shù)，將軌道板主板的低頻域共振能量吸收并加以增幅，通過TMD減振系統(tǒng)中的阻尼元件消耗，進而實現(xiàn)鋼彈簧浮置板軌道系統(tǒng)的低頻域制振性能。改進后的鋼彈簧浮置板軌道如圖2所示。

圖1 鋼彈簧浮置板軌道改進原理

圖2 改進后的鋼彈簧浮置板軌道

鋼彈簧浮置板軌道為一個連續(xù)系統(tǒng)，基于TMD定點理論以及多自由度系統(tǒng)等價質(zhì)量識別法，其各階模態(tài)TMD(動力吸振器)的設計方法在文獻[9]中已給出。

由文獻[9]可知，無凸臺鋼彈簧浮置板系統(tǒng)第i階模態(tài)的等價質(zhì)量為

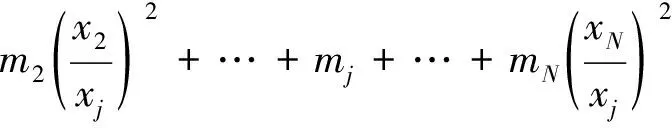
(1)

式中，Mi為從第j個自由度觀察到的第i階模態(tài)的具有物理含義的等價質(zhì)量；Ttotal為浮置板軌道系統(tǒng)全體的動能；(x1，x2，…，xj，…，xN)為浮置板軌道系統(tǒng)第i階模態(tài)的固有向量；(m1，m2，…，mj，…，mN)為離散的單自由度質(zhì)量；ωi為第i階固有圓頻率。

系統(tǒng)在第i階模態(tài)的等價剛度

(2)

這樣，浮置板第i階模態(tài)TMD的最優(yōu)參數(shù)如下。

(1)TMD質(zhì)量(本文為凸臺質(zhì)量)

mi=μiMi

(3)

(2)彈性元件最優(yōu)彈簧剛度

(4)

(3)彈性元件最優(yōu)阻尼系數(shù)

(5)

式(3)～式(5)中，μi為質(zhì)量比；mi為浮置板第i階模態(tài)TMD質(zhì)量；Mi為浮置板第i階模態(tài)等價質(zhì)量；Ki為浮置板第i階模態(tài)等價剛度；ki為浮置板第i階模態(tài)TMD最優(yōu)剛度；ci為浮置板第i階模態(tài)TMD最優(yōu)阻尼；Zi為浮置板第i階模態(tài)等價阻尼；ζi為浮置板第i階模態(tài)等價阻尼比[9]。

由以上公式可知，已知凸臺的質(zhì)量，然后通過有限元方法計算得到無凸臺鋼彈簧浮置板軌道系統(tǒng)的等價質(zhì)量Mi，便可通過公式(3)得到質(zhì)量比μi，進而通過文獻[9]的計算方法可得到凸臺下彈性元件的最優(yōu)剛度以及最優(yōu)阻尼系數(shù)。

值得注意的是，浮置板動力吸振器最優(yōu)位置應選擇該階模態(tài)的波腹位置，同時為了減少模態(tài)間的相互耦合作用影響，該位置應盡可能選在其他階模態(tài)的節(jié)點位置。

2 鋼彈簧浮置板軌道凸臺下彈性元件最優(yōu)參數(shù)設計

為方便分析，這里利用有限元軟件ANSYS建立了短型鋼彈簧浮置板軌道有限元模型，如圖3所示。參考某地鐵線路浮置板軌道實際設計參數(shù)，選取軌道板的長、寬、厚分別為3.6，2.8，0.32 m。模型采用Beam188單元模擬鋼軌，Solid45單元模擬鋼彈簧浮置板道床，Combine14單元模擬扣件系統(tǒng)和鋼彈簧的剛度、阻尼。扣件系統(tǒng)和鋼彈簧垂向靜剛度分別取30 kN/mm和6.6 kN/mm，鋼彈簧支座垂向阻尼比取5%。另外，將鋼軌視為離散支承的無限長歐拉梁，在其兩端施加簡支約束；軌道板縱向兩端面施加對稱約束來模擬浮置板之間的剪力鉸；并對鋼彈簧底部的所有節(jié)點施加固定約束。

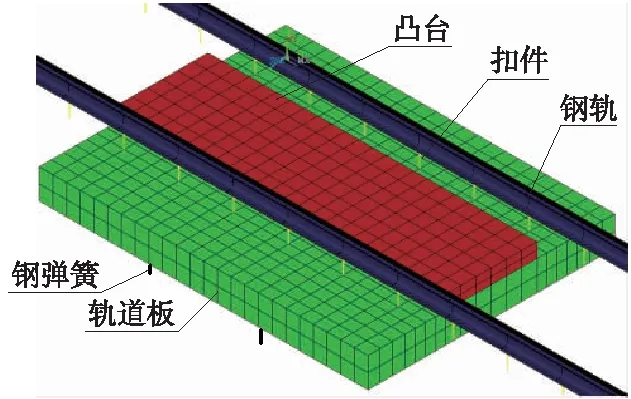
圖3 鋼彈簧浮置板軌道有限元模型

由于本文旨在增強鋼彈簧浮置板軌道低頻域制振效果，故這里考慮將凸臺通過彈性元件改造為浮置板軌道一階模態(tài)TMD。利用以上有限元模型計算獲得無凸臺鋼彈簧浮置板軌道第一階模態(tài)如圖4所示，圖中下部輪廓線為浮置板軌道未變形時的位置。從圖4可以看出，該鋼彈簧浮置板軌道一階模態(tài)為平動模態(tài)，其第一階固有頻率為13.71 Hz。

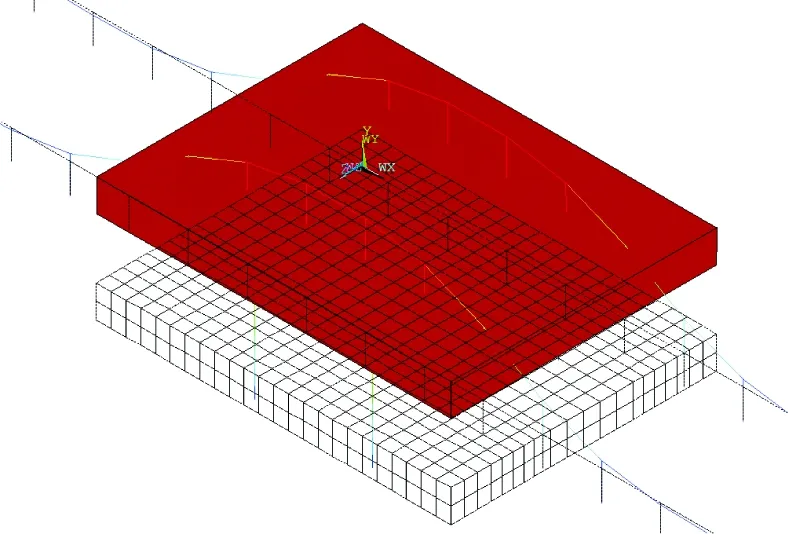
圖4 無凸臺浮置板軌道一階模態(tài)振型

基于多自由度系統(tǒng)等價質(zhì)量識別法，通過ANSYS計算得到無凸臺鋼彈簧浮置板軌道一階模態(tài)總能量Ttotal和最大模態(tài)位移x1，并將其與一階固有頻率ω1一同代入到公式(1)中，得到無凸臺鋼彈簧浮置板軌道系統(tǒng)等價質(zhì)量M1，再利用凸臺質(zhì)量m通過公式(2)得到質(zhì)量比μ，進而結合公式(3)～(5)并基于TMD最優(yōu)同調(diào)原則得到彈性元件最優(yōu)剛度和最優(yōu)阻尼系數(shù)如表1所示。

表1 鋼彈簧浮置板凸臺及其下部彈性元件最優(yōu)參數(shù)

得到以上參數(shù)后，利用有限元軟件ANSYS建立有限元模型，對比分析了單位簡諧荷載作用下，常規(guī)鋼彈簧浮置板軌道與改進后的鋼彈簧浮置板軌道板中幅頻響應曲線如圖5所示。

圖5 鋼彈簧浮置板軌道改進前后板中幅頻響應

從圖5可以看出，單位簡諧荷載作用下，常規(guī)鋼彈簧浮置板軌道在一階固有頻率13.7 Hz附近頻段產(chǎn)生明顯的共振現(xiàn)象，在幅頻響應曲線上出現(xiàn)明顯的共振峰值；改進后的鋼彈簧浮置板軌道幅頻響應曲線在常規(guī)浮置板軌道一階固有頻率附近頻段的共振峰值明顯得到抑制；與此同時，改進后的鋼彈簧浮置板軌道在常規(guī)浮置板軌道一階固有頻率左右各出現(xiàn)一個較小的峰值，且兩峰值等高，表明凸臺與下部彈性聯(lián)結元件組成的TMD減振系統(tǒng)達到了最優(yōu)同調(diào)條件[11]，可將該減振系統(tǒng)的共振抑制效果提升到最優(yōu)。

3 鋼彈簧浮置板軌道改進前后低頻域吸振特性分析

基于車輛-軌道耦合動力學理論[12-16]，通過自編程序?qū)崿F(xiàn)車輛運行行為模擬，計算得到輪軌相互作用力，并將其施加到改進前后的鋼彈簧浮置板軌道有限元模型(圖6)上進行動力學分析。車輛采用地鐵標準B2型車，運行時速為80 km，主要性能參數(shù)參見文獻[8]。在沒有實測軌道不平順條件下，根據(jù)城市軌道交通軌道特點，軌道不平順采用了波長范圍為1～30 m美國五級軌道譜。

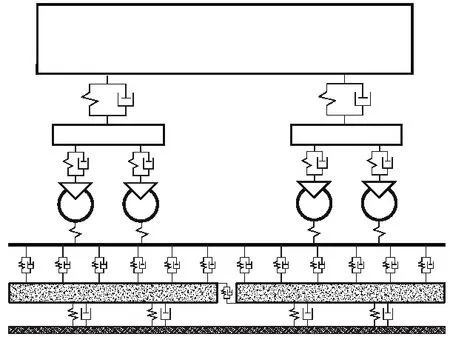
圖6 地鐵車輛-鋼彈簧浮置板軌道耦合動力學模型

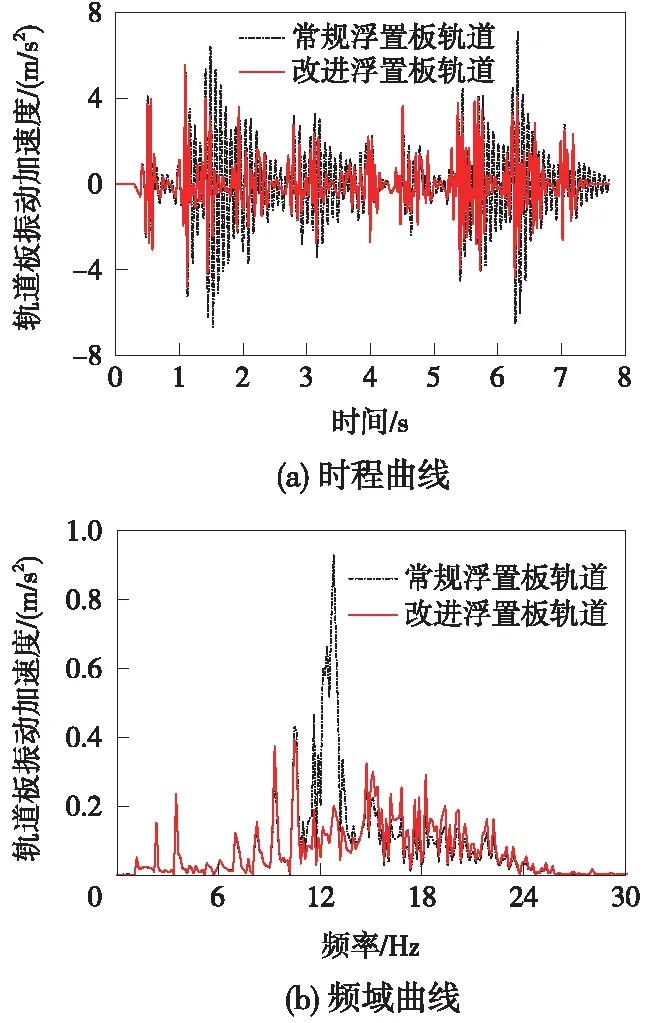
圖7 浮置板板中振動加速度

基于以上車輛-軌道耦合動力學模型，分析了列車荷載作用下鋼彈簧浮置板軌道改進前后的吸振特性。圖7為鋼彈簧浮置板軌道改進前后的加速度時域響應和頻域響應對比圖。由圖7(a)可知，浮置板軌道主板的加速度幅值由改進前的7.12 m/s2降至改進后的5.56 m/s2，降幅達21.9%，且改進后的浮置板主板的加速度衰減速度明顯高于常規(guī)浮置板主板的加速度衰減速度。由圖7(b)可知，列車荷載作用下，常規(guī)浮置板軌道主板振動加速度在其一階固有頻率13.7 Hz附近出現(xiàn)明顯的共振峰值，通過凸臺改進后的浮置板主要的振動加速度峰值在該共振頻段得到明顯抑制，表明改進后的鋼彈簧浮置板軌道能夠有效抑制軌道系統(tǒng)低頻域共振的發(fā)生。

輪軌相互作用力通過軌枕結構、隧道結構等傳遞到周圍土體，再通過周圍土體向附近的民宅、建筑物傳播。而鋼彈簧支座反力能明確反映出軌道結構傳遞到下部基礎的列車作用荷載。圖8給出了鋼彈簧支座反力的時域和頻域曲線。從圖8(a)可以看出，改進后的浮置板軌道較常規(guī)浮置板軌道鋼彈簧支座反力峰值稍有降低，但不明顯。從圖8(b)可以看出，地鐵B2型車經(jīng)過常規(guī)鋼彈簧浮置板軌道時會引起軌道系統(tǒng)一階固有頻率附近頻段的鋼彈簧支座反力共振放大產(chǎn)生明顯的峰值，改進后的鋼彈簧浮置板軌道鋼彈簧支座反力在該頻段得到明顯抑制，表明改進后的鋼彈簧浮置板軌道能夠有效抑制軌道系統(tǒng)低頻域共振頻段鋼彈簧支座反力向下部基礎的傳遞，從而降低了輪軌相互作用引起的低頻共振振動向周圍建筑物的傳遞，有效緩解了低頻振動對周邊環(huán)境的損害。

圖8 浮置板下鋼彈簧支座反力

圖9為鋼彈簧浮置板軌道改進前后浮置板主板振動加速度級對比圖。從圖9可以看出，在軌道系統(tǒng)一階固有頻率13 Hz附近頻段，常規(guī)浮置板軌道振動加速度級出現(xiàn)明顯的共振峰值，相比于常規(guī)浮置板軌道，改進后的鋼彈簧浮置板軌道振動加速度級顯著降低。表明改進后的浮置板軌道較常規(guī)浮置板軌道有良好的低頻域吸振效果。

圖9 浮置板板中加速度1/3倍頻程

鋼彈簧浮置板軌道系統(tǒng)采取減隔振措施后，其吸振效果可通過插入損失明顯地表達出來。本文中鋼彈簧浮置板軌道改進前后的插入損失可通過以上振動加速度振級差值表示。當插入損失大于零時，表明改進后的鋼彈簧浮置板軌道相較與常規(guī)鋼彈簧浮置板軌道有吸振效果；當插入損失小于零時，說明改進后的鋼彈簧浮置板軌道相比于常規(guī)鋼彈簧浮置板軌道沒有吸振效果，反而在一定程度上放大了浮置板軌道系統(tǒng)的振動。

圖10給出了常規(guī)鋼彈簧浮置板軌道較改進后的鋼彈簧浮置板軌道插入損失。從圖10可知，改進后的鋼彈簧浮置板軌道能夠?qū)ΤＲ?guī)鋼彈簧浮置板軌道低頻域共振振動起到充分的抑制作用，相較于常規(guī)鋼彈簧浮置板軌道，改進后的鋼彈簧浮置板軌道最大吸振效果達到11.42 dB。

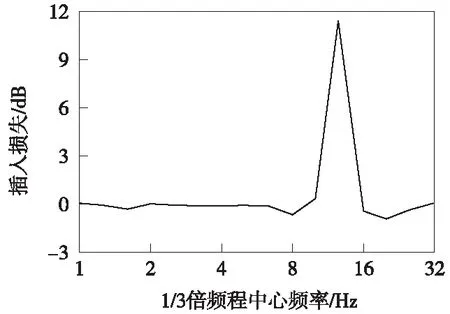
圖10 鋼彈簧浮置板軌道改進前后軌道板插入損失

4 結論

(1)基于定點理論以及多自由度系統(tǒng)等價質(zhì)量識別法，能夠準確地確定改進后鋼彈簧浮置板軌道凸臺下的剛度阻尼參數(shù)，并組成有效的減振系統(tǒng)。

(2)通過TMD減振技術改進得到的鋼彈簧浮置板軌道能夠有效抑制常規(guī)浮置板軌道低頻域共振放大現(xiàn)象，并能有效地降低該頻段的低頻振動向周圍建筑物的傳遞，緩解了該頻段低頻振動對周圍基礎設施的損害。

(3)改進后的鋼彈簧浮置板軌道能夠?qū)ΤＲ?guī)鋼彈簧浮置板軌道低頻域共振振動起到充分的抑制作用，相較于常規(guī)鋼彈簧浮置板軌道，改進后的鋼彈簧浮置板軌道最大吸振效果可達11.42dB。

[1] 夏禾，曹艷梅.軌道交通引起的環(huán)境振動問題[J].鐵道科學與工程學報，2004(1)：44-51.

[2] 金浩，劉維寧，周順華.板下減振墊對橡膠浮置板軌道減振性能的影響[J].鐵道科學與工程學報，2016，13(2)：245-249.

[3] Lombaert G， Degrande G， Vanhauwere B， et al. The Control Of Ground-Borne Vibration From Railway Traffic By Means Of Continuous Floating Slabs[J]. Journal of Sound and Vibration， 2006，297(3-5)：946-961.

[4] 丁德云.地鐵列車振動環(huán)境響應低頻特征的分析與研究[D].北京：北京交通大學，2010.

[5] Anh N D， Nguyen N X. Design of non-traditional dynamic vibration absorber for damped linear structures[J]. Proceedings of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering Science， 2014，228(1)：45-55.

[6] Anh N D， Nguyen N X， Hoa L T. Design of three-element dynamic vibration absorber for damped linear structures[J]. Journal of Sound and Vibration， 2013，332(19)：4482-4495.

[7] Noori B， Farshidianfar A. Optimum design of dynamic vibration absorbers for a beam， based on H∞ and H2Optimization[J]. Archive of Applied Mechanics， 2013，83(12)：1773-1787.

[8] 張龍慶.基于動力吸振器的浮置板軌道低頻振動控制研究[D].成都：西南交通大學，2016.

[9] 張龍慶，朱勝陽，蔡成標，等.動力吸振器在浮置板軌道低頻振動控制中的應用[J].工程力學，2016，33(9)：212-219.

[10] Thmpson D J， Jones C J C，Waters T P， et al. A turned damping device for reducing noise from railway track[J]. Applied Acoustics， 2007，68(1)：43-57.

[11] 背戶一登.動力吸振器及其應用[M].任明章，譯.北京：機械工業(yè)出版社，2013.

[12] 蔡成標.高速鐵路列車-線路-橋梁耦合振動理論及應用研究[D].成都：西南交通大學，2004.

[13] 翟婉明.車輛-軌道耦合動力學(上)[M].4版.北京：科學出版社，2015.

[14] 翟婉明.車輛-軌道耦合動力學(下)[M].4版.北京：科學出版社，2015.

[15] Zhu S， Yang J， Yan H， et al. Low-frequency vibration control of floating slab tracks using dynamic vibration absorbers[J]. Vehicle System Dynamics， 2015，53(9)：1296-1314.

[16] 肖威，郭宇，高建敏，等.高速鐵路路基不均勻沉降對CRTSⅢ板式軌道受力變形的影響[J].鐵道科學與工程學報，2015，12(4)：724-730.