重載鐵路部分斜拉橋結構參數分析

李桂林

(中鐵第四勘察設計院集團有限公司,武漢 430063)

1 概述

各種橋型對于跨度均有不同的適用范圍，預應力混凝土連續梁存在自重較大等特點，應用于鐵路橋梁時其主跨跨度一般在128 m范圍內。部分斜拉橋作為一種連續梁拉索加勁結構，可擴展其跨度，應用跨度范圍為140～280 m。與連續梁相比，部分斜拉橋具有提供較大的跨越能力、有效控制后期變形等優點；與常規斜拉橋相比其主要有節省工程量、結構剛度大、施工周期短等優勢，因此在高速鐵路、城際鐵路及公路工程中得到廣泛應用。

重載鐵路作為純貨運鐵路形式，與客運專線、高速鐵路、客貨共線鐵路相比，存在設計荷載大、軸重重、列車荷載頻繁等特點[1-2]。蒙華重載鐵路跨越漢江時，考慮到與下游5×120 m公路連續梁橋對孔及經濟性等邊界條件，根據多方案比選，采用主跨248 m部分斜拉橋方案[3]。由于活載所占比重極大，直接采用目前典型的部分斜拉橋形式及結構設計參數范圍，結構難以承受。為解決部分斜拉橋應用于重載鐵路橋梁受力問題，對該橋各參數進行比較分析，確定部分斜拉橋應用于該橋位時的合理結構參數，并首次成功將部分斜拉橋應用于重載鐵路[4-6]。部分斜拉橋效果圖見圖1。

圖1 部分斜拉橋效果圖

2 約束體系分析

本橋主跨跨度達248 m，又為重載鐵路，僅列車荷載單項引起主墩支反力達49 280 kN，如采用塔梁固結、墩梁分離體系[7-10]，需特殊設計大噸位支座。理論上來說，宜優先考慮塔墩梁固結體系，避免設置大噸位支座。

該橋小里程側主墩墩高18.2 m，大里程側主墩墩高18.7 m(均為梁底至地面線之間的距離)，約為跨度的1/13.3。當采用塔墩梁固結體系時，由于主墩高跨比較小，若采用較剛的橋墩形式，溫度產生自應力較大，墩底及主梁均承受較大拉應力作用，結構難以承受。此時若采用雙肢薄壁墩等較柔的結構形式，則主墩截面面積及慣性矩均偏小，最大壓應力已超目前最大混凝土強度等級壓應力限值，結構受力性能差，且存在防撞能力差、侵占通航凈空等不利因素。

從主梁受力分析，在恒載及列車荷載作用下，雙肢薄壁體系能有效改善支點截面負彎矩和跨中截面正彎矩作用。但采用塔墩梁固結體系與塔梁固結、墩梁分離體系比較，溫度引起主梁支點截面彎矩增大54倍，跨中截面彎矩增大34倍。同時，在預應力鋼束布置一致的情況下，塔梁固結、墩梁分離體系時預應力效應能更有效的發揮，總體應力水平塔梁固結、墩梁分離體系偏優。

從活載位移結果比較分析，采用塔梁固結、墩梁分離體系時剛度為1/1 042，塔墩梁固結體系時剛度為1/1 941，可以看出塔墩梁固結體系能有效提高結構整體剛度，從剛度這方面分析，塔墩梁固結體系具有較明顯的優勢，但由于本橋為重載鐵路，對結構剛度及行車舒適性等要求較低，結構剛度為非控制性因素。

綜合分析，受橋位處墩高限制，采用塔墩梁固結體系時結構難以實現，比選后采用塔梁固結、墩梁分離體系，并于主墩設置190 000 kN球形支座，為目前國內第二大噸位，支座采用高性能材料及分部密封方案，保證耐久性、穩定性和長久使用壽命。

3 主梁梁高影響分析

為研究主梁高度對主梁受力性能的影響程度，研究主梁支點梁高為13、13.5 m和14 m，跨中梁高為6 m和6.5 m時梁高組合，分析主梁內力及應力情況。表1列出不同梁高時各控制點最不利荷載組合應力。

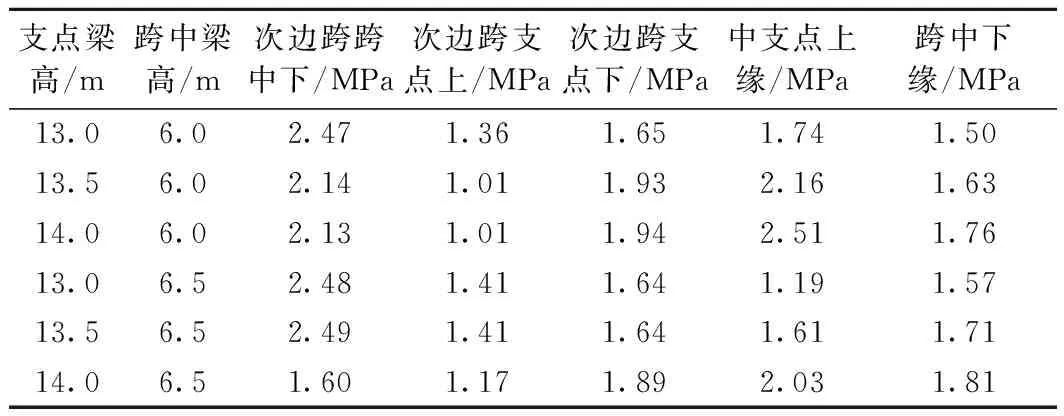
表1 主梁控制點應力對比

注：應力值以壓為正。

增加支點梁高及跨中梁高，跨中下緣應力儲備增幅在0.3 MPa以下；對中支點截面，最佳方案為14 m-6 m組合，中支點上緣壓應力增加0.77 MPa；對于邊跨來說，13.5 m-6.5 m組合最優，但與13 m-6 m組合僅差別0.05 MPa。總體來看，無論是增加支點梁高，還是跨中梁高，對截面應力改善影響程度均較小，而13 m-6 m組合時，主梁應力已呈現較好的應力狀態，表明該梁高取值合適。中支點梁高13 m，跨中梁高6 m情況下，邊跨上緣最大壓應力為15 MPa，中跨上緣最大壓應力為17.4 MPa，且跨中下緣壓應力儲備仍有1.5 MPa富余。中支點梁高采用13 m時，嘗試減少跨中梁高至5.5 m，跨中混凝土上緣壓應力高達19.7 MPa，次邊跨支點上、下緣最大壓應力均達到19.1 MPa，此時最小應力僅為0.12 MPa。表明該梁高偏小，不宜再減小梁高。

通過對梁高比較可知：在一定范圍內無論是增加跨中梁高還是支點梁高，主梁應力改善影響程度均較小，同時主墩噸位將會超190 000 kN。當降低梁高時，主梁上緣壓應力高達19.7 MPa，梁高不宜再降低。因此中支點—跨中梁高采用13 m-6 m組合較為合適。

4 預應力鋼束布置對結構內力影響分析

本橋主梁為5跨連續梁形式，采用先合龍邊跨后合龍中跨方案，需進行三次體系轉換，預應力布置復雜。由于斜拉索對邊支點及邊跨跨中影響甚微，因此需要研究該區域頂底板鋼束布置及張拉順序形式對結構內力影響，同時分析中跨底板短束和長束對結構內力影響，確定最合理的預應力鋼束布置方式。典型鋼束布置示意如圖2所示。

看完這封信，我的頭一個反應是，糟了，白麗筠一定是尋了短見。我發了瘋一般沖出家門，本能地朝白麗筠的住所奔去。只見她家的門大敞著，有工人搬著笨重的大件家具進進出出。我努力鎮靜自己，裝出一副路人的好奇，朝門里探頭張望，門里已經完全是另一個世界，哪里還有白麗筠住過的痕跡。

圖2 典型鋼束布置示意

對圖2中6種對邊跨影響較大的預應力布置形式及相應工況進行分析(均為2束19-φj15.2 mm鋼束效應)，對結構影響主要呈現以下特性。

(1)邊跨頂板短束T3在懸臂張拉階段及在邊跨合龍后張拉這兩種工況下，軸力接近，均為6 500 kN左右。懸臂張拉工況在輔助墩產生彎矩為16 862 kN·m，截面上緣產生0.7 MPa壓應力，截面下緣產生0.2 MPa拉應力；邊跨合龍后張拉時彎矩10 467 kN·m，截面上緣產生0.6 MPa壓應力，截面下緣產生0.1 MPa壓應力。輔助墩位置上下緣均為控制區域，在上緣應力改善需求明顯的情況下，可增加懸臂張拉短索根數，若上下緣應力均較為控制，宜增加邊跨合龍后短索根數。

(2)邊跨頂板長索T10(未越過邊跨合龍段)，該類型鋼束主要為改善輔助墩頂受力。懸臂階段張拉時，于輔助墩頂區域產生正應力，但邊跨塔端無索區次內力作用明顯。邊跨合龍后張拉和中跨合龍后張拉彎矩圖接近，于輔助墩頂區域為負效應。從3種張拉階段產生的彎矩(圖3)來看，以懸臂階段張拉為優，但該類型鋼束次內力負效應較明顯，在滿足施工階段節段混凝土張拉鋼束要求的前提下，應盡量減少該類型鋼束布置。

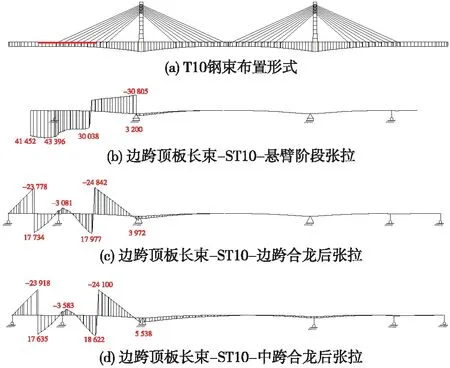
圖3 邊跨頂板長索T10彎矩(單位：kN·m)

(3)邊跨頂板長束T11(越過邊跨合龍段)，在邊跨合龍后及中跨合龍后張拉，彎矩圖均接近，主要在邊跨產生正彎矩，中跨產生負彎矩，且該鋼束僅影響邊跨及次邊跨受力，對中跨彎矩影響甚微。

(4)邊跨底板短束B1，于邊跨合龍后張拉及中跨合龍后張拉各截面彎矩值接近，彎矩主要集中在鋼束布置區域，且分布較均勻，近似呈矩形分布，約為14 800 kN·m，該類型鋼束次內力效應較小。

(5)B5和B6彎矩圖較為接近，主要在邊跨產生負彎矩效應，呈近似梯形分布，于次邊跨2/3范圍內產生近似三角形分布正彎矩。B6鋼束布置越過輔助墩，梯形分布負彎矩亦越過輔助墩，能改善輔助墩底應力水平。見圖4。

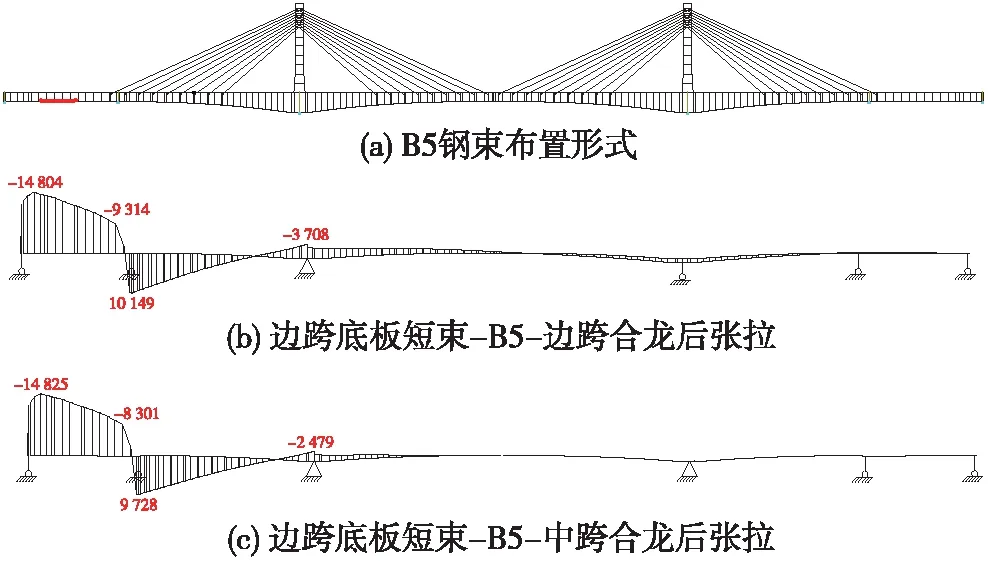
圖4 邊跨底板長索B5彎矩(單位：kN·m)

5 橋塔剛度影響分析

橋塔采用雙柱式，橋面以上塔高57.0 m，順橋向塔底寬7.2 m，塔頂寬5.0 m；橫橋向寬度2.8 m。為研究橋塔剛度對結構受力的影響，分析了以0.1、0.5、1、5、10倍橋塔剛度時結構特性。見表2。

表2 橋塔剛度對應工況控制截面彎矩對比

主力工況下，中支點截面最大彎矩隨剛度增加而減少[11-15]，跨中截面彎矩隨剛度增加先減少后增大，1倍橋塔剛度時最小。主力+附加力工況下，中支點截面彎矩隨橋塔剛度增加而減小，10倍橋塔剛度時對應彎矩較之0.1倍橋塔剛度時彎矩減小12%，主跨跨中截面10倍橋塔剛度時對應彎矩較之0.1倍橋塔剛度時減小7%。

從表3可以看出，橋塔剛度增加10倍的情況下，結構整體剛度僅增加1.012%。

表3 橋塔剛度對應結構整體剛度值

從以上分析可知，重載鐵路部分斜拉橋橋塔剛度對結構整體受力及結構剛度影響均較小，可在滿足索鞍布置等構造及橋塔自身受力要求的前提下[16-18]，盡可能減少橋塔尺寸，降低橋塔混凝土用量。

6 橋塔高度影響分析

對35 m/40 m/45 m/50 m/57 m塔高時結構分析，控制截面彎矩如表4所示。

主力工況下，主梁中支點彎矩隨橋塔高度增大而減小，57 m塔高時對應彎矩為35 m塔高時對應彎矩的63%，主梁跨中彎矩隨橋塔高度增加而減小，且降幅明顯，57 m塔高時對應彎矩僅為35 m塔高時對應彎矩的51.6%。主力加附加力工況下，亦呈現出與主力工況下相似結論，57 m塔高時對應中支點彎矩為37 m塔高時的64.7%，57 m塔高時跨中截面彎矩為35 m塔高時的58.1%，降幅均非常明顯。

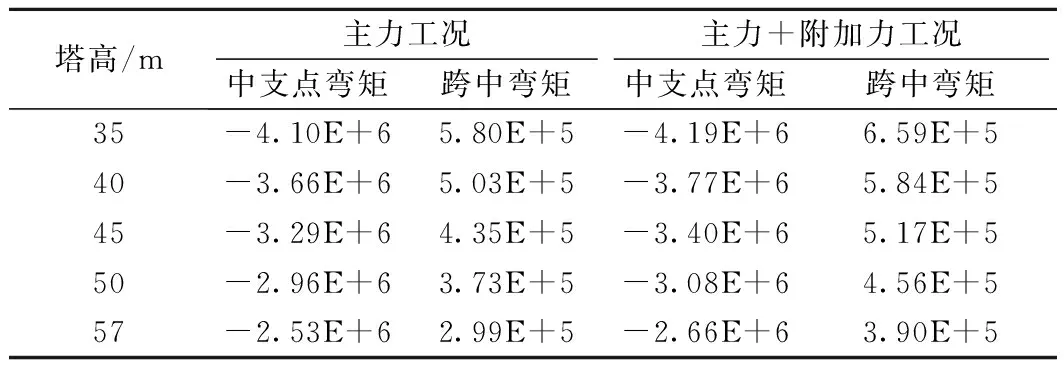
表4 主力工況下控制截面彎矩對比 kN·m

由表5可以看出，橋塔高度對主梁剛度有一定程度影響，當橋塔高度降低38.6%，主梁剛度降低17.1%。

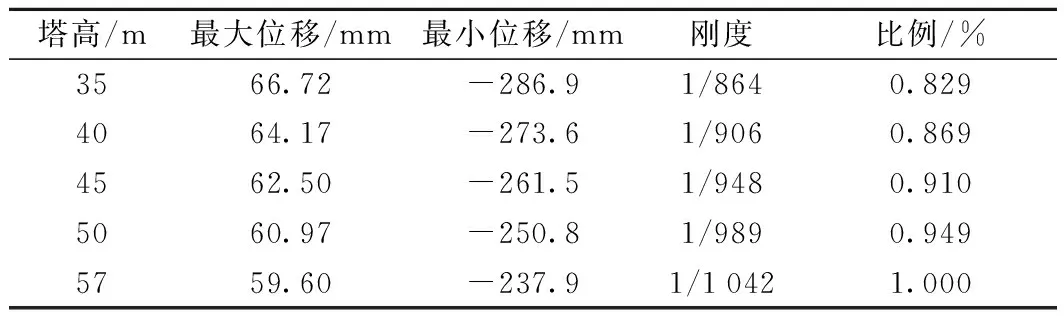
表5 塔高對應結構剛度值

綜上所述，塔高是該重載鐵路部分斜拉橋的一個重要參數，其對主梁主跨支點截面及跨中彎矩均有很大影響，并在一定程度上影響著主梁剛度。

7 索塔梁剛度匹配分析

對于預應力混凝土連續梁，在跨度確定的情況下，梁高為橋梁結構剛度的控制因素。對于預應力混凝土部分斜拉橋，除梁高外，橋塔和斜拉索均對結構剛度存在較大影響。根據梁高對比分析，本橋主梁在截面應力優化且強度滿足規范要求的條件下，采用支點-跨中梁高13 m-6 m組合，不考慮設置橋塔及斜拉索時，主梁在靜活載作用下最大位移為355 mm，主梁剛度為1/698。考慮橋塔及斜拉索之后，結構剛度為1/1042，可知該橋主梁對整體剛度的貢獻值為67%，橋塔及斜拉索對整體剛度貢獻值為33%。橋塔和斜拉索為相關構件，橋塔自身剛度變化對主梁剛度影響很小，而當橋塔高度降低38.6%，主梁剛度降低17.1%，剛度為1/864，在此基礎上，斜拉索截面剛度降低38.6%，則主梁剛度變為1/827，結構剛度僅下降4.3%。從改變橋塔自身剛度、橋塔高度和斜拉索截面剛度相同比例的結果來看，改變橋塔高度對結構剛度的影響程度更大。

8 結論

本結構為混凝土主梁采用斜拉索加勁的部分斜拉橋形式，在重載鐵路工程項目中屬首次采用，填補了重載鐵路橋型空白。本橋通車運營時間約為2018年12月。通過對該橋的各設計參數的比較分析，主要得到以下結論。

(1)對比分析塔墩梁固結體系和塔梁固結、墩梁分離體系，從結構受力合理性等方面考慮，本橋采用墩梁分離體系要優于雙肢薄壁墩體系。

(2)以中支點-跨中梁高采用13 m-6 m作為基本組合梁高，在一定范圍內無論是增加跨中梁高還是支點梁高，主梁應力改善影響程度均較小，跨中梁高減少至5.5 m時，主梁上緣壓應力高達19.7 MPa，此時上緣最小壓應力僅為0.12 MPa，梁高不宜再降低。中支點-跨中梁高采用13 m-6 m組合是合理選擇。

(3)短預應力鋼束引起彎矩主要分布于預應力鋼束布置區域，且近似呈矩形分布，預應力次內力效應較小；邊跨頂板長束效應較差，應適當減少該類型鋼束布置，邊跨底板長束彎矩在邊跨區域負彎矩呈近似梯形分布，于次邊跨正彎矩呈近似三角形分布，次內力效應明顯。

(4)重載鐵路部分斜拉橋橋塔剛度對結構整體受力及結構剛度影響均較小，可在滿足索鞍布置等構造及橋塔自身受力要求的前提下，盡可能減少橋塔尺寸，降低橋塔混凝土用量。

(5)結合重載鐵路特點，通過對橋塔高跨比研究，確定橋塔高采用57 m，高跨比為1/4.35，普通鐵路部分斜拉橋橋塔高跨比一般在1/7.0～1/7.5，較普通鐵路部分斜拉橋高跨比大。高跨比增大，能有效改善重載鐵路部分斜拉橋主梁受力，保證在重載鐵路荷載作用下，結構具有足夠的強度、剛度等性能。

(6)該重載鐵路部分斜拉橋結構剛度主要由主梁提供，約占67%，主塔及拉索對整體剛度貢獻值為33%，主塔自身剛度對結構整體剛度影響甚微，橋塔高度對結構剛度影響較明顯。

[1] 金福海，文望青，許三平.蒙西至華中地區鐵路煤運通道設計活載選用初探[J].鐵道標準設計，2013，57(3)：48-52.

[2] 李桂林.超大跨度鐵路橋梁列車加載長度研究[J].鐵道標準設計，2015，59(3):64-68.

[3] 嚴定國.蒙西至華中地區鐵路煤運通道漢江特大橋方案設計[J].鐵道標準設計，2016，60(7)：99-103.

[4] 國家鐵路局.TB/T 3466—2016 鐵路列車荷載圖示[S].北京：中國鐵道出版社，2016.

[5] 國家鐵路局.TB 10625—2017/J2289—2017 重載鐵路設計規范[S].北京：中國鐵道出版社，2017.

[6] 國家鐵路局.TB 10092—2017/J462—2017 鐵路橋涵混凝土結構設計規范[S].北京：中國鐵道出版社，2017.

[7] 張雷.京滬高速鐵路津滬聯絡線矮塔斜拉橋設計[J].橋梁建設，2012，42(4)：69-74.

[8] 王富君.跨既有鐵路矮塔斜拉橋設計與轉體施工[J].鐵道標準設計，2011(3)：58-61.

[9] 劉士林.斜拉橋設計[M].北京：人民交通出版社，2006.

[10] 嚴國敏.現代斜拉橋[M].成都：西南交通大學出版社，1999.

[11] 藺鵬臻.部分斜拉橋的力學性能及其界定[J].鐵道學報，2007，29(2)：136-140.

[12] 燕明.部分斜拉橋的概念與結構設計[J].交通科技與經濟，2006(3)：11-13.

[13] 康煒.小西湖黃河大橋部分斜拉橋結構分析[J].鐵道標準設計，2004(11)：88-90.

[14] 鄭一峰，黃僑，張連振.部分斜拉橋結構對比分析[J].公路，2005(11)：15-21.

[15] 張海，吳大宏.津保鐵路矮塔斜拉橋設計關鍵技術研究[J].鐵道標準設計，2013，57(11)：55-58.

[16] 陳虎成，石雪飛.部分斜拉橋結構性能研究[J].結構工程師，2004(3)：27-31.

[17] 陳從春，周海智，肖汝誠.矮塔斜拉橋研究的新進展[J].世界橋梁，2006(1)：70-73.

[18] 陳軍剛，陳孔令，張焱.南盤江特大橋部分斜拉橋設計[J].橋梁建設，2009(5)：36-39.