一個具Logistic-型源和非線性信號產出的趨化系統解的漸近行為
宋芳芳, 陶有山
(東華大學 理學院,上海 201620)
趨化性是指細胞朝信號濃度變化大的地方遷移。除隨機擴散運動外,趨化性是生物世界中細胞遷移的最普遍機制之一,其在斑圖形成、細菌聚集和人口遷移等生物過程中起著極其重要的作用。經典的趨化數學模型在1970年由Keller和Segel[1]首次提出。數學上,該模型的一個顯著特征是:在多維空間情形下,解有可能在有限時間爆破。在過去的40多年里,趨化模型已被廣泛研究[2-3],其中,一些學者定性研究了交叉擴散、Logistic阻尼和非線性信號產出對解的性質的影響。本文考慮以下初邊值問題
(1)
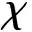
0≤g(s)≤sβ對所有的s≥0
(2)
式中:β為正常數。
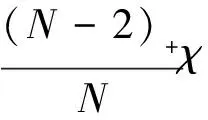
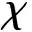
α>β
(3)
或者
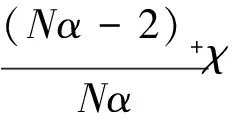
(4)
那么對任何給定的非負的u0∈W1,∞(Ω),初邊值問題(1)在Ω×(0,∞)上存在唯一且有界的整體古典解。
此外,文獻[5]通過構造上、下解的方法研究了解的長時間漸近行為。與文獻[5]不同,本文通過構造Lyapunov泛函方法,獲得了一個新解的漸近性結果。更精確地說,有如下結果:
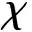

式中:M≥1為給定的常數。
時,該古典解u(x,t)具有下列漸近性質,即對所有的t>0, 式(5)和(6)成立。
‖u(·,t)-1‖L∞(Ω )≤Ce-λt
(5)
‖v(·,t)-1‖L∞(Ω )≤Ce-λt
(6)
式中:C>0,λ>0,且兩者為常數。
1 整體存在性和有界性
利用標準的不動點定理可證明系統(1)的局部解存在性,詳細證明參見文獻[3]。
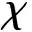
進一步,如果Tmax<∞,則有
下面的質量性質容易驗證。
引理2系統(1)的古典解(u,v)滿足
(7)
證明對系統(1)的第一個方程關于x在Ω上積分,并利用分部積分及系統(1)中的零流邊界條件可得
由H?lder不等式可得

再應用常微分方程比較原理推得式(7),引理2得證。
現在來推導一個基本的能量型不等式。
引理3對任何p>1,系統(1)的古典解(u,v)滿足:對所有的t∈(0,Tmax),式(8)成立。
(8)
證明根據系統(1)直接計算并利用分部積分,由條件式(2)和v的非負性得:
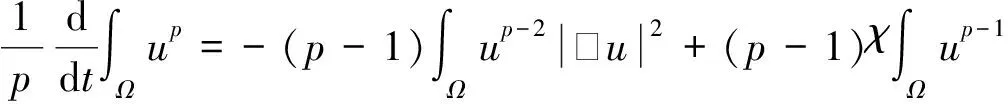
以式(8)為出發點,當α>β時可以建立u的Lp先驗估計。
引理4假設α>β,則對任何p>1,存在常數C(p)>0使得系統(1)的古典解滿足
(9)
證明由式(8)得到
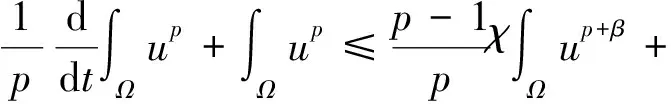
(10)
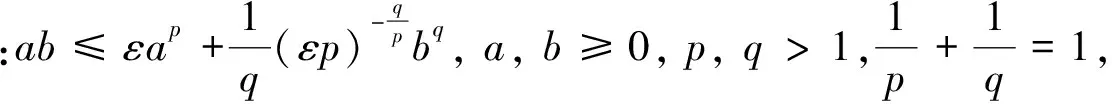

(11)
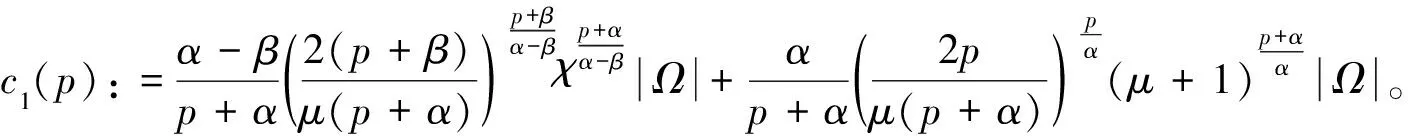
因此,如果取C(p):=c2(p),則式(9)得證。
當α=β時,對適當范圍的p可以建立u的Lp先驗估計。

(12)
證明由于假設α=β,由式(8)得
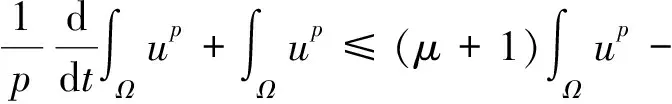
(13)
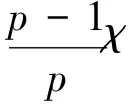
從而,利用Young不等式可知:
結合此不等式與式(13)得到
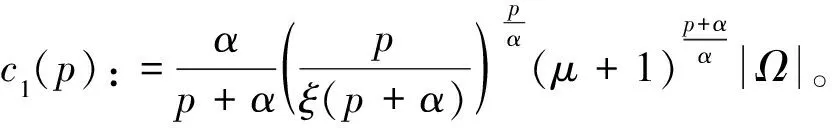
假設式(4)成立,以式(8)為基礎,利用引理5并結合Gagliardo-Nirenberg不等式也能建立u的Lp先驗估計。
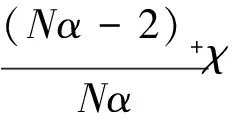
(14)
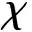
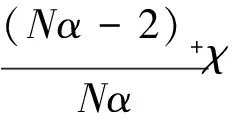
(15)
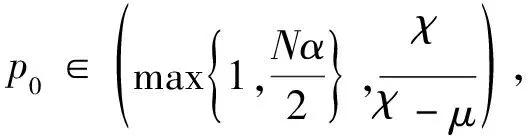
(16)
接下來,利用假設α=β,由式(8)和Young不等式得到:
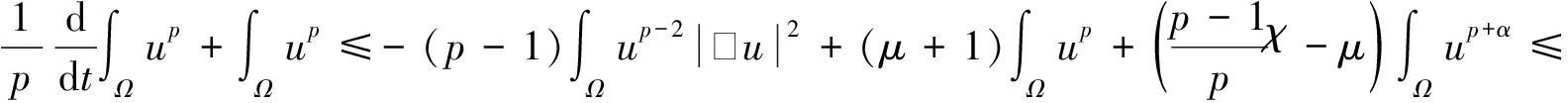
(17)
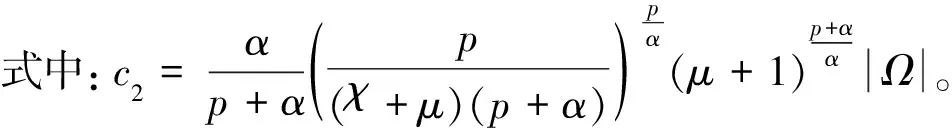

(18)
式中:
從而,由于p0的取法保證:2p0>Nα,因此有
據此并利用Young不等式可以進一步處理式(18)右端的第一項:
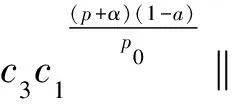
(19)
由式(17)~(19)得到
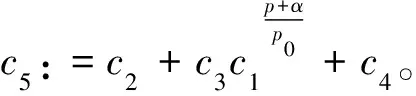
從而引理6得證。
由引理4和6并結合標準的Moser迭代技術,可證明u的有界性。
引理7假設定理1的條件成立,則存在常數C>0 使得系統(1)的古典解滿足
‖u(·,t)‖L∞(Ω )≤C, 對所有的t∈(0,Tmax)
(20)
證明在定理1的假設之下,由引理4和6得到:對任何p>1,存在常數c1(p)>0使得系統(1)的解滿足
(21)
據此并注意到式(2)這個假設,由系統(1)中的第二個橢圓方程及橢圓方程的正則性理論[8]可知:如果在式(21)中當p>N,則有
‖v(·,t)‖L∞(Ω )≤c2(p),t∈(0,Tmax)
(22)
獲得了估計式(21)和(22)之后,可以運用Moser迭代技巧推得式(20),詳細證明參見文獻[9]。
定理1的證明:定理1是引理1和7的直接推論。
2 解的漸近行為
本節重點討論解的長時間行為,將用到下列簡單的代數引理。
引理8設M≥1為常數,則對任何α>0,式(23)成立。
(s-1)(sα-1)≥K(s-1)2,
對所有的s∈[0,M]
(23)
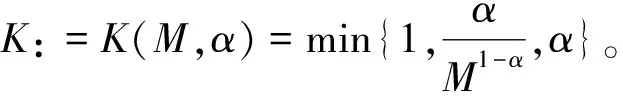
證明共分4種情形。
情形1α≥1,s≥1。在此情形下,顯然有
(s-1)(sα-1)≥(s-1)(s-1)=(s-1)2
情形2α≥1,0≤s<1。在此情形下,有
(s-1)(sα-1)=(1-s)(1-sα)≥
(1-s)(1-s)=(1-s)2
情形30<α<1,s≥1。在此情形下,由拉格朗日中值定理可知,存在ξ∈(1,s)?(1,M),使得
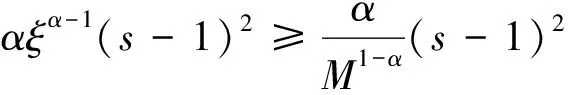
情形40<α<1,0≤s<1。在此情形下,再由拉格朗日中值定理可知,存在η∈(0,s)?(0,1),使得

即式(23)成立。
下列引理是研究有界古典解的漸近行為的關鍵,本質是構造了系統(1)的一個Lyapunov泛函。由于考慮有界解的長時間漸近性質,所以下文均可假設
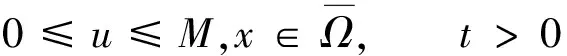
引理9假設g(s)=s,u0?0,則系統(1)的解滿足微分不等式:
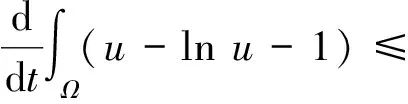
(24)
證明由于u0≡/ 0,所以由拋物方程的強最大值原理可知,當t>0時,u>0。利用系統(1)中的第一個方程進行直接計算,基于分部積分和基本不等式(23)得

(25)
再利用Young不等式進一步處理式(25)右端的第二項得

(26)
利用假設g(s)=s,將系統(1)中的第二個方程改寫成如下形式:
-Δv=-(v-1)+(u-1),x∈Ω,t>0
在上述方程兩邊同時乘以v-1之后,對x∈Ω積分,并再次利用Young不等式得
(27)
結合式(25)~(27)得:
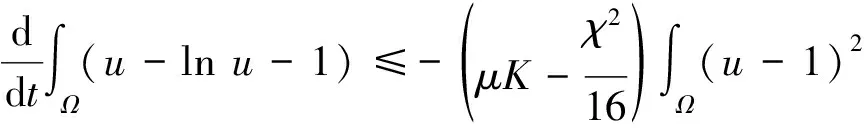
即式(24)成立。
由不等式(24)可以推出:當t→∞時,u(·,t)在L∞(Ω)中的收斂性。
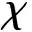
(28)
則系統(1)的解滿足
‖u(·,t)-1‖L∞(Ω )→0 當t→∞時
(29)
證明若式(28)中的假設成立,有
在上述不等式兩邊關于時間t在(1,t)上積分得

(30)
注意到:對任何s≥0,成立s-lns-1≥0,在式(30)中令t→∞,并結合式(28)有
(31)
得到了估計式(31)之后,接下來的證明與文獻[10]中的Lemma 3.10的證明類似。為便于理解,在此給出簡短證明。由于u是古典解,由拋物方程的Schauder理論[11]得到某個常數c1>0使得
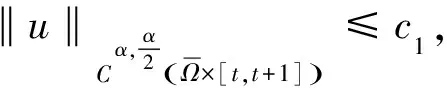
(32)

φ(xj,tj)≥c2, 對所有的j∈N
而式(32)意味著函數φ在Ω×[1,∞)上是一致連續的,因此可以找到小的常數r>0和τ>0使得對任何j∈N成立
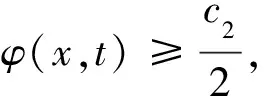
既然Ω的光滑性保證:存在某個常數c3>0,使得
|Br(x)∩Ω|≥c3, 對所有的x∈Ω.
據此推得
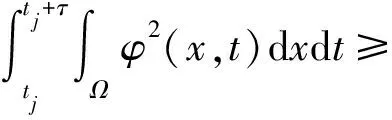
(33)
但另一方面,根據式(31)及廣義積分的收斂準則得到
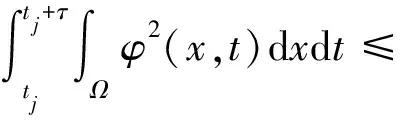
而這與式(33)矛盾,從而式(29)成立。
下面進一步研究解的收斂速率,先研究解在L2(Ω)中的收斂速率。
引理11假設g(s)=s,u0?0,并假設式(28)成立,則系統(1)的解滿足
‖u(·,t)-1‖L2(Ω )≤Ce-δt,t>0
(34)
式中:C>0,δ>0,且兩者均為常數。
證明首先注意到如下簡單事實
據此及式(29)可知,存在T>0充分大,使得
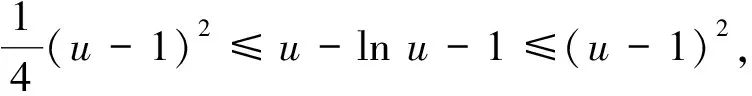
(35)
記
則利用不等式(24)和(35)得到
從而
據此并利用式(35)中左邊第一個不等式得到
如果取
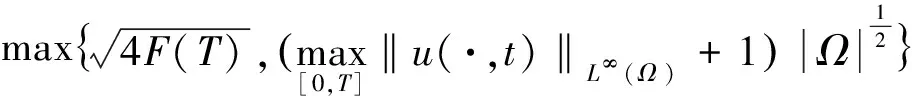
則式(34)成立。
然后討論解在L∞(Ω)中的收斂速率。
引理12假設g(s)=s,u0≡/ 0,并假設式(28)成立,則系統(1)的解滿足
‖u(·,t)-1‖L∞(Ω )≤Ce-λt,t>0
(36)
式中:C>0,λ>0,且兩者均為常數。
證明根據定理1及拋物方程的正則性理論可以找到某個常數c1>0滿足
‖u(·,t)-1‖W1,∞(Ω )≤c1,t>0
從而由引理11及Gagliardo-Nirenberg插值不等式可知:存在某個常數c2>0和c3>0使得

定理2的證明定理2中的式(5)是引理12的直接推論,而式(6)由式(5)及最大值原理推得。
參 考 文 獻
[1] KELLER E F, SEGEL L A. Initiation of slime mold aggregation viewed as an instability[J]. Journal Theoretical Biology, 1970, 26(3): 399-415.
[2] HILLEN T, PAINTER K. A users’ guide to PDE models for chemotaxis[J]. Journal of Mathematical Biology, 2009, 58(2): 183-217.
[3] BELLOMO N, BELLOUQUID A, TAO Y S, et al. Toward a mathematical theory of Keller-Segel models of pattern formation in biological tissues[J]. Mathematical Methods in the Applied Sciences, 2015, 25(9): 1663-1763.
[4] TELLO J I, WINKLER M. A chemotaxis system with logistic source[J]. Communications in Partial Differential Equations, 2007, 32(6): 849-877.
[5] GALAKHOV E, SALIEVA O, TELLO J I. On a parabolic-elliptic system with chemotaxis and logistic type growth[J]. Journal of Differential Equations, 2016, 261(8): 4631-4647.
[6] FRIEDMAN A. Partial differential equations[J]. Holt, Rinehart and Winston, 1969, 24(1):44-52.
[7] WINKLER M. A critical exponent in a degenerate parabolic equation[J]. Mathematical Methods in the Applied Sciences, 2002, 25(11): 911-925.
[8] GILBARG D, TRUDINGER N S. Elliptic partial differential equations of second order[J]. Springer Verlag, 1983, 224(3): 469-484.
[9] TAO Y S, WINKLER M. Boundedness in a quasilinear parabolic-parabolic Keller-Segel system with subcritical sensitivity[J]. Journal of Differential Equations, 2012, 252(1): 692-715.
[10] TAO Y S, WINKLER M. Large time behavior in a multidimensional chemotaxis-haptotaxis model with slow signal diffusion[J]. SIAM Journal on Mathematical Analysis, 2015, 47(6): 4229-4250.
[11] PORZIO M M, VESPRI V. H?lder estimates for local solutions of some doubly nonlinear degenerate parabolic equations[J]. Journal of Differential Equations, 1993, 103(1): 146-178.

