尺規作圖題的歸類解析
文 /朱廣科

縱觀近幾年的中考作圖題,已不局限于對基本作圖技能的考查,取而代之的是設計新穎、富有創意的作圖題.現把各種題型歸類如下,供你復習時參考.
一、基本作圖型
例1 如圖1,A,B,C為某公園的三個景點,景點A和景點B之間有一條筆直的小路,現要在小路上建一個涼亭P,使景點B、景點C到涼亭P的距離之和等于景點B到景點A的距離,請用直尺和圓規在所給的圖中作出點P.(不寫作法和證明,只保留作圖痕跡)
解:如圖1,連接AC,作線段AC的垂直平分線MN,直線MN交AB于P.

圖1
點P即為所求的點.
點評:尺規作圖是指用無刻度的直尺和圓規來作圖,通常稱為基本作圖.解尺規作圖題時,要明確直尺和圓規的功能.理解圖形的本質特征,確定作圖順序是解題的關鍵,一定要保留作圖痕跡.
二、圖形剪拼型
例2七巧板是我國祖先的一項卓越創造.下列四幅圖中有三幅是小明用如圖2所示的七巧板拼成的,則不是小明拼成的那幅圖是( )

圖2

解:根據勾股定理,可判斷邊長之間的關系,不能構成C圖案,能構成A,B,D圖案.
選C.
點評:解答剪拼問題需要邏輯推理,要多方位、多角度、多層次地探索,觀察拼接前后的圖形,根據它們的邊、角、面積之間關系確定正確選項.
三、圖形變換型
例3在圖3和圖4中,4×4網格圖都是由16個相同小正方形組成,每個網格圖中有4個小正方形已涂上陰影,請在空白小正方形中,按下列要求涂上陰影.
(1)在圖3中選取2個空白小正方形涂上陰影,使6個陰影小正方形組成一個中心對稱圖形;
(2)在圖4中選取2個空白小正方形涂上陰影,使6個陰影小正方形組成一個軸對稱圖形,但不是中心對稱圖形.

圖4
解:(1)選取2個小正方形涂上陰影(新涂的陰影用灰色表示),使6個陰影正方形成中心對稱圖形,如圖5所示.
(2)選取2個小正方形涂上陰影(新涂的陰影用灰色表示),使6個陰影小正方形成軸對稱圖形,但不是中心對稱圖形,如圖6所示.

圖5

圖6
點評:圖形變換主要包括圖形的平移、翻折、旋轉等幾種情況.解題的關鍵是觀察圖形并挖掘其中的變換條件,根據變換的性質確定圖形的位置.
四、利用網格的特征作圖
例4圖7、圖8、圖9都是由邊長為1的小等邊三角形構成的網格,每個小等邊三角形的頂點稱為格點.線段AB的端點在格點上.
(1)在圖7、圖8中,以AB為邊各畫一個等腰三角形,且第三個頂點在格點上(所畫圖形不全等);
(2)在圖9中,以AB為邊畫一個平行四邊形,且另外兩個頂點在格點上.
解:(1)根據等腰三角形的定義作圖,以AB為底,△ABC為所求,如圖7,以AB為腰,△ABD為所求,如圖8.
(2)根據平行四邊形的判定定理作圖,如圖9所示,?ABCD即為所求.

圖7

圖8

圖9
點評:以三角形網格為背景的作圖題,不需要繁雜的計算和證明,憑借格點的特征,復雜的位置問題變得簡單而生動.利用網格線平行的結構特征,結合等腰三角形、平行四邊形的性質等,就能準確找出對應點的位置.
五、開放探究型
例5在平面直角坐標系中,我們把橫、縱坐標都為整數的點稱為整點,記頂點都是整點的三角形為整點三角形.如圖10,已知整點A(2,3),B(4,4),請在網格區域(含邊界)按要求畫整點三角形.
(1)在圖10中畫一個△PAB,使點P的橫、縱坐標之和等于點A的橫坐標;
(2)在圖11中畫一個△PAB,使點P,B橫坐標的平方和等于它們縱坐標和的4倍.
解:(1)設P(x,y),由題意x+y=2,
∴ P(1,1)或(2,0)或(0,2),但(0,2)不構成三角形,舍去,
△PAB,△P′AB符合題意,如圖10所示.
(2)設P(x,y),由題意得x2+42=4(4+y),x=2,y=1,符合題意,可得整點(2,1),△PAB符合題意,如圖11所示.
點評:分類討論是解題的關鍵.分類時,要認真思考,做到不重復不遺漏.

圖10

圖11
六、閱讀理解型
例6直角在初中幾何學習中無處不在.
如圖12,已知∠AOB,請仿照小麗的方式,再用兩種不同的方法判斷∠AOB是否為直角(僅限用直尺和圓規).
小麗的方法:如圖13,在OA,OB上分別取點C,D,以C為圓心,CD長為半徑畫弧,交OB的反向延長線于點E,若OE=OD,則∠AOB=90°.
解:方法1:如圖14,在OA,OB上分別截 取 OC=4,OD=3, 若 CD=5,則∠AOB=90°.

圖12

圖13
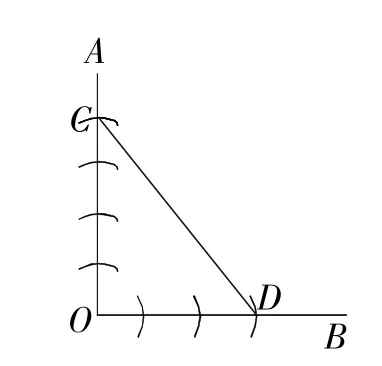
圖14

圖15
方法2:如圖15,在OA,OB上分別取點C,D,以CD為直徑畫圓.若點O在圓上,則∠AOB=90°.

