優化解題方法體會數學本質

程亞芳

(江蘇省江陰中等專業學校 214400)

對于學生而言，最重要的數學教學恰是解題教學．本文以經典問題與讀者交流，指出優化解題方式，引導學生體會問題背后的數學本質．

一、避開分類追求本質

問題1t為常數，函數y=|x2-2x-t|在[0,3]上的最大值為2，則________．

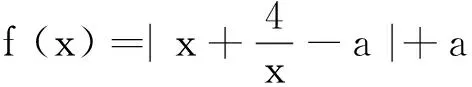
分析上述兩個絕對值函數的最值問題，是經典的絕對值幾何意義的體現．不妨請學生先嘗試一下，很容易發現幾乎所有學生都是分類討論，筆者也曾經聆聽一位教師在公開課上將這樣的問題，分組請學生討論、演算，最終獲得結果，非常耗時耗力．筆者想說，其實這樣的教學是毫無意義的！因為，這種分類討論的解題方式，根本就不是該問題考查的本質！

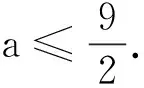
體會分類討論是一種基本問題的解決思路，但是一味的分類討論往往陷入了模式識別的“陷阱”，讓思維變得僵化，也失去了該問題本質的挖掘機會．結合數學思想，絕對值幾何意義才是我們解該題的最好方式，通過這樣的方式體會了絕對值幾何意義的本質——數值上點之間的距離．

二、合理工具尋求本質

好的問題不僅具備知識的整合性，也體現了考查的區分度．眾所周知，解析幾何中向量工具的重要性不言而喻．作為向量章節而言，最為核心的知識莫過于平面向量數量積和平面向量基本定理，若能用好這兩個向量知識的本質，對于問題的解決會有豁然開朗的視角．

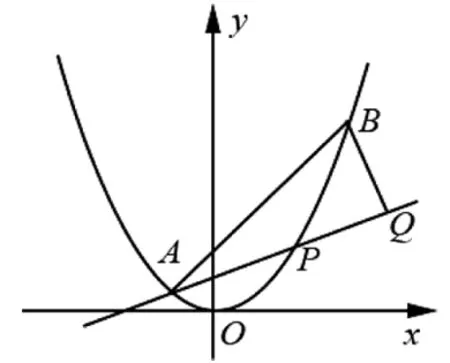
圖1

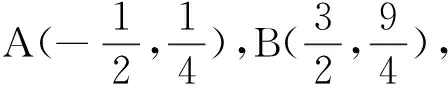
回顧：研究第(2)問題，參考答案是這樣給出的：

聯立直線AP和BQ的直線方程，

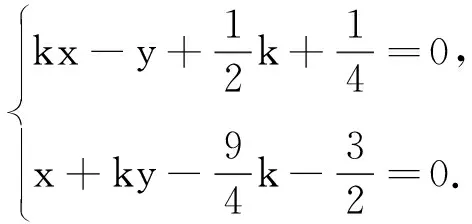
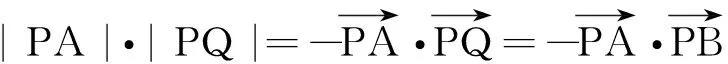
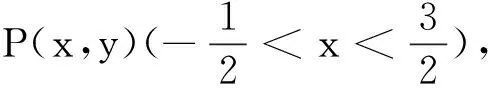
體會：理解設而不求，因此利用垂直滲透向量數量積投影的特性，將問題解決的最優方式呈現出來，以體會向量的作用．

總之，對于數學問題的選擇需要有深刻的意義，而不是就題論題，更不能只做不思，要從最合適的解法中尋求真正的凸顯數學本質的解題方法，才是數學教學的意義．

參考文獻：

[1]殷偉康.數學概念教學中追問的特征與時機[J].數學教學研究,2014(5).

[2]吳志雄.培養高中生數學本質的策略與思考[J].中學數學研究,2016(5).

[3]王珂.從一個教材問題思考課堂教學的深度[J].數學教學研究,2015(9).