高考試題中的空間線線角

蘇藝偉

(福建省龍海第一中學新校區 363100)

立體幾何是高中數學主干知識,它緊緊圍繞數量關系,空間形式，數形結合,公理化思想這4條主線,讓學生有機會體會和認識一些數學本源性問題.其中的空間角是高考重點考查的內容,包括線線角,線面角,面面角.求解空間角一般可以采用綜合法和向量法(包括向量基底法和向量坐標法).本文以求解空間中的線線角為例進行說明.

求解空間中的線線角一般可以采用以下方法.

方法1：綜合法

立體幾何問題解決的基本策略是立體問題平面化.綜合法以公理,定理體系為理論基礎,對空間中的點,線,面的關系從形上去認識,根據判定定理與性質定理把空間的線線,線面,面面關系通過傳遞轉化為平面內的線線關系,具有逐步過渡,步步為營,推理嚴謹,簡潔明了等特點.而借助輔助線的定位過渡是解題的難點與關鍵,需要學生構建整體觀念和具有一定的平面幾何基礎.

方法2：向量法

向量法的實質是幾何問題代數化(將幾何問題轉化為數量問題進行量化處理),把立體幾何從形向數上延伸,用代數運算的方式解決立體幾何問題,運算公式植根于綜合法,具有跨越定位過程,隔空傳遞,關注結果,化繁為簡,操作容易等特點.

例1 (2017年全國Ⅱ卷)

已知直三棱柱ABC-A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1,則異面直線AB1與BC1所成角的余弦值為( )

方法1：綜合法

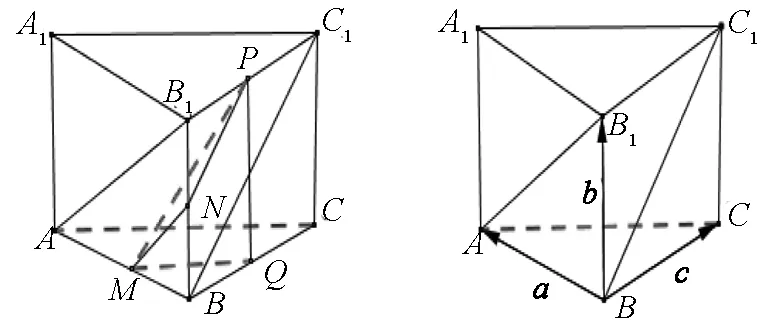
圖1 圖2

如圖1所示,取AB中點M,BC中點Q,B1B中點N,B1C1中點P，連結MQ,PQ,MP,MN,PN.由于AB1∥MN,BC1∥PN,所以異面直線AB1與BC1所成的角即為∠MNP或其補角.

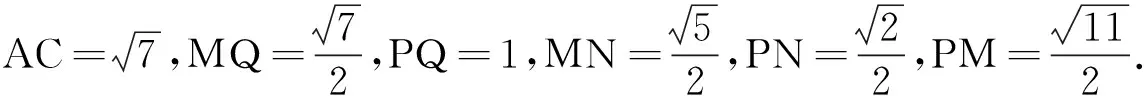
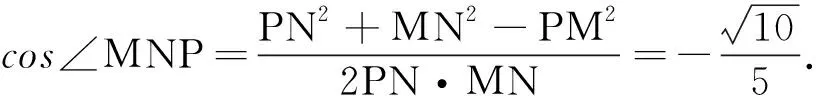
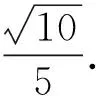
方法2：基底法

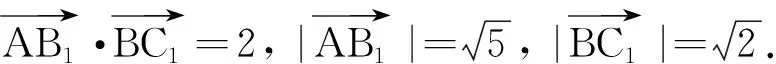
設異面直線AB1與BC1所成的角為θ,則cosθ=

方法3:坐標法

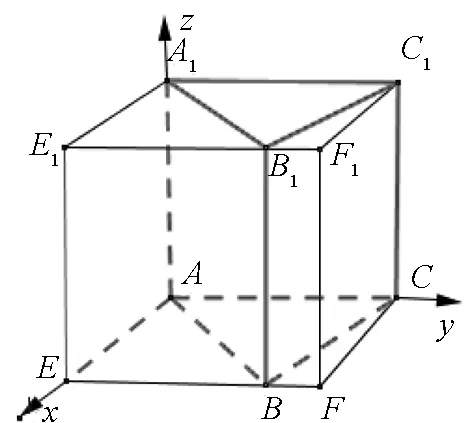
圖3

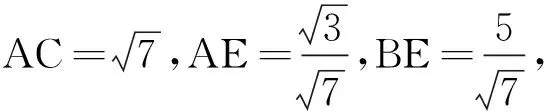
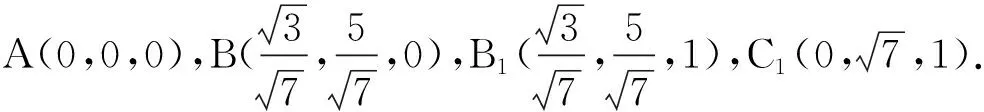
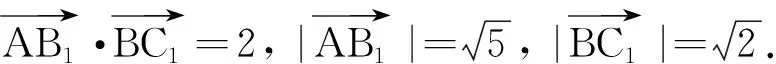
設異面直線AB1與BC1所成的角為θ,則cosθ=

例2 (2015年浙江卷)

在三棱錐A-BCD中,AB=AC=BD=CD=3,AD=BC=2,點M,N分別為AD,BC的中點,則異面直線AN,CM所成角的余弦值是________.

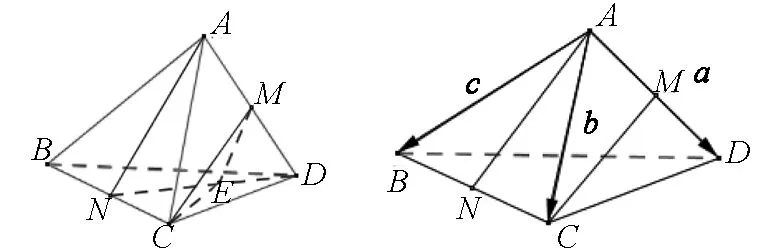
圖4 圖5

方法1：綜合法

如圖4所示,連結DN,取DN中點E,連結ME,CE.

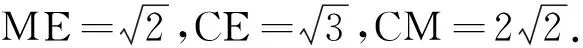
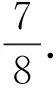
方法2：基底法

如圖5所示,

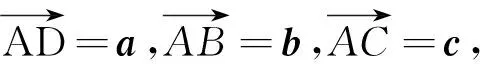
|c|=3.

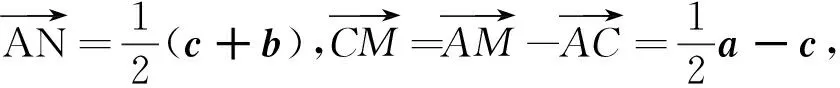
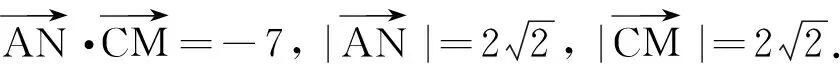
設異面直線AN與CM所成的角為θ,則cosθ=

方法3：坐標法

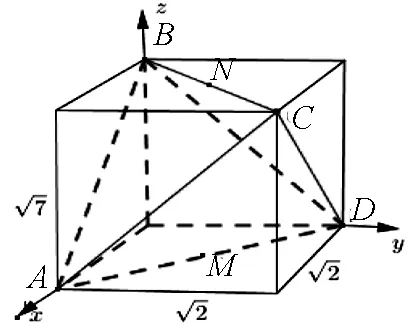
圖6

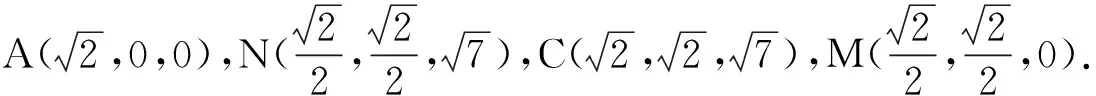
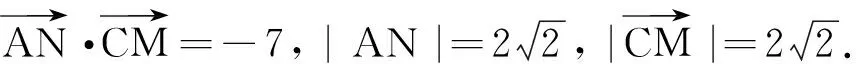
設異面直線AN與CM所成的角為cosθ=

上述兩種方法是處理空間中兩直線所成角的常用方法.方法1為綜合法,理論依據是立幾中的三個公理以及相關定理,性質.其關鍵在于作出輔助線,進而證實與解答.方法2是基底法,理論依據是空間向量基本定理(空間中任意一個向量都可以表示成不共面的三個向量的線性組合),需要三個模與相互夾角已知的不共面向量作為基底,用其表示空間內任意向量,通過數量積等運算實現化歸.方法3是建立空間直角坐標系,將幾何元素以坐標的形式體現出來,轉化為坐標的運算.三種方法都具有各自的優點,不可偏廢.在實際解題中我們應該要靈活根據題目條件選擇合適的方法以期達到最優化效果.

例3 (2014年新課標全國卷Ⅱ)

直三棱柱ABC-A1B1C1中,∠BCA=90°,M,N分別是A1B1,A1C1中點,BC=CA=CC1,則BM與AM所成角的余弦值為( )

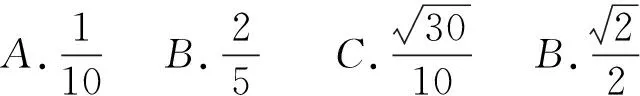
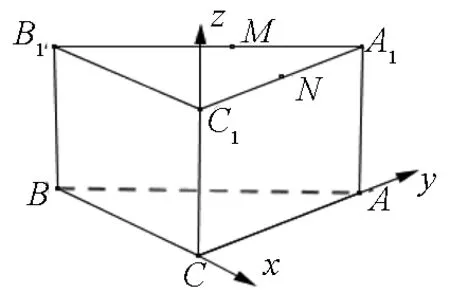
圖7

解析如圖7所示,以C為原點建立空間直角坐標系.

設BC=CA=CC1=2,則A(0,2,0),N(0,1,2),B(-2,0,0),M(-1,1,2),

設異面直線BM與AN所成的角為θ,則cosθ=

例4 (2014年大綱卷第11題)

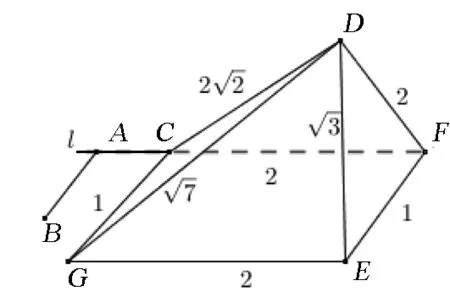
圖8

已知二面角為α-l-β為60°,AB?α,AB⊥l,A為垂足,CD?β,C∈l,∠ACD=135° ,則異面直線AB與CD所成角的余弦值為 ( )

其中結論正確的是________.

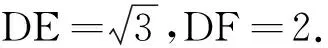
例5 (2017年全國Ⅲ卷)

設a,b為空間中兩條互相垂直的直線,等腰直角三角形ABC的直角邊AC所在直線與a,b都垂直,斜邊AB以直線AC為旋轉軸,有以下結論:

(1)當直線AB與α成60°角時,AB與b成30°角.

(2)當直線AB與a成60°角時,AB與b成60°角.

(3)直線AB與a所成角的最小值為45°.

(4)直線AB與a所成角的最大值為60°.

其中結論正確的是____.

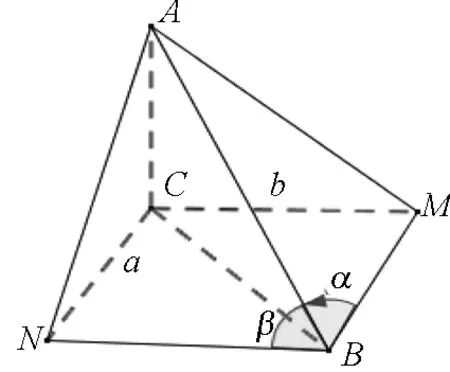
圖9

解析如圖9所示,設直線a為直線NC,直線b為直線MC,設直線AB與a所成的角為α,直線AB與b所成的角為β.

作BM∥C,BN∥MC,則α=∠ABM,β=∠ABN.

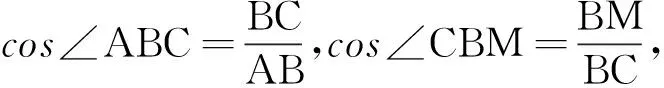
因此有cosα=cos∠ABC·cos∠CBM,

(1)

cosβ=cos∠ABC·cos∠CBN=cos∠ABC·sin∠CBM.

(2)

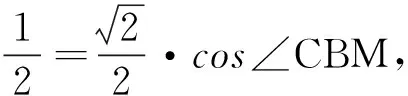
所以當直線AB與α成60°角時,AB與b成60°角.第(2)個正確.

又因為斜線與射影所成的角是該斜線與平面內任意 一條直線所成角中最小的,故直線AB與a所成角的最小值為45°.第(3)個正確.

評析上述三道試題從圖形特征以及待求目標來看,采用向量法顯然不合適,因此采用綜合法進行求解.

空間中的線線角折射出學生對綜合法與向量法的理解,在實際教學中,要正確處理好綜合法與向量法的運用關系,不能顧此失彼.筆者認為,在高三一輪復習時，要強調使用幾何法，以鞏固定理，規范證明過程書寫，提高推理論證能力.在高三二輪復習時,要讓學生根據實際,靈活選擇以實現簡化解題過程之目的.

參考文獻：

[1]李波.2017年高考立體幾何專題解題分析[J].中國數學教育,2017(7-8):113-117.