基于Wiener過程的發動機多階段剩余壽命預測

黃亮， 劉君強， 貢英杰

(南京航空航天大學 民航學院， 南京 211106)

發動機的失效是材料處于惡劣的運行環境下緩慢退化的結果[1-2]。隨著系統復雜程度的提高，傳統基于失效機理模型的方法很難構建出可靠的故障模型來對應產品的失效過程[3-4]。基于統計性能退化監測數據的方法只需要運行過程中產生的退化數據，不必建立精確的數學模型，具有較高的計算優勢。

目前，基于統計性能退化監測數據的壽命預測是研究的熱門[5-6]，并且已經研究出多種性能退化模型，例如隨機系數模型[7]、隨機過程模型[8-9]和隨機濾波模型[10]等。基于統計性能退化監測數據的壽命預測方法，利用退化過程的隨機性求出剩余壽命的概率分布情況，便于反映預測結果的隨機性。在基于隨機過程模型中，最常采用Wiener過程。Wiener過程便于描述系統因受到外部環境影響、內部的狀態改變以及負載情況，而具有隨機的非單調獨立增量過程[11]。由于Wiener過程可以用來描述隨機的非單調獨立增量過程，目前大量采用Wiener過程對復雜系統進行性能退化建模[12]。通常所說的Wiener過程是指具有線性漂移系數的一類隨機過程[13-14]。Wang[15]提出了基于期望最大化(Expectation-Maximization，EM)算法的性能退化模型參數估計方法。

上述研究豐富了Wiener過程在剩余壽命預測領域中的應用，但還存在著如下幾個問題：

1) 假設系統的性能退化過程是關于時間的線性函數，或運用某些尺度轉換方法將非線性關系轉化為線性關系[16]。例如Gebraeel[17]采用取對數方法將指數退化模型轉變為一般的線性退化模型。然而，還有很多非線性退化過程無法轉換為線性的，例如航空發動機性能退化過程具有明顯的非線性特點，直接建立非線性退化模型更滿足實際情況。司小勝等[18]采用非線性Wiener過程對復雜系統的剩余壽命進行研究。

2) 在目前的剩余壽命預測研究中，鮮有研究多階段退化的情況。劉君強等[19]在發動機的壽命預測中研究了多階段的情況，實驗結果表明發動機的退化過程具有多階段性。

3) 如何體現個體性能退化的差異性。由于環境、材料和誤差等的影響，同類型產品的性能退化過程存在差異性，在產品的剩余壽命預測中需要考慮個體性能退化的差異性。劉君強等[19]提出性能退化模型參數具有隨機性，服從高斯-伽馬分布，從而反映出個體退化的差異性。

針對以上問題，本文根據航空發動機性能退化具有非線性、多階段的性質，用多階段非線性Wiener過程構建出性能退化模型。根據多個同類產品歷史性能退化監測數據，利用極大似然估計與一維搜索方法，進行參數先驗分布的估計，在先驗分布和實時獲取的個體發動機退化數據的基礎上，用貝葉斯方法求得參數的后驗分布，從而實現對個體發動機剩余壽命的實時精確預測。

1 剩余壽命預測模型

1.1 模型分析與假設

通過分析航空發動機具有復雜多階段非線性的性能退化特點，本文將采用多階段非線性的Wiener過程建立性能退化模型。在該非線性Wiener過程中漂移系數不再與時間無關，而是關于時間的非線性函數。基于非線性Wiener過程的性能退化模型可以表示為

(1)

式中：X(t)為在時刻t的性能退化量；u(t;θ)為非線性Wiener過程的漂移系數，θ為漂移系數的非線性函數中的未知參數；σ為擴散系數；B(t)為標準布朗運動。當u(t;θ)=u時，上述非線性性能退化模型轉化為一般線性Wiener退化模型。

為了通過實際發動機監測數據進行實例的驗證,根據文獻[8]，本文假設u(t;θ)=urtr-1，此時的非線性退化模型變為

X(t)=utr+σB(t)

(2)

式中：r為漂移系數的非線性函數中的未知參數。

利用Wiener過程進行多階段非線性的退化建模需要做出以下假設:

假設1當性能退化量沒有超過失效閾值時，發動機處于正常狀態；超過失效閾值時，則發動機處于失效狀態。

假設2為描述航空發動機性能退化的個體差異性，將模型參數u,σ2視為隨機變量，設w=1/σ2,可得u,w的聯合分布是高斯-伽馬分布：

(3)

式中：a、b、c、d為u和w組成的聯合分布中的參數。

1.2 多階段性能退化模型

多階段的性能退化模型可以表示為

X(t)=(X(0)+X1(t))I(0,t1)(t)+(X(t1)+

X2(t-t1))I(t1,t2)(t)+…+(X(tn-1)+

Xn(t-tn-1))I(tn-1,∞)(t)

(4)

式中：I(t)為示性函數；X(0)為性能退化模型的初始值；X(ti)為ti時的性能退化值，ti為到達每個性能退化分界值的時間；Xn(t-tn-1)為第n階段的退化函數。

根據1.1節分析與假設，本文將使用多階段非線性的Wiener隨機過程構建出性能退化模型。此時，X(t)表示為

X(t)=(u1tr1+σ1B(t))I(0,t1)(t)+[W1+

u2(t-t1)r2+σ2B(t-t1)]I(t1,t2)(t)+…+

[Wn-1+un(t-tn-1)+σnB(t-tn-1)]·

I(tn-1,∞)(t)

(5)

式中：Wn-1為第n-1個性能退化階段的分界值。

1.3 壽命分布

剩余壽命Lt′定義為產品自t′時的退化量X(t′)到其第一次超出失效閾值Wn所用的時間，剩余壽命Lt′表達式為

Lt′=inf{X(t+t′)≥WnX(t′)≤Wn}=

inf{X(t+t′)-X(t′)≥Wn-X(t′)}

(6)

式中：X(t′)和X(t+t′)分別為在t′和t′+t時刻的性能退化量；Wn為失效閾值。

因為本文構建的退化模型考慮了非線性的性質，很難計算求得Lt′的準確分布。為此，Si等[8]給出了剩余壽命概率密度函數的一個近似表達式。航空發動機的剩余壽命Lt′的概率密度函數為

(7)

1.4 剩余壽命預測的多階段性

令ξk為航空發動機性能退化量X(t)從初始時刻到其第一次超過第k個性能退化階段分界值Wk的時間，ξk為

ξk=inf{t:X(t)≥Wk,t>0}

(8)

根據Wiener過程的齊次馬爾可夫性質，則ξk可以改寫為

ξk=ξk-1+inf{t:X′(t)≥Wk-Wk-1,t>0}

(9)

式中：X′(t)為第k個階段的性能退化模型；X′(t)=uktrk+σkB(t)，其中uk、rk和σk表示第k個階段性能退化模型的參數。

令Δξk=ξk-ξk-1，ΔWk=Wk-Wk-1，則式(9)可以改寫為

Δξk=inf{t:X′(t)≥ΔWk,t>0}

(10)

根據式(7)可得第k個性能退化階段的壽命分布函數為

(11)

由式(11)可以推導出航空發動機壽命T為

T=Δξ1+Δξ2+…+Δξn

(12)

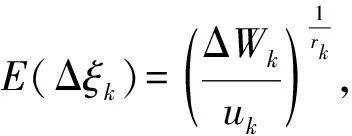
(13)

當t′時刻的性能退化量X(t′)滿足要求X(ξk-1)≤X(t′)≤X(ξk)，Lt′表達式為

Lt′=(ξk-t′)+Δξk+1+…+Δξn

(14)

2 參數估計

由于很難直接估算出未知超參數a、b、c和d的值，本文將采用兩階段方法進行估計。首先，根據現有的航空發動機的歷史退化監測數據，利用極大似然估計與一維搜索方法估算出一組u,σ2的值。然后，根據估算出的一組u,σ2的值，再利用極大似然估計方法估算出a、b、c和d的值。

2.1 第1階段參數估計

假設現在共有m個同類型的航空發動機的性能退化監測數據，其中第i個發動機的第k個階段的監測時刻記為tik1,tik2,…,tikn，與此時刻相對應的性能退化監測數據記為yik1,yik2,…,yikn。

(15)

式中：yikj為第i個發動機在第k個階段的第j次監測值；tik-1為第i個發動機到達第k-1個階段分界值的時間；nik為第i個發動機在第k個階段的監測次數；tikj為第i個發動機在第k個階段的第j次監測時間。

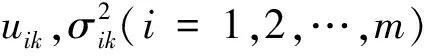
(16)

根據式(15)進一步可求得m個航空發動機的退化模型參數Θ=[uik,rik,σik]的完全對數似然函數為

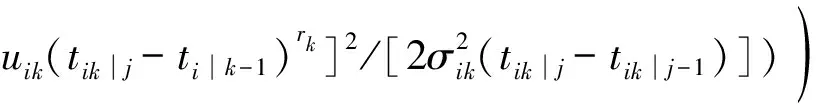
(17)

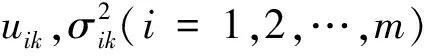
2.2 第2階段參數估計

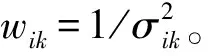
l(ak,bk,ck,dkuik,wik)=

(18)

極大化l(ak,bk,ck,dkuik,wik)，求得估計值為

(19)

3 基于貝葉斯方法的模型參數更新

由于材料、環境等外界因素的影響，同一型號發動機的性能退化路徑存在著個體的差異性。ΔYk=(Δy1,k,Δy2,k,…,Δyn,k)為個體發動機處于第k個退化過程的監測數據。

當獲得個體發動機實時性能退化數據后，根據貝葉斯方法可得第k個性能退化階段的參數uk和wk的后驗分布為

f(uk,wkΔYk)∝l(ΔYkuk,wk)f(uk,wk)

(20)

式中：f(uk,wkΔYk)為個體發動機第k性能退化階段模型參數的后驗分布函數；f(uk,wk)為第k性能退化階段的模型參數uk和wk的先驗分布函數；l(ΔYkuk,wk)為似然函數。

根據文獻[20]中共軛先驗分布的性質，個體發動機第k個性能退化階段中的模型參數uk和wk更新后的后驗分布表達式為

(21)

式中：

(22)

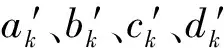
由于參數u和w的聯合分布是高斯-伽馬分布，更新后的uk和wk的后驗分布期望為

(23)

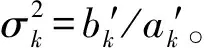
4 個體發動機的實時剩余壽命預測

根據發動機的歷史性能監測數據和單臺發動機的實時監測數據，建立多階段航空發動機性能退化模型。首先利用極大似然估計和一維搜索方法，進行參數先驗分布的估計。在先驗分布和實時獲取的個體發動機退化數據的基礎上，采用貝葉斯方法對參數分布更新。從而實現對個體發動機剩余壽命的實時精確預測。剩余壽命預測的具體步驟如圖1所示。

步驟1基于歷史性能退化數據，根據式(14)建立退化模型的對數似然函數，利用極大似然與一維搜索方法估算出模型參數的先驗分布。

步驟2當獲取到個體發動機的實時性能退化監測數據后，運用貝葉斯方法，根據式(20)～式(22)對發動機性能退化模型參數進行實時更新。

步驟3根據式(23)可以求得發動機性能退化模型中的參數u,σ2的后驗分布的期望估計值。

步驟4根據式(11)～式(14)多階段非線性Wiener過程的壽命預測方法，求得個體發動機實時的剩余壽命。

5 實例驗證

排氣溫度裕度(Exhaust Gas Temperature Margin，EGTM)是監測發動機性能的關鍵指標。7臺同類型的航空發動機在全壽命周期內監測的EGTM數據如表1所示。為了驗證多階段非線性Wiener過程在航空發動機剩余壽命預測中的準確性，選擇表1中前5臺發動機的EGTM歷史監測數據用作先驗參數估計，后2臺發動機的EGTM監測數據用作實時更新。根據經驗，EGTM的失效閾值定義為0℃。

圖2給出了該7臺發動機的性能退化路徑。從圖中可知，在大于35℃時，EGTM的上升速度較慢，0～35℃時，EGTM的退化速度較快。將發動機的退化分界值定義為ξ=35℃。此時，可采用兩階段非線性的Wiener過程進行退化建模。

根據表1中給出的航空發動機歷史EGTM監測數據，利用極大似然估計方法和一維搜索方法，即可得到發動機性能退化模型各階段參數先驗分布的估計值，超參數的估計結果如表2所示。

表1某型號發動機EGTM監測數據

Table1EGTMmonitoringdataofacertainmodelofengine

當前時間/cycle發動機編號12345671006970.8746767616920063.356.2706561.465.363????????360021.6198-0.31513.919.4370018.717.15.610.412.516.538009.516.4-0.112.86.813.639001.210.4-0.910.74000-0.86.8

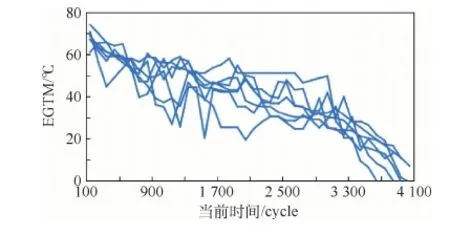
圖2 航空發動機退化路徑Fig.2 Degradation path of aeroengines

從圖2中可知，該型號發動機在不同階段的退化速率存在著明顯的差異，進一步說明了發動機的退化過程具有多階段的特點。

在計算求得航空發動機各階段性能退化模型參數的先驗分布后，可以運用貝葉斯方法，基于實時性能退化數據對模型參數的后驗分布進行更新。以編號為6的發動機為例，在獲得實時性能退化監測數據后，經貝葉斯更新后的模型參數第1階段和第2階段估計結果分別如表3和表4所示。

在得到了參數更新后的估計值后，可以對發動機性能退化各階段的剩余壽命進行實時預測。

圖3和圖4分別給出了編號為6的航空發動機在第1和第2階段的實時剩余壽命概率密度分布圖。

為直觀反映出基于多階段非線性Wiener的退化模型與傳統的單階段線性Wiener隨機過程在壽命預測問題中的精確性，定義相對誤差(Relative Error,RE)指標為

(24)

式中：L為預測剩余壽命；T為實際剩余壽命。

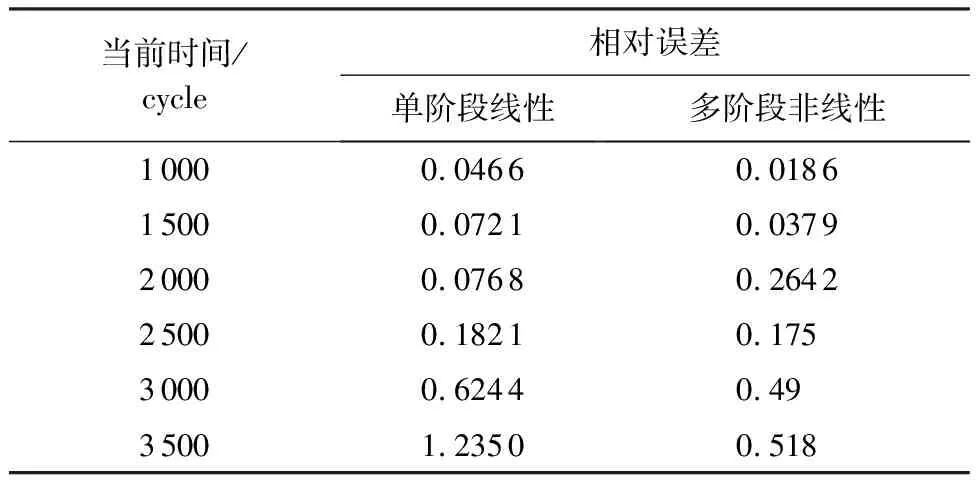
2種模型的相對誤差計算結果如表5所示。

根據表5的相對誤差對比結果，可計算得到單階段線性與多階段非線性的平均誤差分別為0.372 8和0.2506。基于多階段非線性Wiener過程的剩余壽命預測平均誤差值小于傳統的預測，證實本文方法用于航空發動機剩余壽命預測的結果更精確。產生以上誤差對比結果的原因是航空發動機性能退化具有多階段非線性特點，基于多階段非線性Wiener過程構建的性能退化模型更加符合實際航空發動機的性能退化路徑。此外，同類型發動機由于環境和材料等因素的影響會產生個體的差異性，考慮個體差異性的航空發動機剩余壽命預測結果更加精確。

表2 超參數的先驗估值

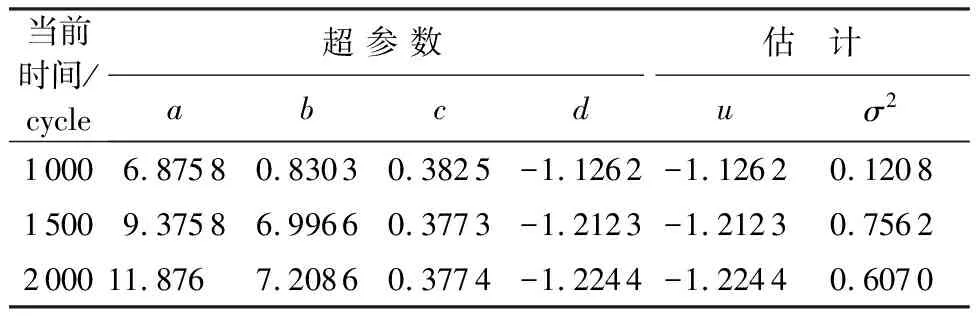
表3 貝葉斯更新后的參數第1階段估計結果

表4貝葉斯更新后的參數第2階段估計結果

Table4Bayesupdatedparameterestimationresultsatthesecondstage

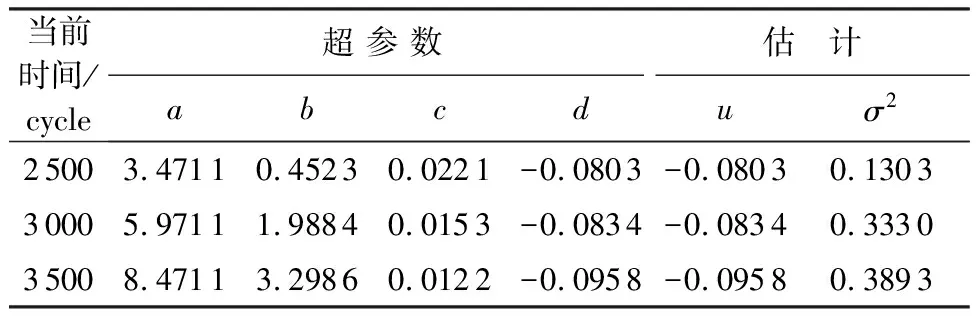
當前時間/cycle超 參 數估 計abcduσ225003.47110.45230.0221-0.0803-0.08030.130330005.97111.98840.0153-0.0834-0.08340.333035008.47113.29860.0122-0.0958-0.09580.3893

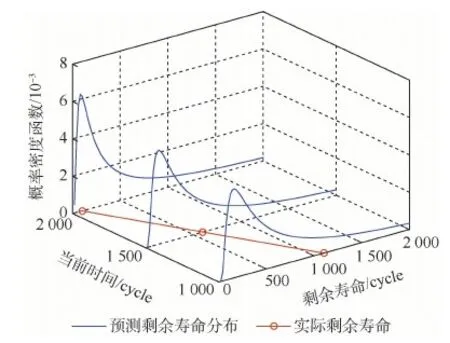
圖3 第1階段剩余壽命概率密度分布Fig.3 Probability density distribution of residual life at the first stage

圖4 第2階段剩余壽命概率密度分布Fig.4 Probability density distribution of residual life at the second stage

當前時間/cycle相對誤差單階段線性多階段非線性10000.04660.018615000.07210.037920000.07680.264225000.18210.17530000.62440.4935001.23500.518

6 結 論

1) 本文采用了基于多階段非線性的Wiener過程來建立航空發動機的性能退化模型，能夠較好地滿足航空發動機的實際退化路徑。

2) 與不考慮個體差異的Wiener過程的性能退化模型相比，考慮個體差異性的Wiener過程更能描述復雜系統的退化過程，剩余壽命的估算結果更加的準確。

3) 當獲取個體發動機的實時監測數據后，能夠結合歷史性能退化監測數據，運用貝葉斯方法對模型參數的后驗分布進行實時更新，實現對個體發動機剩余壽命的實時精確預測。

參考文獻 (References)

[1] PECHT M G.Prognostics and health management of electronics[M].Hoboken：Wiley Online Library,2008:1-19.

[2] GUAN Q,TANG Y,XU A.Objective Bayesian analysis accelerated degradation test based on Wiener process models[J].Applied Mathematical Modelling,2016,40(4):2743-2755.

[3] 謝吉偉,劉君強,王小磊.應用交互式多模型算法的設 備剩余壽命預測[J].空軍工程大學學報(自然科學版),2016,17(2):98-102.

XIE J W,LIU J Q,WANG X L.A residual usefual lifetime prediction based on interacting multiple model algorithm[J].Journal of Air Force Engineering University(Natural Science Edition),2016,17(2):98-102(in Chinese).

[4] SI X S,WANG W,HU C H,et al.Remaining useful life estimation—A review of the statistical data driven approaches[J].European Journal of Operational Research,2011,213(1):1-14.

[5] FENG L,WANG H L,SI X S,et al.A state-space-based prognostic model for hidden and age-dependent nonlinear diffusion degradation process[J].IEEE Transactions on Automation Science and Engineering,2013,10(4):1072-1086.

[6] 彭寶華,周經倫,孫權.基于退化與壽命數據融合的產品剩余壽命預測[J].系統工程與電子技術,2011,33(5):1073-1078．

PENG B H,ZHOU J L,SUN Q.Residual lifetime prediction of products based on fusion of degradation data and lifetime data[J].Systems Engineering and Electronic,2011,33 (5):1073-1078(in Chinese).

[7] GEBRAEEL N Z,ELWANY A H,JING P.Residual life predictions in the absence of prior degradation knowledge[J].IEEE Transactions on Reliability,2009,58(1):106-117.

[8] SI X S,WANG W,HU C H,et al.Remaining useful life estimation based on nonlinear diffusion degradation process[J].IEEE Transactions on Reliability,2012,61(1):50-67.

[9] PENG W,LI Y F,YANGY J,et al.Inverse Gaussian process models for degradation analysis:A Bayesian perspective[J].Reliability Engineering & System Safety,2014,130(1):175-189.

[10] WANG W.A two-stage prognosis model in condition based maintenance[J].European Journal of Operational Research,2007,182(3):1177-1187.

[11] 王小林,程志君,郭波.基于維納過程金屬化模電容器的剩余壽命預測[J].國防科技大學學報,2011,33(4):146-151.

WANG X L,CHENG Z J,GUO B.Residual life forecasting of metallized film capacitor based on Wiener process[J].Journal of National University of Defense Technology,2011,33(4):146-151(in Chinese)．

[12] 王小林,郭波,程志君.融合多源信息的維納過程性能退化產品的可靠性評估[J].電子學報,2012,40(5):977-982．

WANG X L,GUO B,CHENG Z J.Reliability assessment of products with Wiener process degradation by fusing multiple information[J].Acta Electronica Sinica,2012,40(5):977-982(in Chinese)．

[13] WANG W,CARR M,XU W,et al.A model for residual life prediction based on Brownian motion with an adaptive drift[J].Microelectronic Reliability,2011,51(2):285-293.

[14] SI X S,WANG W,HU C H,et al.Estimating remaining useful life with three-source variability in degradation modelling[J].IEEE Transactions on Reliability,2014,63(1):167-190.

[15] WANG X.Wiener processes with random effects for degradation data[J].Journal of Multivariate Analysis,2010,101(2):340-351.

[16] PARK C,PADGETT W J.Accelerated degradation models for failure based on geometric Brownian motion and Gamma processes[J].Life Time Data Analysis,2005,11(4):511-527.

[17] GEBRAEEL N Z.Sensory-updated residual life distributions for components with exponential degradation patterns[J].IEEE Transactions on Automation Science and Engineering,2006,3(4):382-392.

[18] 司小勝,胡昌華,周東華.帶測量誤差的非線性退化過程建模與剩余壽估計[J].自動化學報,2013,39(5):530-541.

SI X S,HU C H,ZHOU D H.Nonlinear degradation process modeling and remaining useful life estimation subject to measurement error[J].Acta Automatica Sinica,2013,39(5):530- 541(in Chinese).

[19] 劉君強,謝吉偉,左洪福,等.基于隨機Wiener過程的航空發動機剩余壽命預測[J].航空學報,2015,36(2):564-574．

LIU J Q,XIE J W,ZUO H F,et al.Residual lifetime prediction for aeroengines based on Wiener process with random effects[J].Acta Aeronautica et Astronautica Sinica,2015,36(2):564-574(in Chinese)．

[20] 茆詩松,湯銀才.貝葉斯統計[M].北京:統計出版社,2012:10-16.

MAO S S,TANG Y C.The Bayesian statistics[M].Beijing:China Statistics Press,2012:10-16(in Chinese).