粒子群算法優(yōu)化的灰色神經(jīng)網(wǎng)絡(luò)衛(wèi)星鐘差預(yù)報
趙增鵬,楊 帆,張子文,張 磊
(遼寧工程技術(shù)大學(xué) 測繪與地理科學(xué)學(xué)院,遼寧 阜新 123000)
0 引言
衛(wèi)星鐘差預(yù)報在衛(wèi)星定位與導(dǎo)航中具有重要的作用。空間中的衛(wèi)星鐘很容易受到各種因素的影響[1],因此建立一種高精度的衛(wèi)星鐘差預(yù)報模型對提高鐘差產(chǎn)品質(zhì)量具有非常重要的意義。目前,鐘差預(yù)報常用的模型有多種[2-5],如二次多項式模型[6]、灰色模型[7-8],以及BP神經(jīng)網(wǎng)絡(luò)預(yù)報模型[9-10]等。其中,二次多項式模型具有物理意義明確、短期預(yù)報比較理想和計算簡單等優(yōu)點,但存在著預(yù)報誤差隨時間增長而不斷增大的不足[11-12];灰色模型需少量樣本即可建立模型,但是其預(yù)報精度可靠性不強[13];BP神經(jīng)網(wǎng)絡(luò)學(xué)習(xí)速度快、適用于非線性時序預(yù)報,但存在易陷入局部最優(yōu)、收斂速度慢等缺點。
為進一步提高衛(wèi)星鐘差預(yù)報精度,本文在灰色神經(jīng)網(wǎng)絡(luò)模型的基礎(chǔ)上采用粒子群優(yōu)化算法(particle swarm optimization,PSO)尋找模型的最優(yōu)參數(shù),建立粒子群優(yōu)化的灰色神經(jīng)網(wǎng)絡(luò)鐘差預(yù)報模型。
1 預(yù)報模型原理
1.1 灰色神經(jīng)網(wǎng)絡(luò)衛(wèi)星鐘差預(yù)報模型原理
根據(jù)灰色模型原理,首先對原始衛(wèi)星鐘差序列x(t)(t=0,1,2,…,N-1)進行一次累加,得到序列y(t),預(yù)測結(jié)果為z(t);將離散數(shù)據(jù)視為連續(xù)變量在其變化中所取的離散值,用微分方程式處理數(shù)據(jù),進行數(shù)據(jù)的擬合與預(yù)測。含有n個參數(shù)的灰色神經(jīng)網(wǎng)絡(luò)模型所對應(yīng)的微分方程式表示為
(1)
式中:y2,…,yn為系統(tǒng)輸入?yún)?shù);y1為系統(tǒng)輸出參數(shù);a,b1,b2,…,bn-1為微分方程系數(shù)。根據(jù)灰色神經(jīng)網(wǎng)絡(luò)原理,式(1)的時間響應(yīng)方程式可表示為
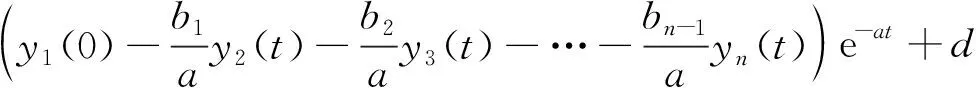
(2)
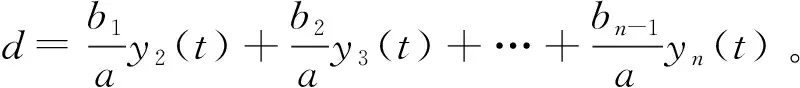
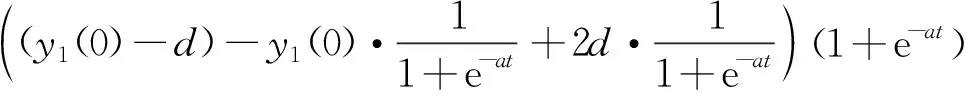
(3)
將式(3)映射到灰色神經(jīng)網(wǎng)絡(luò)中,可以得到含有n個輸入?yún)?shù)、1個輸出參數(shù)的灰色神經(jīng)網(wǎng)絡(luò),拓?fù)浣Y(jié)構(gòu)如圖1所示。
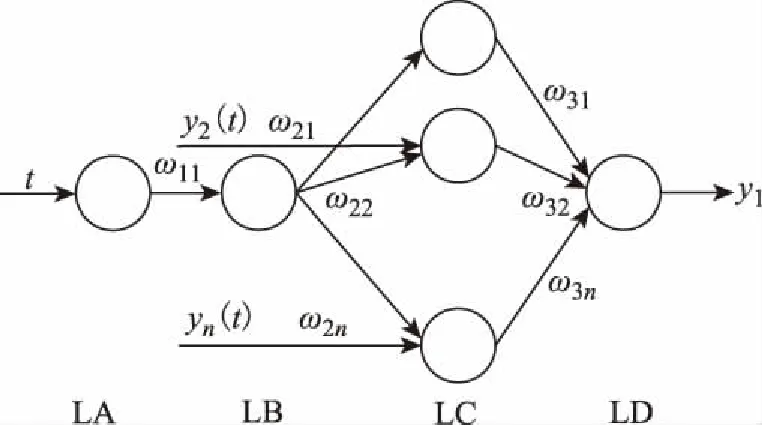
圖1 灰色神經(jīng)網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)
圖1中:t為輸入?yún)?shù)的序號;y2(t),…,yn(t)為網(wǎng)絡(luò)輸出參數(shù);ω21,ω22,…,ω2n,ω31,ω32,…,ω3n為網(wǎng)絡(luò)權(quán)值;y1為網(wǎng)絡(luò)預(yù)測值;LA、LB、LC、LD分別表示灰色神經(jīng)網(wǎng)絡(luò)的4層。
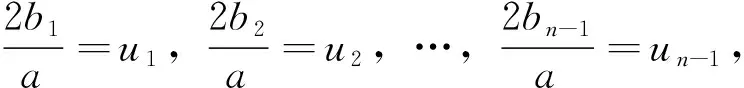
(4)
LD層中輸出節(jié)點的閾值表示為
θ=(1+e-at)(d-y1(0))
(5)
灰色神經(jīng)網(wǎng)絡(luò)的學(xué)習(xí)步驟如下:
1)根據(jù)所要進行訓(xùn)練的數(shù)據(jù)特征初始化參數(shù)a、b,并根據(jù)a、b的值計算出u的值。
2)根據(jù)網(wǎng)絡(luò)的權(quán)值計算ω11,ω21,ω22,…,ω2n,ω31,ω32,…,ω3n。
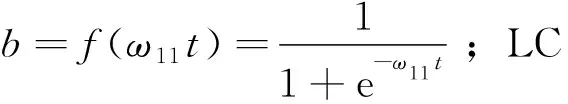
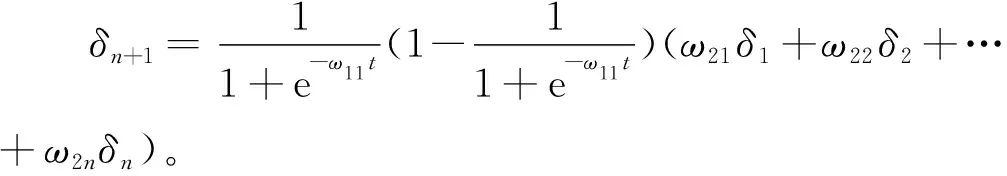
根據(jù)上述計算得到的預(yù)測誤差進一步調(diào)整權(quán)值:首先調(diào)整LB層到LC層的連接權(quán)值為ω21=-y1(0),ω22=ω22-μ1δ2b,…,ω2n=ω2n-μn-1δnb;然后調(diào)整LA層到LB層的連接權(quán)值為ω11=ω11+atδn+1;最后調(diào)整網(wǎng)絡(luò)閾值為
θ=(1+e-ω11t)
5)判斷訓(xùn)練是否結(jié)束,若否,返回步驟3)。
1.2 基于粒子群算法的灰色神經(jīng)網(wǎng)絡(luò)模型參數(shù)優(yōu)化
粒子群算法最早是由Eberhart和Kennedy在1995年研究鳥類捕食行為時提出的,是一種智能群體全局最優(yōu)化的算法[14]。PSO算法的原理是:在可解空間中隨機初始化粒子群,算法中的每個粒子都表示尋優(yōu)問題的一個潛在解,用速度、位置和適應(yīng)度值3個指標(biāo)來表示該粒子的特征,粒子的速度決定粒子在各移動方向上的距離,并且粒子的速度隨著自身和其他粒子的移動進行動態(tài)調(diào)整,從而實現(xiàn)個體在可解空間中的尋優(yōu);粒子的位置每更新一次,就計算一次粒子的適應(yīng)度值,并且根據(jù)個體極值、群體極值的適應(yīng)度值和新粒子的適應(yīng)度值進一步更新個體極值Pbest和群體極值Gbest的位置。PSO算法沒有交叉和變異等操作,算法收斂快、通用性強。采用粒子群算法優(yōu)化灰色神經(jīng)網(wǎng)絡(luò)的權(quán)值與閾值,不僅可以解決傳統(tǒng)灰色神經(jīng)網(wǎng)絡(luò)中隨機選取權(quán)值和閾值的弊端,而且還能加快網(wǎng)絡(luò)計算收斂的速度[15]。具體計算步驟如下:
1)將數(shù)據(jù)序列分為訓(xùn)練樣本與預(yù)測樣本。
2)應(yīng)用小波去噪理論對訓(xùn)練樣本進行降噪處理,在此基礎(chǔ)上應(yīng)用虛假鄰近法與互信息法求解最佳延遲時間與嵌入維數(shù),重構(gòu)高維數(shù)據(jù)序列。
3)參數(shù)的初始化:初始化粒子的速度及位置、權(quán)重系數(shù)及慣性權(quán)重,并且賦予初始粒子經(jīng)過的每個位置相應(yīng)的一組參數(shù),然后由設(shè)置的初始參數(shù)組合以及學(xué)習(xí)樣本建立灰色神經(jīng)網(wǎng)絡(luò)模型。
4)用預(yù)先設(shè)置的目標(biāo)函數(shù)來計算所有粒子的適度值。
5)將計算每個粒子得到的適度值與其對應(yīng)的最優(yōu)值進行比較分析,進一步判斷是否符合迭代的條件,若符合則此參數(shù)組合就是最優(yōu)參數(shù)組合,否則進行步驟6)。
6)根據(jù)速度與位置更新公式反復(fù)更新粒子的速度和位置,并判斷是否滿足最優(yōu)解,如果滿足則設(shè)置適應(yīng)度值的最小精度值或者達到最大的迭代次數(shù),若滿足條件就執(zhí)行步驟7)并輸出最優(yōu)的參數(shù),并重新對模型進行訓(xùn)練學(xué)習(xí),否則轉(zhuǎn)到步驟5)。
7)得到最優(yōu)參數(shù)組合。
1.3 預(yù)報模型建立
首先根據(jù)原始衛(wèi)星鐘差數(shù)據(jù)特征,采用粒子群算法尋優(yōu)灰色神經(jīng)網(wǎng)絡(luò)模型的最佳參數(shù)組合;然后將尋優(yōu)的最佳參數(shù)組合傳遞給灰色神經(jīng)網(wǎng)絡(luò)模型;最后進行鐘差預(yù)測。流程如圖2所示。
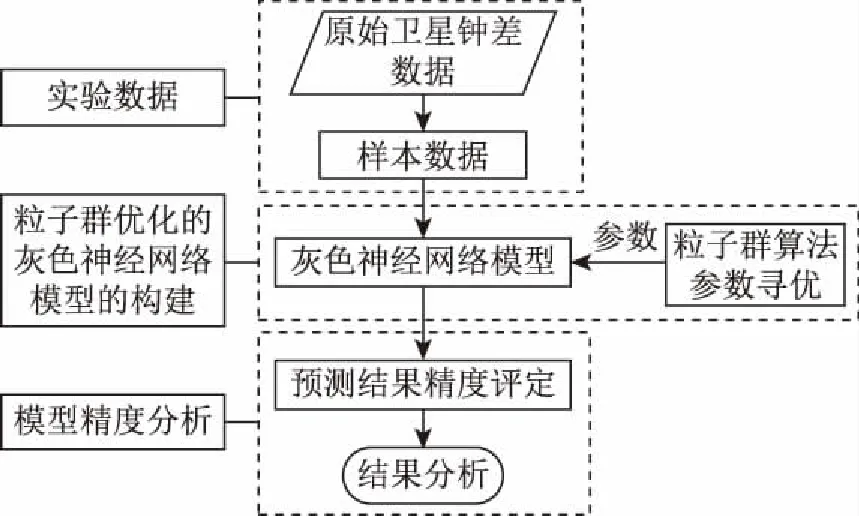
圖2 粒子群算法優(yōu)化的灰色神經(jīng)網(wǎng)絡(luò)模型
2 實驗與結(jié)果分析
為驗證算法的有效性與可行性,選用IGS提供的時間段為2014-02-22 T 00:00—23:55的精密鐘差產(chǎn)品。以編號為G06、G13、G14和G22 的4顆衛(wèi)星的精密鐘差數(shù)據(jù)為樣本,其采樣間隔為10 min,共計144組數(shù)據(jù)。將數(shù)據(jù)分為2組:前100期數(shù)據(jù)作為訓(xùn)練樣本以建立模型,剩下的44期數(shù)據(jù)作為檢測樣本以檢驗?zāi)P皖A(yù)測誤差。在MATLAB平臺下,分別采用灰色模型、灰色神經(jīng)網(wǎng)絡(luò)模型和本文方法進行對比分析。選取平均誤差(mean error,ME)與均方根誤差(root mean square error,RMSE)作為各個模型預(yù)報效果的評估標(biāo)準(zhǔn),其計算公式為
(6)
4顆衛(wèi)星第101~144期精密鐘差原始數(shù)據(jù)與3種預(yù)測模型的預(yù)測值對比情況如圖3所示。計算各預(yù)測模型預(yù)報誤差的結(jié)果如表1所示。

表1 3種模型衛(wèi)星鐘差預(yù)報誤差統(tǒng)計結(jié)果 ns
由圖3、表1分析可得以下結(jié)論:
1)由圖3可知,灰色模型與原始數(shù)據(jù)的偏離最大,預(yù)報精度最低;灰色神經(jīng)網(wǎng)絡(luò)次之;本文采用粒子群優(yōu)化的灰色神經(jīng)網(wǎng)絡(luò)預(yù)測模型與原始數(shù)據(jù)偏離最小,精度最高,是一種有效的鐘差預(yù)測模型。
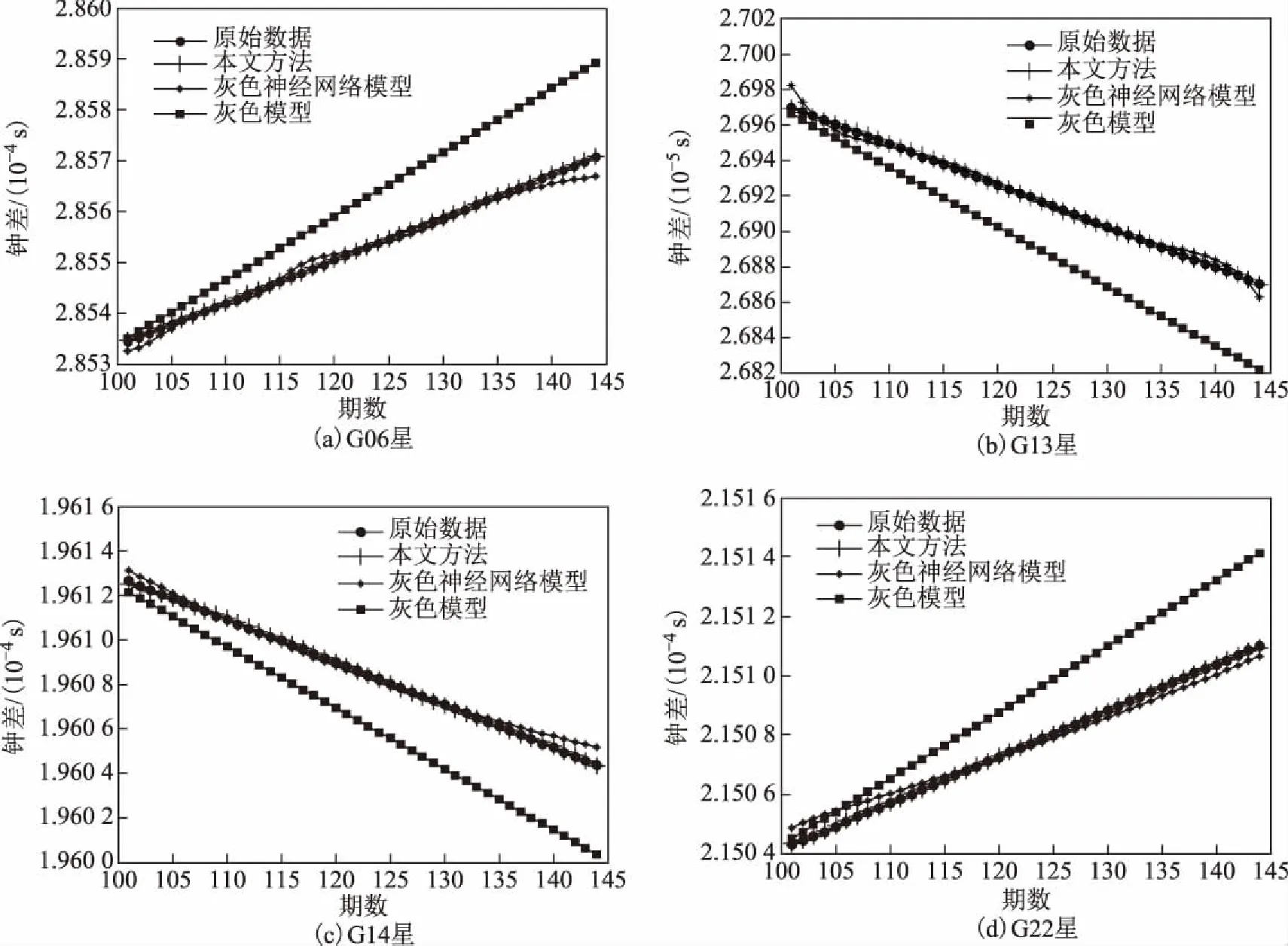
圖3 第101~144期原始鐘差與預(yù)報鐘差對比
2)由表1可知,無論原始衛(wèi)星鐘差是遞增還是遞減,本文算法的平均誤差與均方根誤差都是最小的,均小于0.1;而灰色模型與灰色神經(jīng)網(wǎng)絡(luò)模型誤差要大一個量級。
3)隨著預(yù)報期數(shù)的增加,3種模型的預(yù)報誤差也隨著增加;但是由于本文樣本數(shù)量相對較少,因此誤差累積不是很明顯。本文采用粒子群優(yōu)化的灰色神經(jīng)網(wǎng)絡(luò)預(yù)測模型得到的鐘差預(yù)測值可以很好地與原始鐘差數(shù)據(jù)吻合,證明了算法的可靠性與精度。
3 結(jié)束語
本文在研究粒子群算法、灰色神經(jīng)網(wǎng)絡(luò)的基礎(chǔ)上,提出把基于粒子群算法優(yōu)化的灰色神經(jīng)網(wǎng)絡(luò)模型用于衛(wèi)星鐘差預(yù)報,采用粒子群算法尋優(yōu)灰色神經(jīng)網(wǎng)絡(luò)所需的參數(shù),有效解決灰色神經(jīng)網(wǎng)絡(luò)參數(shù)選擇的隨機性與易陷入局部最優(yōu)的缺陷,進一步提高模型預(yù)報的精度。通過實例驗證,結(jié)果表明粒子群算法優(yōu)化的灰色神經(jīng)網(wǎng)絡(luò)精密鐘差預(yù)報模型穩(wěn)定性更強,能夠明顯提高衛(wèi)星鐘差的預(yù)報精度。
[1] HEO Y J,CHO J,HEO M B.Improving prediction accuracy of GPS satellite clocks with preriodic variation behaviour [J].Measurement Science and Technology,2010,21(7):110-118.
[2] 王宇譜,呂志平,陳正生,等.一種新的導(dǎo)航衛(wèi)星鐘差預(yù)報與內(nèi)插方法[J].大地測量與地球動力學(xué),2013,33(4):112-116.
[3] 王穎,徐波,楊旭海.一種利用泛函網(wǎng)絡(luò)進行導(dǎo)航衛(wèi)星鐘差預(yù)報的方法研究[J].宇航學(xué)報,2012,33(10):1401-1406.
[4] 黃觀文,楊元喜,張勤.開窗分類因子抗差自適應(yīng)序貫平差用于衛(wèi)星鐘差參數(shù)估計與預(yù)報[J].測繪學(xué)報,2011,40(1):15-21.
[5] 鄭作亞,黨亞民,盧秀山,等.附有周期項的預(yù)報模型及其在 GPS 衛(wèi)星鐘差預(yù)報中的應(yīng)用研究[J].天文學(xué)報,2010,51(1):95-102.
[6] 郭海榮.導(dǎo)航衛(wèi)星原子鐘時頻特征分析理論與方法研究[D].鄭州:信息工程大學(xué),2006.
[7] 鄭作亞,陳永奇,盧秀山.灰色模型修正及其在實時GPS衛(wèi)星鐘差預(yù)報中的應(yīng)用研究[J].天文學(xué)報,2008,49(3):306-320.
[8] 崔先強,焦文海.灰色系統(tǒng)模型在衛(wèi)星鐘差預(yù)報中的應(yīng)用[J].武漢大學(xué)學(xué)報(信息科學(xué)版),2005,30(5):447-450.
[9] 郭承軍,滕云龍.神經(jīng)網(wǎng)絡(luò)在衛(wèi)星鐘差短期預(yù)報中的應(yīng)用研究[J].測繪科學(xué),2011,36(4):198-200.
[10] 雷雨,趙丹寧.基于最小二乘支持向量機的鐘差預(yù)報[J].大地測量與地球動力學(xué),2013,33(2):91-95.
[11] 路曉峰,楊志強,賈曉林,等.灰色系統(tǒng)理論的優(yōu)化方法及其在衛(wèi)星鐘差預(yù)報中的應(yīng)用[J].武漢大學(xué)學(xué)報(信息科學(xué)版),2008,33(5):492-495.
[12] 王繼剛.基于GPS精密單點定位的時間比對與鐘差預(yù)報研究[D].北京:中國科學(xué)院研究生院,2010.
[13] YUAN Haibo,WANG Zhengming,DONG Shaoan,et al.Dynamic grey-autoregressive model of an atomic clock[J].Metrologia,2008,45(6):1-5.
[14] 楊瑩.基于支持向量機理論的露天邊坡沉降規(guī)律及預(yù)測研究[D].阜新:遼寧工程技術(shù)大學(xué),2014.
[15] GONSALVES T,ITOH K.GA optimization of Petri net-modeled concurrent service systems[J].Applied Soft Computing,2011,11(5):3929-3937.

