目標先驗知識未確知條件下MIMO雷達波形優化

雷曉艷 王洪雁

摘 要： 考慮雜波場景下改善MIMO雷達最差估計性能的穩健波形優化方法，根據最小最大方法，首先基于克拉美?羅界描述穩健波形優化問題。為求解所得復雜非線性問題，提出一種基于對角加載（DL）的迭代方法。此方法中，內層優化首先利用哈達瑪不等式被分解為若干個子問題。基于DL方法將子問題可以轉化為凸問題，外層優化同樣也可轉化為凸問題，因而此優化問題可獲得高效求解。初始優化問題的最優解可通過對迭代優化結果的最小二乘擬合得到。數值仿真驗證了所提方法的有效性。

關鍵詞： 多輸入多輸出雷達； 波形優化； 對角加載； 參數估計； 半定規劃； 最小二乘

中圖分類號： TN951?34 文獻標識碼： A 文章編號： 1004?373X（2018）11?0008?05

Waveform optimization of MIMO radar with imperfect target prior knowledge

LEI Xiaoyan1， WANG Hongyan2

（1. School of Network Engineering， Zhoukou Normal University， Zhoukou 466000， China；

2. School of Information Engineering， Dalian University， Dalian 116622， China）

Abstract： In this paper， the robust waveform optimization method to improve the worst?case estimation performance of multiple?input multiple?output （MIMO） radar in the clutter environment is considered. According to the min?max approach， the robust waveform optimization is described on the basis of Cramér?Rao bound （CRB）. In order to solve the complicated nonlinear problem， an iterative method based on diagonal loading （DL） is proposed. With the method， the inlayer optimization problem can be decomposed into some sub?problems first by means of the Hadamard inequation， and then these sub?problems are converted into the convex problem on the basis of DL method； the outer layer optimization problem can be also converted into the convex problem to get the effective solution of these optimization problems. The optimal solution of the original optimization problem can be obtained by means of the least squares （LS） fitting of the iterative optimization results. The efficiency of the proposed method was verified with numerical simulation.

Keywords： multiple?input multiple?output radar； waveform optimization； diagonal loading； parameter estimation； semidefinite programming； least square

0 引 言

受到多輸入多輸出（MIMO）技術在通信領域成功應用的啟發，MIMO概念最近被引入雷達領域，并受到越來越多的關注[1]。與傳統只發射相干波形的相控陣雷達不同的是，MIMO雷達幾乎可發射任意波形。根據陣元間距，MIMO雷達可分為分置雷達以及共置雷達。相比傳統的相控陣雷達，MIMO雷達幾乎可以發射任意波形，即所謂的波形分集[2]。因而，MIMO雷達比相控陣雷達具有更多的優勢，比如參數辨識性[2]，靈活的發射方向圖設計[3]。

波形設計是MIMO雷達研究領域中非常重要的方向之一。在目標及環境先驗知識確知條件下，文獻[4]研究了通過設計發射波形改善基于MIMO的空時自適應處理（STAP）方法的檢測性能[4]。文獻[5]基于某些準則，比如最小化克拉美?羅界（CRB）的跡等，設計波形以提高場景先驗知識完備場景下多個點目標的參數估計性能。文獻[6]則考慮了雜波場景下發射波形和接收權聯合優化以改善目標估計性能。顯然，求解上述文獻中波形設計問題需要某些參數的確切值，比如到達方向角（DOA）等。然而，這些參數在實際應用中須通過估計得到，因而不可避免存在誤差。因此，最終的參數估計性能相應地會受到這些參數估計誤差的影響，此現象已在文獻[5?6]中通過數值試驗驗證。

針對上述問題，基于最小化最差情況下（worst?case）CRB跡準則，通過將場景初始參數估計誤差凸集包含進波形優化，本文考慮了雜波場景下穩健波形優化問題以改善系統參數估計性能對參數初始估計誤差的穩健性。在發射功率及參數估計不確定凸集約束下，首先推導了穩健波形優化問題，為求解此復雜非線性問題，本文提出一種基于對角加載（DL）[7]的迭代方法。所提方法首先基于哈達瑪不等式（Hadamard′s Inequality）[8]將內層優化分解為多個獨立子問題，然后基于DL將子問題轉化為半定規劃問題（SDP）[9]，接著通過線性化方法將外層優化轉化為凸問題，進而此問題可獲得高效求解。最后，初始問題的最優解可通過對迭代所得結果的最小二乘（LS）擬合得到。

1 問題描述

考慮收發陣元數分別為[Mt]，[Mr]且具有任意陣元間距的共置窄帶MIMO雷達，其中第i個陣元發射的基帶信號為[?i∈CL×1， i=1，2，…，Mt]， [L]為采樣數，則所有基帶信號為[Φ=[?1，?2，…，?Mt]T]。基于上述模型，接收陣列所得信號可表示為：

[Y=k=1Kβka（θk）bT（θk）Φ+ΗcΦ+W] （1）

式中：[βkKk=1] 為目標幅度；[θkKk=1]則為[K]個目標待估計參數；[a（θk）=[ej2πf0τ1（θk），ej2πf0τ2（θk），…，ej2πf0τMr（θk）]T，b（θk）=][[ej2πf0τ1（θk），ej2πf0τ2（θk），…，ej2πf0τMt（θk）]T]分別表示位于[θk]的目標的接收及發射導向矢量， [f0]為載波頻率，[τm（θk）]為回波從位于[θk]的目標傳播至第m個接收陣元的時間， [τn（θk）]則表示信號從第n個發射陣元傳播至目標k的時間；[ΗcΦ]表示MIMO雷達接收的雜波信號，[Hc=i=1NCρ（θi）ac（θi）bTc（θi）]為雜波傳輸函數， [NC（NC?MtMr）]為感興趣距離環內雜波塊的數目， [ρ（θi）]為第i個雜波塊的反射系數，[ac（θi）]，[bc（θi）]分別表示位于[θi]雜波塊的接收發射導向矢量；[W]為干擾加噪聲項，類似于文獻[5]，其每一列可假設為服從零均值，方差矩陣為[P]且未知的獨立同分布循環對稱復高斯分布。

基于式（1），待估計參數[θ=[θ1，θ2，…，θK]T]及[βkKk=1]可表示如下（具體推導參見文獻[6]）：

[C=12Re（F11）Re（F12）-Im（F12）ReT（F12）Re（F22）-Im（F22）-ImT（F12）-ImT（F22）Re（F22）-1] （2）

式中：[Re?]，[Im?]分別為復數的實部及虛部。

[F11ij=β*iβjhHi（I+（RΦ?P-1）RHc）-1（RΦ?P-1）hj] （3）

[F12ij=β*ihHi（I+（RΦ?P-1）RHc）-1（RΦ?P-1）hj] （4）

[F22ij=hHi（I+（RΦ?P-1）RHc）-1（RΦ?P-1）hj] （5）

式中：[I]表示單位矩陣；[RΦ=Φ*ΦT]；[hk=b（θk）?a（θk）]；[hk=][?（b（θk）?a（θk））?θk， k=1，2，…，K；RHc=Evec（Hc）vecH（Hc）=][BcΞBHc?0]，其中，[E?]為期望算子，[vec?]為矢量算子，[Bc=b1，b2，…，bNC，bi=bc（θi）?ac（θi）， i=1，2，…，NC，Ξ=][diagσ21，σ22，…，σ2NC，] [σ2i=Eρ（θi）ρ*（θi）]。

由式（2）～式（5）可知，CRB為關于[θ]，[βkKk=1]，[Hc]的函數。實際應用中，這些參數須通過估計得到，因而不可避免存在誤差。因此，基于這些參數計算得到的CRB進行波形優化，會對初始參數估計誤差比較敏感，進而影響到系統參數估計性能，此現象已有文獻[5]中的數值試驗驗證。

本文只考慮目標先驗信息不確知條件下的穩健波形優化問題。設目標信道矩陣及微分可分別建模如下：

[hk=hk+δk， hk=hk+δk] （6）

式中：[hk，][hk]分別表示第[k]個目標信道矢量的真實值及其對應估計值；[hk，][hk]分別表示[hk]的微分真實值及其對應的估計值；[δk]為[hk]的估計誤差，其屬于凸集：[U1=δkδkF≤ζk，k=1，2，…，K ]，[δk]為[hk]的估計誤差，屬于凸集：[U2=δkδkF≤σk，k=1，2，…，K]。

基于以上討論，在發射功率及關于目標先驗知識不確知模型約束下，通過最小化最差情況下CRB以改善系統最差估計性能的穩健波形優化問題可表述如下：

[minRΦ maxδkKk=1， δkKk=1 tr（C）s.t. δk∈U1， δk∈U2 tr（RΦ）=LP， RΦ?0] （7）

由式（2）～式（6）知，優化問題為復雜的非線性問題，非常難以求解。

2 基于DL的迭代方法

為求解上述非線性優化問題，本文提出一種新的基于DL[7]的迭代方法。首先，考慮式（7）的內層優化。基于以下引理對內層優化進行簡化：

引理（哈達瑪不等式）[8]：假設[M]為[N×N]維半正定厄米特矩陣，則如下不等式：

[tr（M-1）≥i=1N1mii] （8）

成立，且等式成立當且只當[M]為對角陣。基于此引理，式（7）中內層優化可簡化為：

[maxδkKk=1， δkKk=1 k=1K12Re（F）kks.t. δk∈U1， δk∈U2] （9）

由式（2）～式（5）可知，式（9）可重寫為：

[maxδkKk=1， δkKk=1k=1K1β*khHkRtemphkβk+hHkRtemphks.t. δk∈U1， δk∈U2] （10）

式中：[Rtemp=（I+（RΦ?P-1）RHc）-1（RΦ?P-1）]，刪除[Re?]，是由于相加各項均為實數。

由式（10）可知，分母中第k項只依賴于[δk，][δk]。因此，優化問題式（10）可看做在對應約束下最大化每個相加項，換言之，此問題可分解為多個相互獨立的子問題：

[maxδkKk=1， δkKk=11β*khHkRtemphkβk+hHkRtemphks.t. δkF≤σk， δkF≤ζk， k=1，2，…，K] （11）

由于[P?0， RΦ?0， RHc?0，]則[（RΦ?P-1）RHc]為不定矩陣[8]，因此式（11）難以求解。為求解此問題，將DL方法應用于[RΦ]，則：

[RΦ=RΦ+εI?0] （12）

式中：[ε?λmax（RΦ）]為加載因子，[λmax（?）]取矩陣最大特征值。本文通過數值實驗選擇[ε=λmax（RΦ）1 000]。將式（11）中[RΦ]替換為[RΦ]，則可得[I+（RΦ?P-1）RHc-1]

[（RΦ?P-1）?0]。

明顯地，[β*khHk][（I+（RΦ?P-1）RHc）-1（RΦ?P-1）?][hkβk，] [hHk][（I+（RΦ?P-1）RHc）-1（RΦ?P-1）hk]分別為關于[δk，][δk]的凸函數[9]。此外，由式（11）可知，[δk]所屬凸集[δkKk=1]與[δk]所屬凸集[δkKk=1]相互獨立，則式（11）可以分解為如下兩個獨立優化問題：

[minδk β*khHkRtemphkβks.t. δkF≤σk] （13）

[minδk hHkRtemphks.t. δkF≤ζk] （14）

式中[Rtemp=（I+（RΦ?P-1）RHc）-1（RΦ?P-1）] 。

定理（Schur補）[8]：設[Z=ABHBC]為厄米特陣且[C?0，]則[Z?0]成立，當且僅當[ΔC?0，][ΔC=A-BHC-1B]為[Z ]Schur補。

基于上述定理，式（13），式（14）可分別轉化為如下SDP問題：

[mint，δk ts.t. σ2kδHkδkI?0tβ*khHkβkhkR-1Φ?P+RHc?0] （15）

[mint，δk ts.t. ζ2kδHkδkI?0thHkhkR-1Φ?P+RHc?0] （16）

式中[t]為輔助變量。將從式（15），式（16）得到的[δkKk=1]及[δkKk=1]代入式（7），考慮外層優化。

基于式（12），下述命題可將式（7）中關于[RΦ]的非線性問題線性化，且將相應約束轉化為線性矩陣不等式形式。

命題： 基于相關矩陣計算，式（7）中關于外層優化的約束可重新寫為如下形式：

[αI?D?βID=（I+（RΦ?P-1）RHc）-1（RΦ?P-1）] （17）

基于上述定理以及命題，類似于內層優化，外層優化可等價為如下SDP：

[minX，D tr（X）s.t. αI?D?βI， XIIF?0] （18）

式中[X]為輔助優化變量。

求解式（18）得到[D]后，[RΦ]可通過對LS擬合得到，即：

[RΦ=argminRΦ（D-1-RHc）-1-RΦ?P-1Fs.t. tr（RΦ）=LP RΦ?0 ] （19）

類似地，式（19）可等價為如下SDP：

[minRΦ， t ts.t. tvecH（Dtemp）vec（Dtemp）I?0 tr（RΦ）=LP， RΦ?0 ] （20）

式中：[Dtemp=（D-1-RHc）-1-RΦ?P-1。]式（15），式（16），式（18），式（20）可由文獻[10]的CVX工具箱高效求解。

基于以上討論，類似于文獻[11]中算法3，本文提出一種基于DL的迭代算法優化發射波形以最小化最差情況下CRB，從而改善MIMO雷達參數估計性能對目標參數估計誤差的穩健性，此算法描述如下：

算法：給定不確定凸集[U1，][U2]以及WCM的初始值，[RΦ]以及參數估計誤差可經過以下步驟迭代求得：

1） 求解式（15），式（16），得到最優[δkKk=1]及[δkKk=1]；

2） 求解式（18）得到[D]；

3） 重復以上步驟，直到最差情況下CRB變化不再明顯為止。

最后，[RΦ]可通過求解得到。

3 仿真結果及分析

本節通過將所提方法與非穩健方法[6]以及非相關波形對比以驗證所提方法有效性，此有效性可通過以下兩方面驗證：最差情況下參數估計性能的改善程度以及所提方法的穩健性。文中所用雷達發射接收陣元數皆為3，發射接收陣列相鄰陣元間距皆為半波長，記為MIMO雷達1，發射接收相鄰陣元間距分別為1.5，0.5倍波長，記為MIMO雷達2。雜波塊數[NC=10 000，]雜噪比（CNR）為30 dB。假設場景中存在具有單位幅度的目標位于[20°]，且干擾位于[-5°，]干噪比（JNR）為60 dB。此外，采樣數[L=256]。另外，如前所述，CRB的計算需要某些參數的估計值，這些參數估計值在應用中可由許多方法得到[12]。

本節假設僅目標角度估計存在誤差。假設初始角度估計誤差位于不確定集[Δθ=[-3°，3°]]，則初始角度估計為[θ=[17°，23°]]。經過計算，可得到MIMO雷達1場景下[ζ=5.438 2， σ=7.659 3]，MIMO雷達2場景下[ζ=][27.632 9]，[σ=29.675 4]。

首先所提方法可以得到陣列信噪比（ASNR，定義為[PMtMrσ2W]）為10 dB條件下最優發射波束方向圖，如圖1所示。由圖1可知，所提方法在目標所在位置周圍有最大增益，這說明雷達發射功率集中于關于參數估計誤差不確定集最差情況下CRB的位置，因而最差情況下參數估計精度可得到改善。此外，可以看到圖1b）中存在柵瓣，這是由于MIMO雷達2的稀疏發射陣列所致[5]。

為驗證最差情況下參數估計性能的改善程度，以目標角度確知條件下非穩健方法所得CRB為基準，所提方法以及非相關波形得到的最差情況下CRB隨ASNR的變化如圖2所示。明顯地，所得不確定凸集上最差情況下CRB皆隨ASNR增加而減小。并且，相比于非相關波形，所提方法可顯著降低最差情況下CRB，這是由于所提方法得到的波形將發射功率集中于凸不確定集，而非相關波形則全向發射。此外，可以看到，所提方法得到的CRB與基準CRB之間的差距比較小，這意味著所提方法可有效改善最差情況下參數估計性能。另外，比較圖2a）和圖2b），可知MIMO雷達2得到的最差情況下CRB要優于雷達1，這是由于前者形成的虛擬陣列長度大于后者[2]。

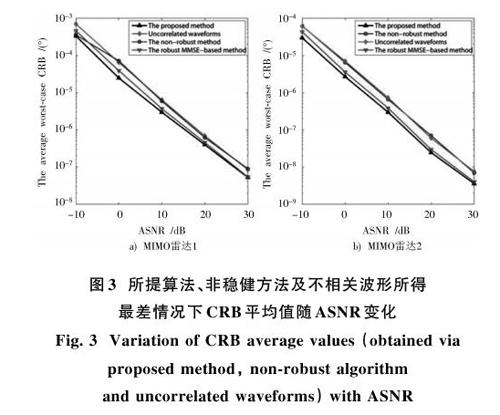
最后，為驗證所提算法的穩健性，所提算法、非穩健方法及不相關波形所得最差情況下CRB平均值隨ASNR變化如圖3所示。

由圖3可知，相比非穩健方法以及不相關波形，所提方法有最小的最差情況下CRB，換言之，所提方法相對于初始參數估計誤差有較好的穩健性。

4 結 論

在目標先驗知識非完備場景下，本文研究了雜波條件下穩健波形優化問題以改善共置MIMO雷達最差情況下參數估計性能。基于初始參數估計誤差模型以及發射功率約束，首先建立了穩健波形優化問題的表述。為求解所得復雜非線性優化問題，本文提出一種新的基于DL的迭代算法，此算法中每一次迭代都可轉化為SDP問題，因此可以獲得高效求解。初始問題的最優解可通過對迭代方法所得結果的LS擬合求得。數值仿真通過與非穩健方法以及非相關波形相比較，驗證了所提方法的有效性。

參考文獻

[1] TANG B， NAGHSH M M， TANG J. Relative entropy?based waveform design for MIMO radar detection in the presence of clutter and interference [J]. IEEE transactions on signal processing， 2015， 63（14）： 3783?3796.

[2] WANG H， LIAO G， LI J， et al. On parameter identifiability of MIMO radar with waveform diversity [J]. Signal processing， 2011， 91（8）： 2057?2063.

[3] CUI G， LI H， RANGASWAMY M. MIMO radar waveform design with constant modulus and similarity constraints [J]. IEEE transactions on signal processing， 2014， 62（2）： 343?353.

[4] WANG H， LIAO G， LI J， et al. Waveform optimization for MIMO?STAP to improve the detection performance [J]. Signal processing， 2011， 91（11）： 2690?2696.

[5] LI J， XU L， STOICA P， et al. Range compression and waveform optimization for MIMO radar： a Cramer?Rao bound based study [J]. IEEE transactions on signal processing， 2008， 56（1）： 218?232.

[6] WANG H， LIAO G， LIU H， et al. Joint optimization of MIMO radar waveform and biased estimator with prior information in the presence of clutter [J]. EURASIP journal on advances in signal processing， 2011， 15（1）： 1?13.

[7] HORN R A， JOHSON C R. Matrix analysis [M]. U.K.： Cambridge University Press， 1985.

[8] YU Z， GU Z， SER W， et al. Convex optimization and its applications in robust adaptive beamforming [C]// The 9th International Conference on Information， Communications and Signal Processing. Taiwan： China， 2013： 1?5.

[9] GRANT M， BOYD S. CVX： Matlab software for disciplined convex programming 2013 [EB/OL]. [2013?04?23]. http：//www.cvxr.com/cvx.

[10] ELDAR Y C， MERHAV N. A competitive minimax approach to robust estimation of random parameters [J]. IEEE transactions on signal processing， 2004， 52（7）： 1931?1946.

[11] WANG H， LIAO G， LI J， et al. Waveform optimization for MIMO radar based on Cramer?Rao bound in the presence of clutter [J]. IEICE transactions on communications， 2012， 95（6）： 2087?2094.

[12] XU L Z， LI J， STOPCA P. Adaptive techniques for MIMO radar [C]// The 4th IEEE Workshop on Sensor Array and Multi?Channel Processing. Waltham： IEEE， 2006： 258?262.