基于不平衡電網條件下的整流器預測直接功率控制

李坤奇 張斌 許偉奇 路小娟

摘 要： 電網不平衡時，傳統控制方法會加重網側諧波以及直流側電壓不穩定等問題。通過對PWM整流器建模分析，獲得靜止坐標系下的預測功率控制模型；使單位周期內的有功功率和無功功率等于給定的參考值，獲得控制電壓的矢量表達式，并推導出可以滿足不平衡電網條件下整流器控制要求的功率補償，從而實現不平衡條件下的整流器控制。該方法具有拓撲結構簡單，動態響應較快，能夠有效地實現網側電流正弦化，單位功率因數，穩定直流側電壓等優點，通過在Simulink環境下搭建其仿真模型充分驗證了該方法的正確性和有效性。

關鍵詞： 不平衡電網； PWM整流器； 預測功率控制； 直接功率控制； 功率補償； 擴展無功功率

中圖分類號： TN876?34 文獻標識碼： A 文章編號： 1004?373X（2018）11?0082?05

Predictive direct power control of rectifier under unbalanced grid condition

LI Kunqi， ZHANG Bin， XU Weiqi， LU Xiaojuan

（School of Automaton and Electrical Engineering， Lanzhou Jiaotong University， Lanzhou 730070， China）

Abstract： If the power grid becomes unbalanced， the traditional control methods may increase the grid?side harmonics and make the DC?side voltage instable. The PWM rectifier is modeled and analyzed to obtain the predictive power control model in the stationary coordinate system. It makes that the active power and reactive power within the unit period are equal to the given reference values to get the vector expression of the controlled voltage. The power compensation which satisfies the requirement of rectifier control under the unbalance grid condition is deduced to realize the rectifier control under unbalanced condition. This method has simple topology structure and fast dynamic response， and can realize the sinusoidal gird?side current effectively， unitize the power factor and stabilize the DC?side current. The correctness and effectiveness of the method are verified by means of simulation model built under Simulink environment.

Keywords： unbalanced grid； PWM rectifier； predictive power control； direct power control； power compensation； extended reactive power

0 引 言

隨著PWM整流器的廣泛應用，人們對其不平衡電網條件下的控制效果要求越高，近些年來不平衡電網下的控制策略被廣泛注意。文獻[1?2]通過消除負序電流實現直流側電壓的有效控制，該方法對于內部電流環的PI控制器參數的選取要求較高。文獻[3]提出擴展無功功率的計算，如此可以有效地表示不平衡電網下的無功功率，通過消除有功功率和無功功率的二倍頻波動，達到不平衡電網下的控制目的。但是正負序分量的提取會導致系統的穩定性降低以及動態響應速度較慢。

文獻[4?5]針對比例諧振控制器可以很好地實現正弦信號的無靜差跟蹤，提出不平衡電網下的直接功率控制，該方法基于兩相靜止坐標系下，無需進行正負序分解，在獲得網側正弦電流，以及消除功率的二倍頻波動上具有更好的效果，但是直接功率控制在信號采集頻率較低時不能獲得高品質的電流波形，且有頻率不固定的諧波問題。

針對上述問題，本文采用預測直接功率的控制方法，該方法是在預測控制原理的基礎上結合無差拍控制[6]的方法，對功率預測達到更好的控制功率效果。該方法相比傳統的直接功率控制具有簡單的控制結構，固定的開關頻率，更好的抗擾性。在此基礎上，根據文獻[7]提出的滿足不平衡電網下的控制電流，通過相應的計算可獲得滿足不平衡條件的復功率值，再減去理想條件下給定的功率參考值，可以得到不平衡電網下的功率補償，經過仿真驗證表明，該方法可以很好地實現不平衡電網下的整流器控制，具有理論指導意義。

1 不平衡電網下PWM整流器功率分析

三相電壓型整流器主電路結構見圖1。其中：[ea，eb，ec]為電網側三相電壓；[L]為網側電感；[R]為網側等效電阻；[Ua，Ub，Uc]為整流橋側控制電壓；[Udc]為負載側的直流電壓；[Sa，Sb，Sc]為每相開關狀態。

整流器在abc三相的數學模型為：

[LdiadtLdibdtLdicdt=-r000-r000-riaibic+ea-uaeb-ubec-uc] （1）

其中：

[uaubuc=23-13-13-1323-13-13-1323SaSbScUdc] （2）

通過[abcαβ]坐標變換，可以將上述表達式轉化成為兩相靜止[αβ]坐標系下的PWM整流器數學模型：

[eα=Riα+Ldiαdt+uαeβ=Riβ+Ldiβdt+uβ] （3）

瞬時功率理論[8]根據電流共軛與電壓乘積得到的復功率S，即：

[S=1.5i?e=p+jq] （4）

[p=Re（S）=1.5（i?e）q=Im（S）=1.5（i?e）] （5）

式中：“[?]”表示共軛；“[?]”和“[?]”分別表示矢量點積和叉積，但是這種無功功率的表示方法并不能很好地表現不平衡電網下的無功功率，所以有學者提出擴展無功功率，其中延遲量的求取，本文按照文獻[9]提出的基于帶通濾波器達到延遲90°的作用，不同于以往的延遲1/4周期法，該方法不能給系統引入時間延遲。

[q=e′αiα+e′βiβ] （6）

對靜止坐標系下的電壓電流及其相應的延遲量進行分析：

[eα=E1cos（ωt+φ1）eβ=E2cos（ωt+φ2），e′α=E1sin（ωt+φ1）e′β=E2sin（ωt+φ2）] （7）

[iα=I1cos（ωt+φ3）iβ=I2cos（ωt+φ4），i′α=I1sin（ωt+φ3）i′β=I2sin（ωt+φ4）] （8）

將式（7）和式（8）代入式（5），可以得出：

[p=34E1I1cos（φ1-φ3）+E2I2cos（φ2-φ4）+34E1I1cos（2ωt+φ1+φ3）+E2I2cos（2ωt+φ2+φ4）?p+p] 式中：[p]為有功功率的直流量；[p]為有功功率的震蕩量。可以表示為：

[p=34（eαiα+e′αi′α+eβiβ+e′βi′β）p=34k1cos（2ωt）+k2sin（2ωt）cos（2ωt）+34k2cos（2ωt）-k1sin（2ωt）sin（2ωt）] （10）

其中：

[k1=eαiα-e′αi′α+eβiβ-e′βi′βk2=eαi′α+e′αiα+eβi′β+e′βiβ] （11）

同理，將式（7），式（8）代入式（6），求得：

[q=34（e′αiα-eαi′α+eβiβ-eβi′β）q=34（e′αiα+eαi′α+e′βiβ+eβi′β）] （12）

2 預測功率控制

根據式（3）表示的平衡條件下有功功率和無功功率表達式，可以得出當采樣周期很小時，可以認為[e]在一個單位周期內不變化，則其有功功率和無功功率在一個周期內的變化可以表示為：

[p（k+1）-p（k）q（k+1）-q（k）=eα（k）eβ（k）eβ（k）-eα（k）?iα（k+1）-iα（k）iβ（k+1）-iβ（k）] （13）

根據式（3）轉化可得：

[Lddtiα（t）iβ（t）=eαeβ-uα（t）uβ（t）-Riα（t）iβ（t）] （14）

整流器的線電阻很小，可以忽略，所以可以得到單位時間內的電流變化值：

[iα（k+1）-iα（k）iβ（k+1）-iβ（k）=TLeα（k）eβ（k）-uα（k）uβ（k）] （15）

將式（15）代入式（13）中，可以得到：

[p（k+1）-p（k）q（k+1）-q（k）=TLeα（k）eβ（k）eβ（k）-eα（k）×eα（k）eβ（k）-uα（k）uβ（k）] （16）

則可以得到網側的控制電壓表達式為：

[uα（k）uβ（k）=eα（k）eβ（k）-LTeα（k）eβ（k）eβ（k）-eα（k）-1×p（k+1）-p（k）q（k+1）-q（k）] （17）

由于預測控制[10?11]的目的是使有功功率和擴展無功功率在下一周期等于其相應的參考值，則有：

[p（k+1）q（k+1）=p*（k+1）q*（k+1）] （18）

將式（18）代入式（17）中，得：

[uα（k）uβ（k）=eα（k）eβ（k）-LTeα（k）eβ（k）e′α（k）e′β（k）×p*（k+1）-p（k）q*（k+1）-q（k）] （19）

無功功率參考值計為零，有功功率參考值為直流側功率，當采樣周期很小時，可以假設相鄰兩個周期的有功功率變化值一致。

[p*（k+1）-p*（k）=p*（k）-p*（k-1）] （20）

可以得出：

[p*（k+1）q*（k+1）=2p*（k）-p*（k-1）q*（k）] （21）

將式（21）代入到式（19），基于預測功率得到了控制電壓表達式：

[uα（k）uβ（k）=eα（k）eβ（k）-LT（e2α（k）+e2β（k））×eα（k）eβ（k）eβ（k）-eα（k）Δp*（k）+εp（k）εq（k）] （22）

式中：[Δp*（k）]為跟蹤差值；[εp（k）]，[εq（k）]為實際有功功率和實際無功功率變化值。

3 功率補償部分

不平衡電網下的整流器有四條控制規則：一是穩定直流側功率；二是使無功功率為零，得到單位功率因數；三四是消除ps2和pc2，實現消除有功功率的波動。通過第一部分的功率分析，得出在不平衡電網下滿足上述四條控制規則的控制表達式：

[Pref000=34eαeβe′αe′βe′αe′β-eα-eβeαeβ-e′α-e′βe′αe′βeαeβiαiβi′αi′β] （23）

得出滿足條件的控制電流如下：

[i*=iαrefiβref=2Pref3DIPC-e′βe′α =2Pref3（eβe′α-eαe′β）-e′βe′α] （24）

以此為條件，通過[s*new=1.5i*e]，得出在不平衡電網條件下保持直流側功率穩定，功率因數惟一，有功功率波動為零的功率參考值。原有預測功率的功率參考值的有功功率部分為直流側有功功率，無功功率部分為零。通過：

[Scomp=Srefnew-Sref=1.5（iref*e）-（pref+jqref）] （25）

得到在原有基礎上滿足不平衡電網控制要求的功率補償值：

[pcompqcomp=0eαe′α+eβe′βeαe′β-eβe′αpref] （26）

4 仿真研究分析

為了驗證本文方法的有效性，在Simulink中建立如圖2所示的仿真模型。為了進行有效的比較，三種方法采用的參數一致，具體參數選取如表1所示。

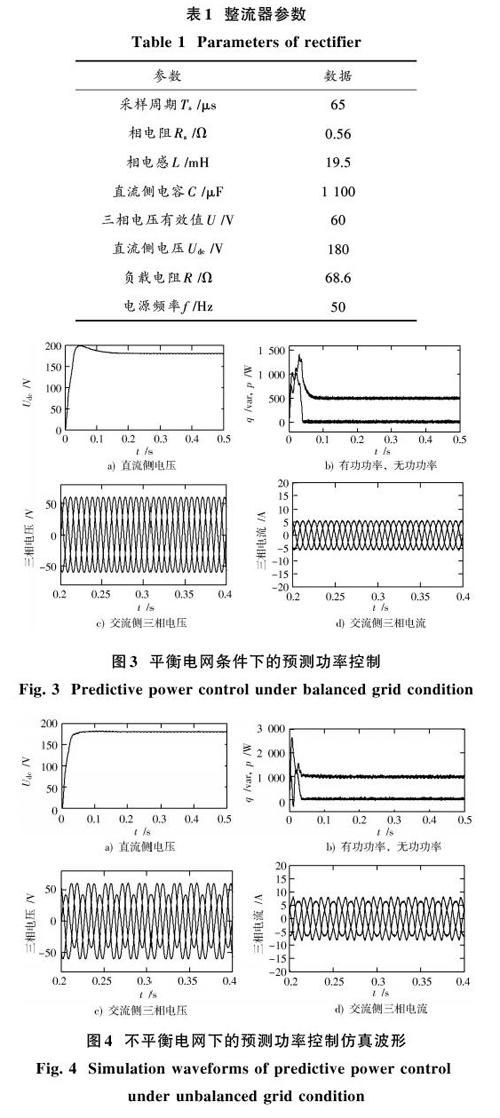
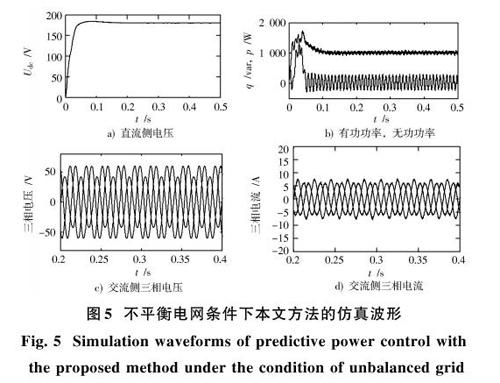
本文分別驗證了預測控制技術在平衡電網條件下的仿真結果，不平衡電網下的仿真結果，不平衡條件下的預測加補償的仿真結果。本文采用電壓跌落的方法實現不平衡電網的設定，a相電壓跌落30%，其余兩相位正常。為了有效驗證本文方法的正確性，本文分別進行了三個方面的實驗驗證，圖3為平衡電網條件下的整流器預測功率研究，圖4為不平衡電網條件下的整流器預測功率研究，圖5為不平衡電網條件下的預測功率加功率補償后的研究。其中，圖a）～圖d）分別為直流側電壓波形、有功功率和無功功率波形、三相電壓波形以及三相電流波形。

圖3為理想電網條件下的預測功率控制，可以看出，在理想電網條件下采用這一預測控制可以實現穩定直流側電壓，有功功率恒定，無功功率為零，且交流側電流正弦化。圖4為不平衡電網條件下的仿真圖，仿真結果表明，在不平衡條件下，直流側電壓發生波動，通過Powergui中的FFT工具箱得出交流側諧波發生畸變THD為23.5%，直流側電壓發生振蕩。圖5為加入功率補償之后的結果，直流側電壓趨于平穩，加入功率補償后，有功功率不變，無功功率發生振蕩，但平均無功功率為零，功率因數仍為1，交流側諧波THD為4.3%，說明交流側電流諧波也得到很好的抑制。仿真結果表明，不平衡電網條件下的預測控制加入功率補償后具有良好的控制效果。

5 結 論

本文采用一種新型預測功率控制，該方法具有固定的開關頻率，結構簡單，快速的響應能力，在此基礎上推導出滿足不平衡電網條件下的功率補償值，通過與預測控制在不平衡電網下的仿真對比，可以看出，加入功率補償后的預測控制可以很好地消除不平衡電網下網側電流諧波，實現單位功率因數，以及穩定直流側電壓，通過在Simulink上搭建的仿真模型，充分驗證了該方法的正確性和有效性。

參考文獻

[1] RIOUAL P， POULIQUEN H， LOUIS J P. Regulation of a PWM rectifier in the unbalanced network state using a generalized model [J]. IEEE transactions on power electronics， 1996， 11（3）： 495?502.

[2] 鄭征，王聰，葛廣凱.電網不平衡條件下PWM整流器正負序分量新計算方法[J].武漢大學學報（工學版），2010，43（5）：642?645.

ZHENG Zheng， WANG Cong， GE Guangkai. A new calculation algorithm of positive and negative sequence component of a PWM converter under voltage unbalance condition [J]. Journal of Wuhan University （engineering）， 2010， 43（5）： 642?645.

[3] HU J， HE Y. Modeling and control of grid?connected voltage?sourced converters under generalized unbalanced operation conditions [J]. IEEE transactions on energy conversion， 2008， 23（3）： 903?913.

[4] 年珩，程鵬.電網電壓不平衡時PWM整流器的諧振直接功率控制策略[J].電工技術學報，2013，28（11）：86?94.

NIAN H， CHENG P. Resonant based direct power control strategy for PWM rectifier under unbalanced grid voltage condition [J]. Transactions of China electrotechnical society， 2013， 28（11）： 86?94.

[5] ZHANG Y， QU C. Direct power control of a pulse width modulation rectifier using space vector modulation under unbalanced grid voltages [J]. IEEE transactions on power electronics， 2015， 30（10）： 5892?5901.

[6] 高吉磊，黃先進，林飛，等.基于重復觀測器的PWM整流器無差拍控制[J].電工技術學報，2010，25（6）：47?54.

GAO Jilei， HUANG Xianjin， LIN Fei， et al. Deadbeat control strategy for PWM rectifiers based on repetitive observer [J]. Transactions of China electrotechnical society， 2010， 25（6）： 47?54.

[7] LI Z， LI Y， WANG P， et al. Control of three?phase boost?type PWM rectifier in stationary frame under unbalanced input voltage [J]. IEEE transactions on power electronics， 2010， 25（10）： 2521?2530..

[8] AKAGI H， KANAZAWA Y， NABAE A. Instantaneous reactive power compensators comprising switching devices without energy storage components [J]. IEEE transactions on industry applications， 2008， 20（3）： 625?630.

[9] 宋文祥，董英，阮智勇.電網電壓不平衡時三電平整流器靜止坐標系控制研究[J].電網技術，2013，37（1）：94?99.

SONG Wenxiang， DONG Ying， RUAN Zhiyong. Control of three?level rectifier in stationary coordinate system under unbalanced grid voltage [J]. Power system technology， 2013， 37（1）： 94?99.

[10] WANG F， LI S， MEI X， et al. Model?based predictive direct control strategies for electrical drives： an experimental evaluation of PTC and PCC methods [J]. IEEE transactions on industrial informatics， 2015， 11（3）： 671?681.

[11] ZHANG Zhiwen， LI Song， XIE Xiaocheng， et al. Research on predictive power control of three?phase voltage source PWM rectifier [J]. Journal of power supply， 2017， 15（5）： 123?130.

[12] SUH Y， LIPO T A. Modeling and analysis of instantaneous active and reactive power for PWM AC/DC converter under generalized unbalanced network [J]. IEEE transactions on power delivery， 2006， 21（3）： 1530?1540.