基于蜻蜓算法的PID控制器參數優化
李小魁 黃全振 黃明明
摘 要: 為了解決傳統PID參數優化方法易出現費時、震蕩且不能保證所調參數最優的問題,提出一種基于蜻蜓算法的PID控制參數優化方法,該方法利用蜻蜓群體尋找食物的過程并以誤差性能指標ITAE作為其適應度函數實現PID控制參數的優化。通過仿真實驗,并與粒子群優化算法、人工蜂群算法、布谷鳥搜索算法等常用的PID參數整定方法進行比較,結果表明,基于蜻蜓算法優化的PID控制器具有更優的控制性能。
關鍵詞: 蜻蜓算法; PID控制器; 參數優化; ITAE; 控制性能; 反饋控制策略
中圖分類號: TN876?34; TP18 文獻標識碼: A 文章編號: 1004?373X(2018)12?0102?06
Abstract: To solve the problems of time?consuming, vibration, and inability to guarantee the adjusted parameters optimal in the traditional PID parameter optimization method, a PID control parameter optimization method based on dragonfly algorithm is proposed. In the method, the PID control parameters are optimized by using the process of dragonfly population searching for food and taking the error performance indicator ITAE as the fitness function. The simulation experiment results show that, in comparison with the common PID parameter tuning methods such as particle swarm optimization algorithm, artificial bee colony algorithm, and cuckoo search algorithm, the PID controller based on dragonfly algorithm optimization has a better control performance.
Keywords: dragonfly algorithm; PID controller; parameter optimization; ITAE; control performance; feedback control strategy
0 引 言
PID控制器是最早提出的反饋控制器之一[1],在工業控制領域,有超過95%的反饋回路部件使用的是PID控制器,然而由于PID控制本質是一種線性控制規律,在實際工業應用中對于一些非線性、高階、時滯的復雜系統,常規的PID控制效果并不能滿足生產要求。因此,PID控制器的參數優化一直是控制理論研究的一個重要課題。
蜻蜓算法(Dragonfly Algorithm,DA)[2]源于自然界中蜻蜓捕食、遷徙和躲避外敵的群體行為,實現對目標函數的優化。該算法不僅具有粒子群算法的個人認知和社會認知能力,同時結合了布谷鳥算法[3]中[Le′vy]飛行行為,在算法尋優過程中能夠有效避免陷入局部最優,提高算法的搜索性能。本文將蜻蜓算法用于PID控制器參數優化,基本思路是將PID控制器待優化的參數作為蜻蜓個體的位置信息,并以誤差性能指標ITAE作為其適應度函數,利用蜻蜓群體尋找食物的過程實現對PID控制參數的優化。并選取7類工業控制中的典型控制模型,通過Matlab對各系統進行仿真實驗,并與粒子群算法[4?6]、人工蜂群算法、布谷鳥搜索算法等幾種常用的PID參數優化方法進行比較。實驗結果表明,利用蜻蜓算法優化的PID控制器對各控制模型均具有很好的控制性能。

1 PID控制器
PID控制器的規律為:
4.3.2 20次獨立運行整定結果對比
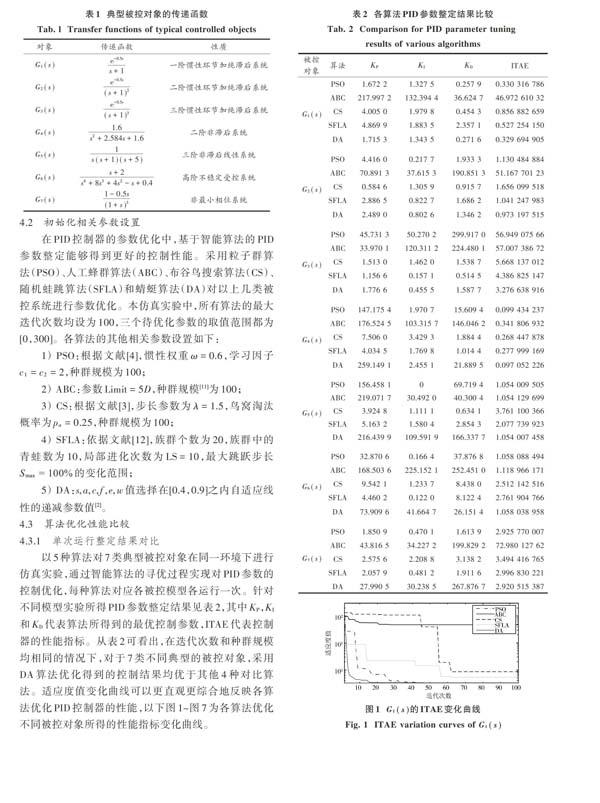
考慮到智能優化算法的隨機性,在上述相同的環境下,各算法針對7類不同控制模型分別進行20次獨立仿真實驗,從整定得到的ITAE性能指標結果的最優值、最差值、平均值和方差進行不同的算法分析,結果見表3。從表3可看出,對于[G1(s)],[G3(s)]和[G5(s)]被控對象,蜻蜓算法在最優值、最差值、平均值和方差的仿真結果均優于其他4種算法;對于[G2(s)],[G4(s)]和[G6(s)]這三個被控對象,蜻蜓算法的最優值、最差值、平均值均優于其他對比算法;而對于[G7(s)]非最小相位系統,蜻蜓算法的最優值略差于粒子群算法,但其在最差值、平均值和方差方面均優于粒子群算法和其他對比算法。綜合表2和表3中數據及圖1~圖7中性能指標進化曲線的對比分析,從性能指標、響應時間及適用的廣泛性等角度來考慮,對于7類不同典型被控系統,本文算法明顯優于其他4種算法。

5 結 語
針對傳統PID整定方法過程中可移植性差、費時且不能保證最佳控制性能的不足,提出一種基于蜻蜓算法優化的PID控制器。利用蜻蜓算法的尋優能力強的特點,將蜻蜓的位置定義為PID控制器的三個參數,將蜻蜓群體尋找獵物的過程視為實現PID控制參數的優化。在Simulink環境下,PID控制系統模型的每組控制參數對應的ITAE性能指標值得到最優的控制參數對被控系統進行控制,具有較強的自適應性和魯棒性。本文選取工業控制中常見的7類被控系統進行仿真實驗,實驗結果表明,基于蜻蜓算法的PID控制器具有更好的控制性能和魯棒性,因此,在工業控制中有較好的應用前景。
注:本文通訊作者為黃全振。
參考文獻
[1] ABACHIZADEH M, YAZDI M R H, YOUSEFI?KOMA A. Optimal tuning of PID controllers using artificial bee colony algorithm [C]// Proceedings of IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Montreal: IEEE, 2010: 379?384.
[2] MIRJALILI S. Dragonfly algorithm: a new meta?heuristic optimization technique for solving single?objective, discrete, and multi?objective problems [J]. Neural computing & applications, 2016, 27(4): 1053?1073.
[3] 王慶喜,儲澤楠.基于動態布谷鳥搜索算法的PID控制器參數優化[J].計算機測量與控制,2015,23(4):1215?1217.
WANG Qingxi, CHU Zenan. Parameters optimization of PID controller based on dynamic cuckoo search algorithm [J]. Computer measurement & control, 2015, 23(4): 1215?1217.
[4] 楊智,陳志堂,范正平,等.基于改進粒子群優化算法的PID控制器整定[J].控制理論與應用,2010,27(10):1345?1352.
YANG Zhi, CHEN Zhitang, FAN Zhengping, et al. Tuning of PID controller based on improved particle?swarm?optimization [J]. Control theory & applications, 2010, 27(10): 1345?1352.
[5] 胡偉,徐福緣.基于改進粒子群算法的PID控制器參數自整定[J].計算機應用研究,2012,29(5):1791?1794.
HU Wei, XU Fuyuan. Self?tuning of PID parameters based on improved particle swarm optimization [J]. Application research of computers, 2012, 29(5): 1791?1794.
[6] 熊偉麗,徐保國,周其明.基于改進粒子群算法的PID參數優化方法研究[J].計算機工程,2005,31(24):41?43.
XIONG Weili, XU Baoguo, ZHOU Qiming. Study on Optimization of PID parameter based on improved PSO [J]. Computer engineering, 2005, 31(24): 41?43.
[7] 鄭坤明,張秋菊.基于彈性動力學模型與遺傳算法的Delta機器人模糊PID控制[J].計算機集成制造系統,2016,22(7):1707?1716.
ZHENG Kunming, ZHANG Qiuju. Fuzzy PID control of delta robot based on elastic dynamic model and genetic algorithm [J]. Computer integrated manufacturing systems, 2016, 22(7): 1707?1716.
[8] WIKELSKI M, MOSKOWITZ D, ADELMAN J S, et al. Simple rules guide dragonfly migration [J]. Biology letters, 2006, 2(3): 325?329.
[9] 李遠梅,張宏立.基于改進螢火蟲算法PID控制器參數優化研究[J].計算機仿真,2015,32(9):356?359.
LI Yuanmei, ZHANG Hongli. Optimization of PID controller parameters based on improved glowworm swarm algorithm [J]. Computer simulation, 2015, 32(9): 356?359.
[10] 曾成,趙錫均.改進量子遺傳算法在PID參數整定中應用[J].電力自動化設備,2009,29(10):125?127.
ZENG Cheng, ZHAO Xijun. Application of improved quantum genetic algorithm in PID parameter tuning [J]. Electric power automation equipment, 2009, 29(10): 125?127.
[11] 蔡超,周武能.人工蜂群算法整定PID控制器參數[J].自動化儀表,2015,36(8):74?77.
CAI Chao, ZHOU Wuneng. Self?tuning PID parameters by using artificial bee colony algorithm [J]. Process automation instrumentation, 2015, 36(8): 74?77.
[12] HUYNH T H. A modified shuffled frog leaping algorithm for optimal tuning of multivariable PID controllers [C]// Proceedings of IEEE International Conference on Industrial Technology. Chengdu: IEEE, 2008: 1?6.

