基于干擾模型的機群保障點失效應急重構策略生成方法

趙坤朋，劉權利

(中國直升機設計研究所，江西 景德鎮 333001)

0 引言

艦載直升機的研制，除了需要考慮直升機各系統功能性能的滿足，還需要考慮直升機與艦船的適配性問題[1]。由于艦、機研制流程不同，研制思路不同，研制周期不同，研制顆粒度不同，導致艦船、直升機在均能滿足各自設計要求的條件下，仍不能有效配合，達不到理想的作戰效果。艦機適配性設計的目標是通過設計，提出各階段工作要求以及試驗驗證，實現艦與艦載機之間的相互適應和正確配合，實現艦上資源合理、有效的應用，確保艦載機上艦安全使用與維護，使航空聯隊的作戰效能得以發揮。艦機適配性設計包括艦機技術協調、直升機適配性設計、維修及任務支援系統研制三部分。維修及任務支援系統研制是根據艦載直升機的特殊使用方式，從陸艦保障一體化、通用化、集成化的角度出發，規劃、研制直升機艦基使用、維護及訓練支援保障所需的各類資源，為艦上機務部門實施保障提供各類工具、設備及信息化的作業支持環境，實現空地勤人員隨艦任務期間技術保持所必需的訓練需求，構建艦載直升機艦基保障系統和訓練保障系統，確保艦載直升機作戰效能的發揮[2]。

本文研究艦載直升機機群的使用保障與維修保障過程中，艦船甲板空間大小的限制、備件數量的限制、機務人員不足等原因，均會導致直升機不能得到及時的保障，從而影響其戰備完好率，進而影響艦載直升機的作戰效能[3]。為簡化實際工作中復雜的保障任務，本文將上述因素均抽象為艦船上保障點不可用，研究如何在保障點不可用的情況下，通過調整原來的保障方案實現機群出動架次率的最大化，從而保證作戰任務的完成。針對保障點失效擾動，建立了考慮保障任務成功率和偏離成本的干擾模型，并利用拉格朗日松弛法和次梯度優化算法給出了一組目標函數值；根據模型求解過程中的啟發式信息，提出一種啟發式算法[4]求出問題的可行解。最后，利用艦載直升機機群保障任務案例驗證方法的有效性。

1 問題描述

1.1 基本假設

為了對直升機機群保障過程中保障點失效擾動的影響進行分析，并得出一個較優的調整方案，本文做出以下假設：

假設1：只考慮保障點失效擾動；

假設2：直升機完成保障任務的時間以及失效保障點恢復時間均已知；

假設3：直升機的保障工作可恢復，指當某直升機正在保障時，其所在的保障點失效，則該直升機不必重新開始保障，其后續保障時間等于該直升機總保障時間減去已保障時間；

假設4：直升機可在不同保障點之間運輸，需考慮直升機在不同保障站點之間運輸的時間。

1.2 機群保障應對保障點失效過程

在機群保障過程中，保障點失效擾動是隨時發生的。在保障資源有限的情況下，該擾動的發生將會導致機群保障時間和保障費用的增加[5]。為了對保障點失效擾動下機群保障方案的調整過程進行分析，本文給出了基于干擾模型的機群應急重構策略生成方法的研究框架，如圖1，并將機群應對保障點失效這一特定擾動的過程簡化為以下步驟：

圖1 機群保障點失效的應急重構方法框架

步驟1：判斷保障點狀態，將保障點發生失效的時刻設為時刻0，并對失效保障點編號為1；

步驟2：更新保障點失效時刻正在進行保障任務的直升機的保障時間；

步驟3：直升機重新選擇保障點，更新直升機在保障點中的順序，形成應對擾動的優化方案；

步驟4：若在擾動未結束或者結束時再次發生保障點失效，即發生了新的擾動，則重復步驟1、2和3，并在上次優化方案的基礎上形成新的優化方案；

步驟5：以此類推，直到機群中所有直升機完成保障任務。

1.3 參數和變量定義

在保障點失效擾動下，機群保障方案的調整過程要考慮兩個方面的約束指標：①保障任務成功率。順利完成機群保障任務是機群執行出動任務的前提。②保障偏離成本。直升機要根據決策需求重新選擇保障點進行保障，并由此引發保障時間和保障順序發生變化，進而導致保障成本的增加。

在對機群保障過程中保障點失效擾動建立干擾模型之前，首先對模型需求的參數進行說明，如表1所示。

表1 干擾模型參數

直升機單元在保障過程中某個時刻的保障作業情況用0-1整數變量表示：

i=1，2，…，n；j=1，2，…，m；t=1，2，…，T

注：上述第二個變量中的“1”表示1個時間單位。

2 干擾模型

機群保障過程中保障點失效擾動將產生保障方案調整的需求，在該過程中要確保保障任務成功率的最大化和偏離成本的最小化。

1)保障任務成功率。為使目標函數為最小化的形式，本文從反面角度來衡量保障方案的優劣，用風險程度(保障任務成功率的對立面)來衡量方案的優劣，將風險定義為在任務規定時間內，沒有完成保障作業的直升機架數與要求出動的直升機架數的比值。

2)偏離成本。在機群出動任務過程中的偏離成本來源于兩方面：①直升機開始保障時間的偏離。保障點失效導致直升機初始開始保障時間的改變，并由此產生對相應保障設備、資源的規劃影響。②保障費用的偏離，這里指由于保障策略的不同而額外增加的費用，如直升機在不同保障點之間的運輸費用。

3)模型建立。根據以上內容建立機群保障過程中保障點失效的干擾模型，簡稱原問題IP:

(2.1)

subject to

(1)

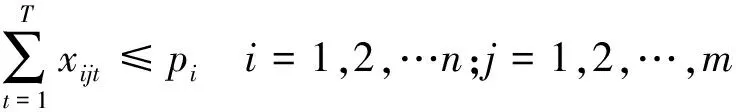
(2)

Bi1≥Di≤n

(3)

Bij≥tTifj≠1 andZi=1

(4)

α+β+γ=1

(5)

xijt∈{0,1}i=1,2,…n;t=1,2,…,T

(6)

(2.2)

在目標函數(2.1)中，α，β和γ分別是保障作業風險程度、開始保障時間偏離量和出動費用偏離量的權重。約束(1)保證在任何時間段t都至多有Mt個直升機在進行保障；約束(2)保證每架直升機在時間段T內的總保障時間小于其要求的保障時間；約束(3)表明只有當失效保障點可用后才能開始新的保障工作；約束(4)反映與原方案相比在新保障點完成保障作業的直升機，只有當調度到新保障點之后才能開始保障；約束(5)表明保障作業任務成功率和偏離成本權重之間的關系；約束(6)定義了變量范圍。

3 算法設計

3.1 Lagrange松弛及其對偶問題

對IP中的保障站點數量約束進行松弛，令λ=(λ1,λ2,…,λT)T,λ≥0為松弛約束的拉格朗日乘子，則ZIP對λ的Lagrange松弛為：

(3.1)

subject toλ=(λ1,λ2,…,λT)T≥0and(2)～(6)

式(3.1)中，對于任意給定的λ≥0，zLR(λ)≤zIP成立，zLR(λ)是zIP的下界，我們的目的是求與zIP最接近的下界，于是需要求解IP問題的拉格朗日對偶LD，如式(3.2)所示：

(3.2)

subject to(2)～(6)

3.2 對偶問題求解

λh+1=λh+θhg(λh)

(3.3)

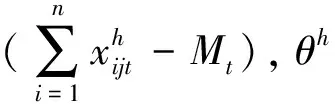
(3.4)

當下述兩個條件中的任何一個滿足時，則迭代停止：

2)λh或zLR(λh)在規定的步數內變化不超過給定的值，則認為目標值不可能再變化，停止運算。

3.3 構造一個可行的方案

4 案例研究

假設一個機群共有20架同型直升機，8個保障點，出動模式為最大出動模式，即要求20架直升機一次性出動。在出動過程中，只考慮保障點失效情況，假設直升機不發生故障。設定直升機保障作業過程中保障點失效時刻為時刻0，3號保障點故障。因為一批直升機已經保障一段時間了，因此這批直升機的保障時間要小于另一批直升機的保障時間。直升機按保障時間從小到大編號，即保障時間最短的直升機序號為1，以此類推。各參數為：D=30,tT=20,T=100,α=0.5,β=0.3,γ=0.2。表2為各直升機的保障時間及在原來方案和調整方案中的開始保障時間。表3為初始方案和調整方案中各直升機在保障點上的保障順序。

表2 初始數據

表3 初始方案與恢復方案中各個保障點上直升機保障次序

由表3知，只有直升機3、11、12的出動安排與原計劃不同，即調整方案與初始方案之間的偏離很小，并且調整方案能保證在規定的時間內出動任務要求的直升機架數，初始保障方案及新保障方案中的直升機保障順序如圖2、圖3所示。

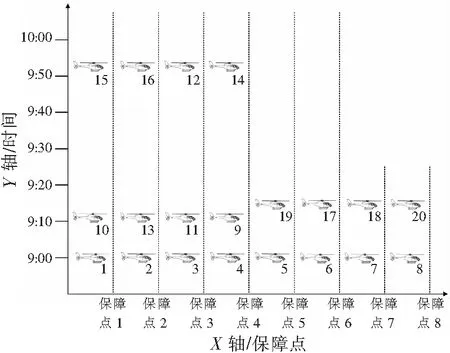
圖2 初始保障方案中直升機的保障順序

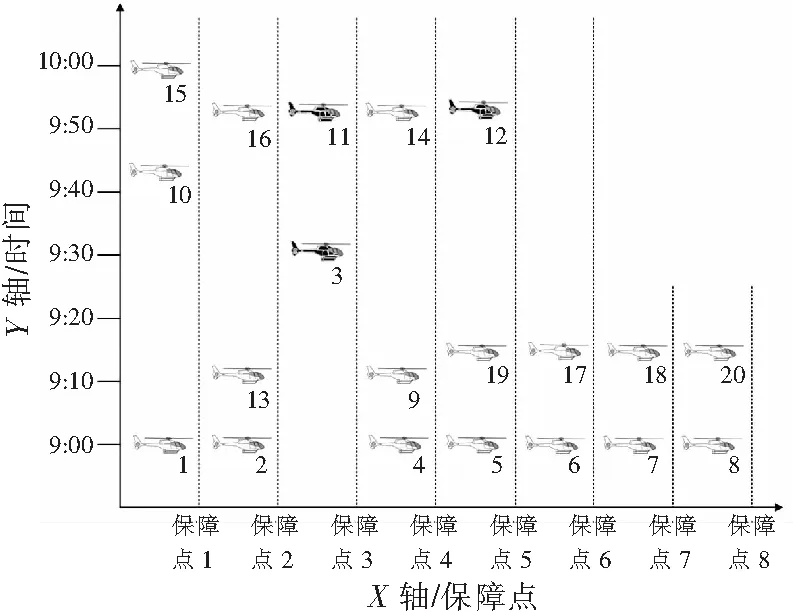
圖3 新保障方案中直升機的保障順序

5 結論

本文針對艦機適配性設計中的航空保障系統對艦載機群進行使用保障和維修保障的過程中，由于艦船甲板空間不足、備件不足、機務人員不足等原因導致的直升機不能及時得到保障的問題，將這些因素抽象為艦船上保障點不可用，提出了一種基于干擾模型的機群保障點失效應急重構策略生成方法。

1) 對機群保障系統保障點失效的情況做出假設，定義相應的參數和變量。

2) 應用拉格朗日松弛算法，建立目標函數的拉格朗日對偶模型，并結合次梯度算法得出一組目標值。

3) 利用啟發式算法，給出松弛條件下較優的機群保障調整方案。

參考文獻：

[1] 袁 俊.淺析軍機的綜合保障費用[J].航空標準化和質量，2013,56(4):15-17.

[2] Kevin L B. Understanding the empirical hardness of NP-complete problems[J]. Communications of the ACM,2014,57(5):98-107.

[3] Maksimenko A N.The simplest families of polytopes associated with NP-hard problems[J]. Doklady Mathematics,2015,9(1):53-55.

[4] 康 寧,武小悅. 航天測控調度問題的拉格朗日啟發式算法[J].火力指揮與控制, 2012,3(8):104-107.

[5] LI B C，Dang C Y，ZHENG J J. A distributed integer programming for recovering[J]. Computer Application and Software, 2014,31(12):80-84.