一種采用可重構極化旋轉表面的天線RCS減縮方法

王夫蔚， 李 珂， 任宇輝

(西北大學 信息科學與技術學院，陜西 西安 710127)

雷達截面(Radar Cross Section， RCS)是表征物體散射特性的重要指標，是指電磁波照射時物體在某一方向上返回散射功率的量度．雷達截面既與目標的材料、尺寸、形狀、結構等幾何或物理參數相關，也與照射電磁波的參數有關，同時目標和電磁波夾角也會對雷達截面造成影響[1-2]．飛行器和艦艇的雷達隱身性能主要取決于它們雷達截面的大小，其隱身技術主要集中在通過各種方法減小飛行器和艦艇對雷達探測波的有效散射截面上，達到降低敵方雷達作用距離的目的．

天線系統作為武器平臺通信、作戰環節的重要組成部分，必不可少地分布于武器或目標平臺的各個位置．更進一步考慮，對于武器平臺本身雷達截面已經很大程度降低以后，其天線的雷達截面則相對較為明顯，天線的雷達截面控制問題也就逐漸顯現，最終使得天線的隱身性能成為影響整體平臺隱身性能好壞的一個重要因素．與一般目標平臺不同的是，天線首先要保證自身良好的性能，即輻射性能，這就導致常規的目標隱身方式(外形設計，吸波材料等)直接應用于天線隱身當中時會遇到很多問題．因此，天線系統隱身性能的好壞，就成為整體作戰平臺隱身技術中亟待解決的關鍵問題之一[3-5]．

由于極化旋轉表面(Polarization Rotation Surfaces， PRS)能夠改變入射波的極化方向，逐漸地出現在天線的雷達截面減縮研究中[6-7]．極化旋轉表面在用于天線或普通金屬目標的雷達截面減縮時，首先電磁波入射至極化旋轉表面并反射，利用棋盤式分布使得不同區域內的反射波極化相反(即存在180°的相位差)，則不同區域的反射波在反射后由于相位差而相互抵消，進而降低了該部分的雷達截面．但是極化旋轉表面在天線雷達截面減縮中使用時，會造成天線本身剖面的增大以及破壞輻射特性等情況，阻礙了極化旋轉表面在天線雷達截面減縮中的進一步應用．

可重構技術是指通過具有動態可變的特定功能部件來實現系統在一定輸出信號作用下性能動態可調．近年來，可重構技術已經被成功地應用于天線的設計之中．早期的研究主要集中在通過調整輻射結構來改變電流分布進而達到天線輻射特性，例如工作頻率、方向圖以及極化的可重構[8-10]．與此同時，超材料由于其特殊的電磁特性越來越受到學者們的廣泛關注．現有的超材料研究主要以無源結構為主，將可重構理念用于超材料的設計并不多，且多集中在單純的超材料工作頻段變化的可重構技術方面．目前，將可重構超材料用于天線設計當中并不多見，尤其將可重構超材料用于天線的雷達截面減縮更是鮮有報道．

為了解決上述問題，同時基于各種綜合因素考慮，筆者提出將可重構極化旋轉表面作為天線反射板使用，使得極化旋轉表面通過二極管控制分為兩種狀態．當二極管處于導通狀態(即ON-state)時，極化旋轉表面的電磁波極化旋轉功能并不工作，則其與一般的金屬板無異，能夠最大限度地保證天線的輻射特性；當二極管處于截斷狀態(即OFF-state)時，極化旋轉表面正常工作，則該反射板處于低雷達截面狀態，天線的單站雷達截面得到了最大程度的縮減．

1 可重構極化旋轉表面

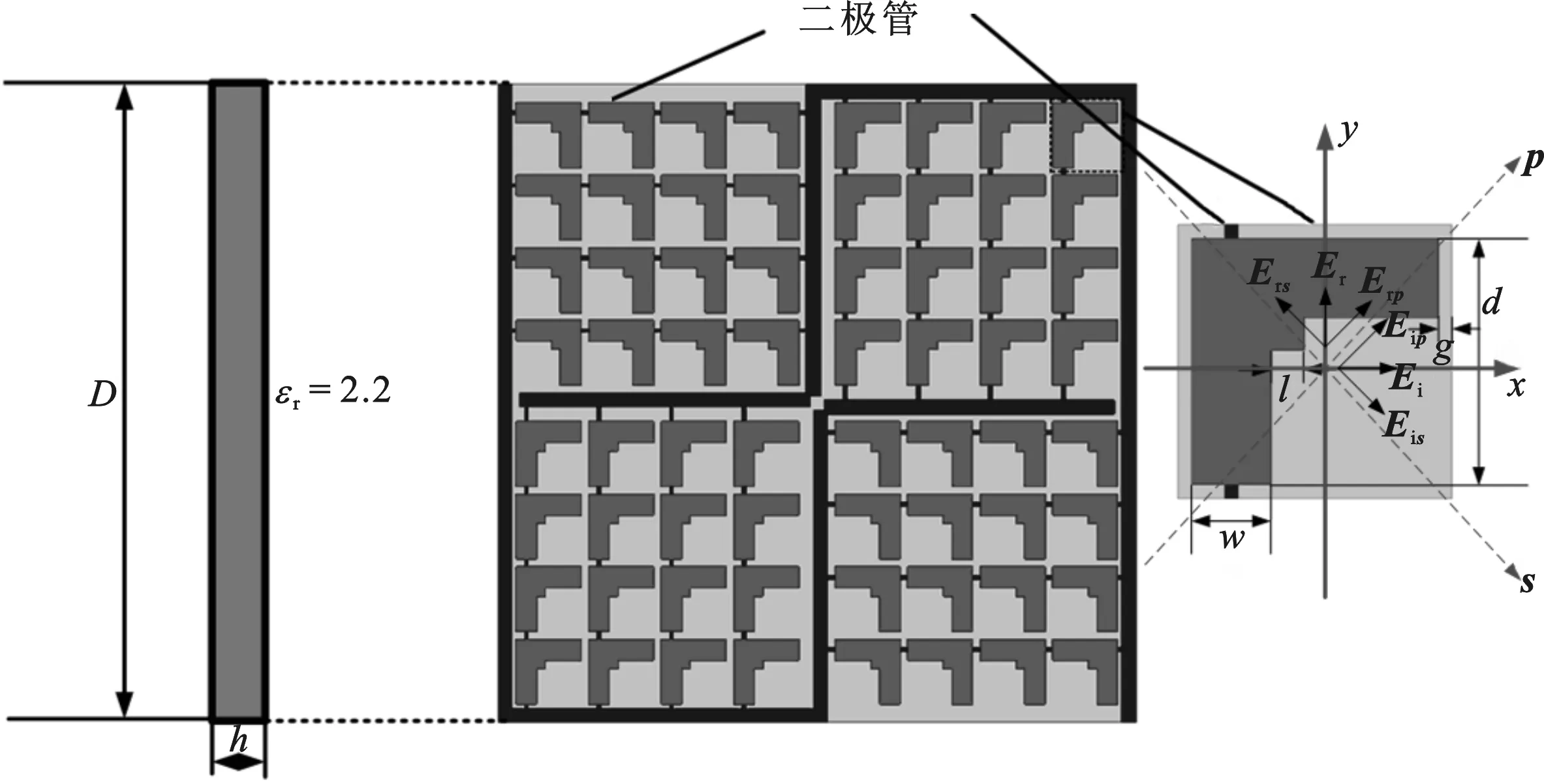
圖1 可重構極化旋轉表面示意圖

首先給出可重構極化旋轉表面的驗證仿真實例．圖1所示為所設計的可重構極化旋轉表面結構示意圖，極化旋轉表面的工作頻段為 6.4～ 10.3 GHz．極化旋轉表面是通過在雙面覆銅的聚四氟乙烯介質板上蝕刻出的，介質板介電常數為2.2，tanδ為 0.000 9，介質厚度為 2 mm．每個極化旋轉表面單元通過二極管相連，并通過貫穿于單元間的金屬線完成統一的偏置電壓加載．可重構極化旋轉表面的參數值如表1所示．如圖1所示，若入射波為線極化波，極化方向沿x方向，則該入射波沿 -z方向垂直入射．可將Ei分量分解為p和s兩個正交的、等幅、同相分量．因此，入射波電場為

(1)

其中，a表示電場在x、s和p方向上的單位矢量．

類似地，電磁波經過極化旋轉表面后將沿+z軸方向反射，反射波電場為

其中，Γ=Γexp(jφ)，表示反射系數；下標ss、ps、sp和pp分別表示p、s極化方向上的主極化分量和交叉極化分量．

由于單一分量的線極化波經反射后極化方向保持不變，則取Γps=Γsp=0．要使反射波電場Er轉換為y軸方向(和x方向的Ei相比旋轉90°)，其在p和s方向上的分量必須滿足幅度相同，且相位相反，即

Γss=Γpp=Γ， Δφ=φss-φpp=2nπ+π ．(3)

此時，有Er=ΓEi0exp(j(-kz+φpp))ay，最終x方向極化的入射波轉換成了y方向極化的反射波．

表1 極化旋轉表面參數值

圖2給出了二極管截斷或導通時，極化旋轉表面的反射系數變化情況．如圖2(a)所示，在二極管截斷時，極化旋轉表面的工作頻段為 6.4～ 10.3 GHz，實線為主極化，虛線為交叉極化．在工作頻段內，電磁波均能夠有效地由主極化轉換為交叉極化．在二極管截斷時，如圖1所示的排布方式使得散射波在空中抵消，最終達到雷達截面減縮的目的．圖2(b)所示為二極管導通情況下的反射系數，其中主極化反射系數大于 -0.1 dB，交叉極化反射系數小于 -15 dB，則在二極管導通時該反射板與一般的金屬板無異．因此，該反射板可以在金屬板與低雷達截面反射板間相互切換．

圖3所示為二極管截斷或導通時，極化旋轉表面的反射系數隨入射角變化的情況．隨著入射波與法線夾角逐漸增大，入射波的電場方向發生改變．此時，入射波電場方向并不沿x軸方向，或在x方向只存在x分量．因此，經過極化旋轉表面后沿y軸方向的電場也僅為y分量．隨著角度變大，x以及y方向分量逐漸減小，所以隨著角度變化，極化旋轉特性會逐漸變差．可以看出，隨著角度的逐漸變大，極化旋轉表面的極化轉化特性逐漸減弱，但是在入射波角度小于45°的情況下，主極化反射系數均能維持在 -5 dB 以下．

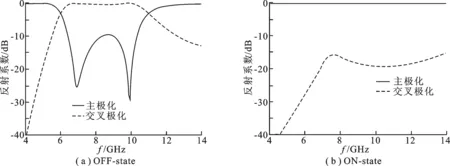
圖2 可重構極化旋轉表面反射系數

圖3 可重構極化旋轉表面反射系數隨角度變化的曲線

圖4 使用可重構極化旋轉表面反射板以及金屬反射板的天線實物圖

圖5 準八木天線結構圖

2 可重構極化旋轉表面在天線雷達截面減縮中的應用

為了說明該方案的有效性，針對之前給出的可重構極化旋轉表面模型，使用可重構極化旋轉表面置換金屬反射板的方法，對使用前后準八木天線的輻射散射特性進行分析．圖4所示分別為準八木天線使用普通金屬板、可重構極化旋轉表面反射板的實物圖．圖5所示為準八木天線結構圖，天線的基本參數如表2所示．

表2 準八木天線參數值

圖6 準八木天線S11比對曲線

當天線處于工作狀態(即二極管處于ON-state狀態)時，分別仿真及實測了準八木天線使用普通金屬板以及筆者所提出的可重構極化旋轉表面的性能．圖6所示為使用兩種反射板時天線的仿真及實測S11，可以看出天線的工作頻帶為 6.3～ 10.3GHz，且使用兩種反射板時的S11基本保持不變．圖7所示為使用兩種反射板時準八木天線的輻射方向圖實測結果．如圖中所示，使用可重構極化旋轉表面后準八木天線的輻射方向圖與使用金屬反射板的天線輻射方向圖吻合良好，天線增益損失約 0.5dB．由以上分析可得，在天線的工作頻帶內，使用ON-state狀態下的頻率選擇表面反射板能夠最大限度地保證天線的輻射性能．

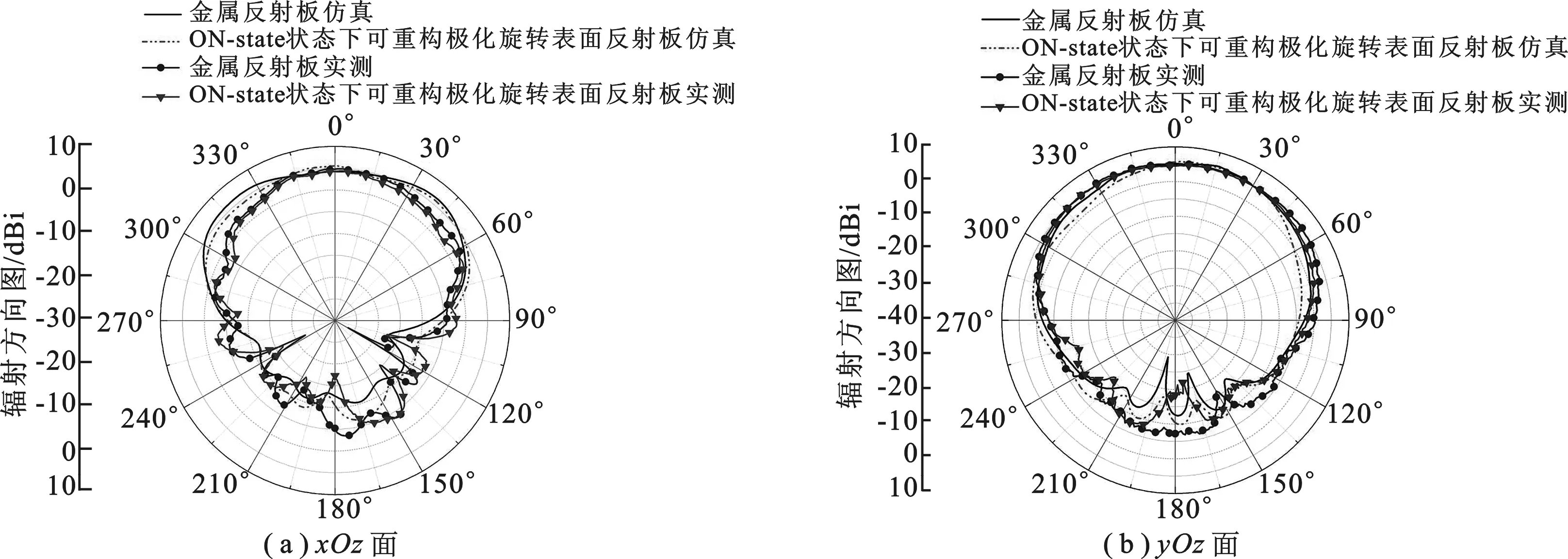
圖7 天線輻射方向圖比對曲線

為了驗證使用可重構極化旋轉表面的雷達截面減縮效果，對可重構極化旋轉表面的單站雷達截面進行仿真以驗證方法的有效性．設置入射波沿天線結構表面、垂直于反射板照射．在平面波照射下，天線的單站雷達截面隨頻率的變化如圖8所示．圖8(a)所示為φ極化下入射波照射的單站雷達截面對比曲線，從圖中可以看出，與理想電導體反射板相比，雷達截面在 6～ 12GHz范圍均有不同程度的縮減，其中在 6.8GHz時，最大縮減量可達 25dB．圖8(b)所示入射波為θ極化，雷達截面減縮頻段與圖8(a)中的類似，其中 6.8GHz時的最大減縮量可達 16dB．仿真結果說明，將可重構極化旋轉表面用于天線雷達截面減縮的方法是有效的．

圖8 單站雷達截面隨頻率變化的曲線

為了進一步說明使用該方法的雷達截面減縮效果，圖9及圖10給出了使用可重構極化旋轉表面反射板前后天線的單站雷達截面隨角度變化的仿真曲線，中心頻率為 9GHz．圖9所示入射波極化為φ極化．如圖9(a)所示，使用可重構極化旋轉表面反射板時，天線xOz面的雷達截面減縮區間為 -50°≤ θ≤ +50°，最大減縮量可達 10dB以上．圖9(b)給出了天線yOz面上雷達截面隨角度變化曲線，可以看出雷達截面的減縮區間為 -20°≤ θ≤ +20°．圖10所示入射波極化為θ極化，xOz面與yOz面上的準八木天線單站雷達截面均有不同程度的縮減，減縮區間為 -20°≤ θ≤ +20°．

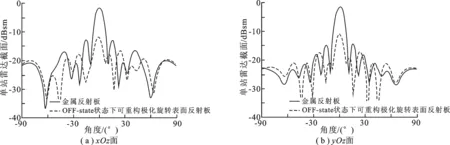
圖9 天線單站雷達截面隨角度變化比對曲線圖(入射波φ極化)

圖10 天線單站雷達截面隨角度變化比對曲線圖(入射波θ極化)

由圖9和圖10可以看出，在不同極化狀態下，使用可重構極化旋轉表面反射板的天線單站雷達截面峰值有所區別．這是由于入射波是垂直于反射板照射(也就是沿天線表面方向入射)，使用金屬反射板時天線系統可看成對稱結構，因此單站雷達截面峰值基本一致．而使用可重構極化旋轉表面反射板時，由于極化旋轉表面的單元結構以及棋盤式排布后的反射板均為非對稱結構，對于不同極化的入射波，散射特性會有明顯差異．因此，入射波為不同極化時，天線的單站雷達截面峰值會有明顯區別．綜上所述，當反射板處于OFF-state狀態時，天線雷達截面在一定角度范圍內均有明顯降低，具有良好的工程應用價值．

3 總 結

筆者提出一種采用可重構極化旋轉表面置換一般金屬反射板的方法，用以實現準八木天線的天線雷達截面減縮，并能夠最大限度地保留天線輻射性能．通過二極管對極化旋轉表面進行控制，使其能夠在一般金屬板以及低雷達截面板間相互切換．仿真及實測結果表明，在保證天線輻射特性不被破壞的同時，當使用可重構極化旋轉表面反射板時，準八木天線的單站雷達截面最大減縮可達 25 dB 以上，減縮角域為 -20°≤θ≤ +20°．

[1] KNOTT E F, SHAEFFER J F, TULEY M T. Radar Cross Section[M]. 2nd Edition. Raleigh: SciTech Publishing, 2004.

[2] POZAR D M. Radiation and Scattering from a Microstrip Patch on a Uniaxial Substrate[J]. IEEE Transactions on Antennas and Propagation, 1987, 35(6): 613-621.

[3] 王夫蔚, 龔書喜, 張鵬飛, 等. 結構型吸波材料在陣列天線RCS減縮中的應用[J]. 西安電子科技大學學報, 2012, 39(5): 91-95.

WANG Fuwei, GONG Shuxi, ZHANG Pengfei, et al. Radar Absorbing Material Applied to the RCS Reduction of Array Antennas [J]. Journal of Xidian University, 2012, 39(5): 91-95.

[4] 王夫蔚, 梁瑞香, 龔書喜, 等. 左手材料在天線角域RCS控制中的應用[J]. 西安電子科技大學學報, 2013, 40(6): 123-130.

WANG Fuwei, LIANG Ruixiang, GONG Shuxi, et al. Left-handed Metamaterial Applied to the RCS Reduction of Antenna[J]. Journal of Xidian University, 2013, 40(6): 123-130.

[5] WANG F W, JIANG W, HONG T, et al. Radar Cross Section Reduction of Wideband Antenna with a Novel Wideband Radar Absorbing Materials[J]. IET Microwaves, Antennas and Propagation, 2014, 8(7): 491-497.

[6] LIU Y, LI K, JIA Y T, et al. Wideband RCS Reduction of a Slot Array Antenna Using Polarization ConversionMetasurfaces[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(1): 306-331.

[7] JIA Y T, LIU Y, GUO Y J, et al. Broadband Polarization Rotation Reflective Surfaces and Their Applications to RCS Reduction[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(1): 179-188.

[8] ALVAREZ C N, CHEUNG R, THOMPSON J S. Performance Analysis of Hybrid Metal-graphene Frequency Reconfigurable Antennas in the Microwave Regime[J]. IEEE Transactions on Antennas and Propagation, 2017, 65(4): 1558-1569.

[9] HORESTANI A K, SHATERIAN Z, NAQUI J, et al. Reconfigurable and Tunable S-shaped Split-ring Resonators and Application in Band-notched UWB Antennas[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(9): 3766-3776.

[10] ZHANG M T, GAO S, JIAO Y C, et al. Design of Novel Reconfigurable Reflectarrays with Single-bit Phase Resolution for Ku-band Satellite Antenna[J]. IEEE Transactions on Antennas and Propagation, 2016, 64(5): 1634-1641.