非共振圓偏振光作用下單層二硫化鉬電子結構及其自旋/谷輸運性質?

張新成 廖文虎 左敏

(吉首大學物理與機電工程學院,吉首 416000)

1 引 言

近10多年來,以石墨烯為代表的二維材料因為其優異的物理性質和器件設計方面的應用前景引起了物理、材料、信息等領域的廣泛關注[1,2].邊緣功能化[3]、微納結構化[4]、化學摻雜[5]等方法能夠在一定程度上打開石墨烯的帶隙,但無帶隙的本征能帶結構[6,7]使得石墨烯基場效應晶體管截止電流較高、電流開關比較低[8].與石墨烯幾何結構類似的單層二硫化鉬(MoS2)是直接帶隙半導體,具有自旋/谷霍爾效應等物理特性[9?13],從器件設計和應用角度看比石墨烯更加優異,近年來成為新型半導體材料的研究熱點之一[14?20].

2011年,Kis等[14]成功地制備了單層MoS2場效應晶體管,后來Liu研究組[15]采用原子層沉積技術成功制作出遷移率高達517 cm2/(V·s)的MoS2場效應晶體管,Zhang等[16]利用離子液體作為柵極制造出具有較高空穴遷移率的單層MoS2場效應晶體管.2012年,Xiao等[17]和Cao等[18]發現單層MoS2在六邊形布里淵區頂點附近具有“谷”狀能帶結構,相鄰頂點的谷對左、右旋光具有近乎完美的選擇性.香港大學和哥倫比亞大學的實驗組通過圓偏振光抽運方法驗證了單層MoS2具有偏振光選擇性和谷霍爾效應[19,20].2016年,Sengupta和Bellotti[21]研究了非共振圓偏振光作用下二維過渡族金屬硫化物自旋霍爾電導,單層MoS2在應力和磁近鄰交換場作用下的輸運性質也受到關注[22,23],外部電場和近鄰交換相互作用被證明是調控單層MoS2能帶結構[24?26]的有效手段.然而,很少有相關工作涉及外部非共振圓偏振光對單層MoS2電子能帶結構和自旋/谷輸運特性的影響,本文針對這方面的問題開展研究.

利用緊束縛近似下的低能有效哈密頓模型和久保線性響應理論,研究了外部非共振圓偏振光對單層MoS2電子能帶結構及其自旋/谷輸運性質的影響.研究結果表明:單層MoS2布里淵區K谷和K′谷附近自旋依賴的子帶間能隙隨著非共振右旋圓偏振光引起的有效耦合能分別線性增大和先減小后增大,隨著非共振左旋圓偏振光引起的有效耦合能分別先減小后增大和線性增大,實現了有趣的半導體-半金屬-半導體轉變.在沒有非共振圓偏振光作用時,單層MoS2量子化自旋霍爾電導為0、谷霍爾電導為2e2/h;當非共振圓偏振光有效耦合能絕對值在0.79—0.87 eV范圍內變化時,系統自旋霍爾電導為?2e2/h、谷霍爾電導為0;當非共振圓偏振光引起的有效耦合能在其他范圍內變化時,量子化自旋/谷霍爾電導與無外場時相同.系統自旋極化率在非共振圓偏振光有效耦合能±0.79 eV附近達到最大并發生由正到負或由負到正的急劇轉變,谷極化率隨著非共振圓偏振光有效耦合能先增大后減小,在非共振圓偏振光有效耦合能絕對值0.79—0.87 eV范圍內達到100%.因此,外部非共振圓偏振光是調控單層MoS2量子化霍爾電導、自旋/谷霍爾電導以及自旋/谷極化的有效手段.

2 模型與方法

如圖1所示,我們構建了一個基于單層MoS2的場效應晶體管模型,其中單層MoS2置于中心區域并受到非共振圓偏振光的輻照,系統有效哈密頓量為[10,17,27,28]

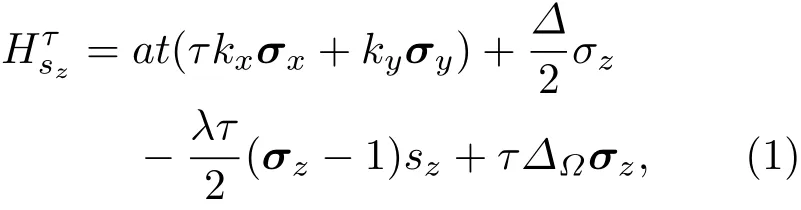
此外,非共振圓偏振光引起的電磁勢可以描述為

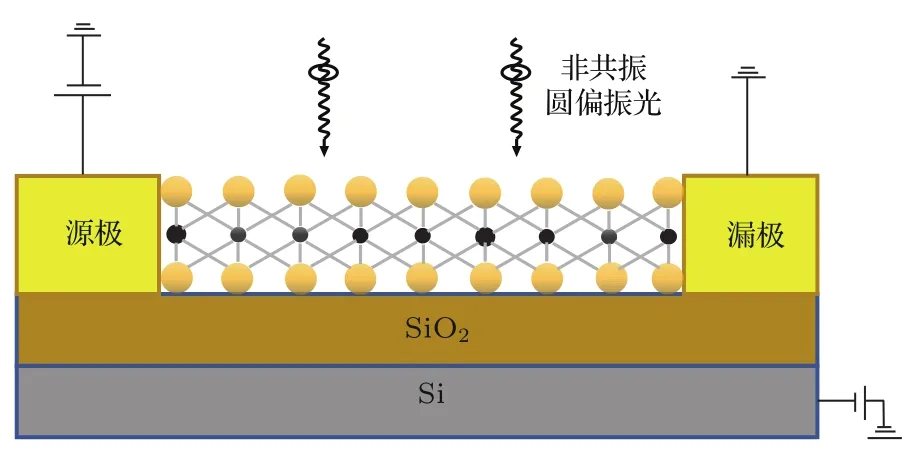
圖1 由金屬源極、漏極和可調制背電極構成MoS2納米場效應管模型圖,其中心區域受到非共振圓偏振光的輻照,黑色小球代表鉬原子(Mo),黃色小球代表硫原子(S)Fig.1.Schematic representation of the MoS2based fi eld e ff ect transistor,consisting of metallic source,drain and electrically modulated back-gate,with the central region irradiated by the o ff-resonant circularly polarized light(demonstrated by the wave lines),and the black and yellow balls indicates the molybdenum(Mo)and sulfur(S)atoms,respectively.

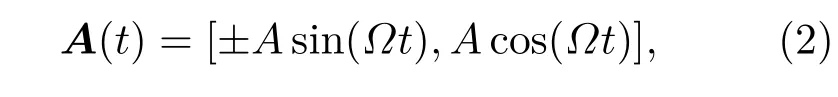
其中+和?分別表示右旋和左旋圓偏振光,?為非共振圓偏振光的頻率,A為非共振圓偏振光的振幅.電磁勢滿足時間周期性條件,即A(t+T)=A(t),周期T=2π/?.通過正則變換獲得非共振圓偏振光輻照對體系的影響,含時哈密頓量為

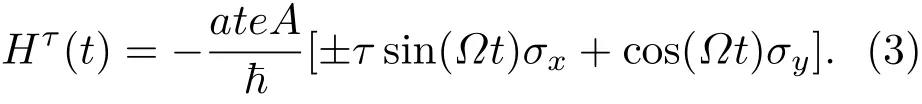
當非共振圓偏振光光子能量遠大于最近鄰躍遷能時,非共振圓偏振光對體系的影響可通過Floquet理論[28,29]簡化為有效靜態(不含時的)哈密頓量?Hτ.非共振圓偏振光屬于高頻弱場,不直接激發體系中的電子,而是通過光子吸收和發射過程改變體系的電子能帶結構.先吸收光子后發射光子過程中對體系哈密頓量的改變為,其中分別為電子能量和光子能量,先發射光子后吸收光子過程中對體系哈密頓量的改變為,其中,

因此,非共振圓偏振光對體系電子能帶結構的影響[28,30]為

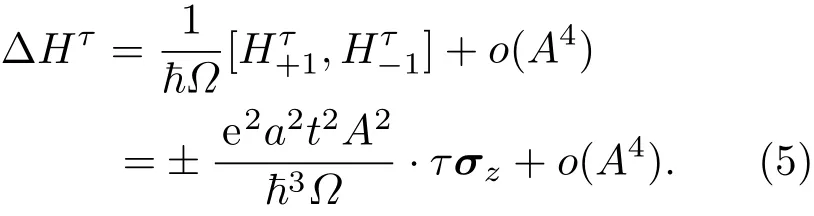
忽略高階小量后,獲得非共振圓偏振光輻照引起的有效耦合能??=±a2t2e2A2/h3?,其中+和?分別表示右旋和左旋圓偏振光.

通過對角化公式(1)中的哈密頓量,可以得到如下色散關系:

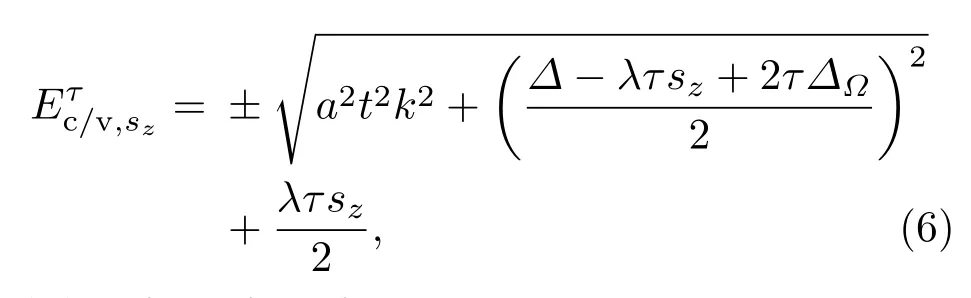
其中,,根號外的+和?分別對應導帶(c)和價帶(v),對應的導帶與價帶波函數分別為

我國對農業機械的需求量較大，然而在相關技術研發方面的投入卻與需求量不成比例，其中技術研發人員、研發基礎技術、研發所需設備缺口量較大，導致我國農業機械技術的研發進度相對遲緩，無法滿足我國農業機械化發展的需求。

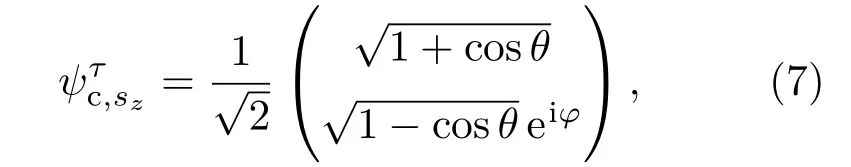
和

利用久保線性響應理論[31?34],可以得到自旋和谷依賴的橫向霍爾電導:

其中S為系統面積,

為費米-狄拉克分布函數,η為無窮小量.可以進一步得到系統的自旋霍爾電導[35,36]

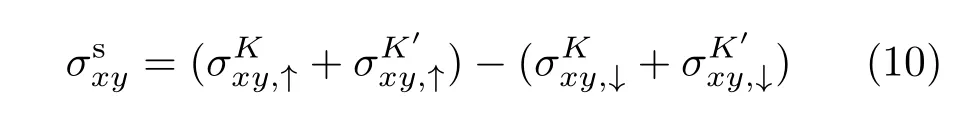
和谷霍爾電導

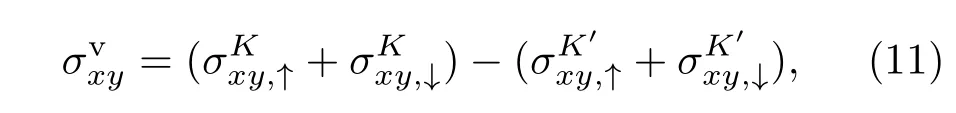
其中↑和↓分別表示自旋向上和自旋向下.

此外,系統的縱向電導[32,33]為

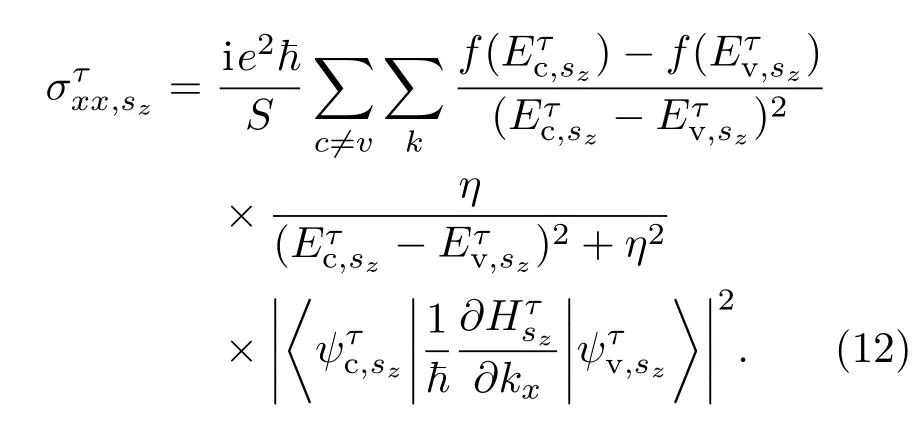
根據縱向電導,可以進一步得到系統自旋極化率

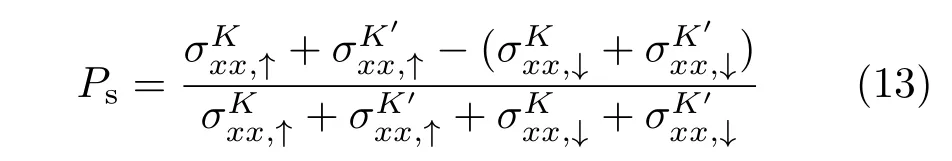
和谷極化率[37]

3 結果與討論

由于MoS2谷電子對光的手性選擇性,使得特定振幅和頻率的非共振右旋或左旋圓偏振光只能修飾K谷或K′谷的電子,從而產生能隙的變化,但是此時的能隙不是平衡態布洛赫電子的能隙,而是非平衡態Floquet能隙.圖2給出了單層MoS2布里淵區K/K′谷附近自旋依賴的價帶與導帶子帶間能隙隨非共振圓偏振光引起的有效耦合能的變化關系.系統布里淵區K谷附近自旋向上、向下價帶與導帶間的能隙(如圖2中正能段黑色實線和紅色虛線所示)隨著非共振右旋圓偏振光引起的有效耦合能增強呈線性增大,布里淵區K′谷附近自旋向上、向下價帶與導帶間的能隙(如圖2中正能段藍色點虛線和綠色點線所示)隨著非共振右旋圓偏振光引起的耦合能增強先減小后增大,在非共振右旋圓偏振光引起的耦合能0.79和0.87 eV附近自旋向上和向下價帶與導帶間的能隙減小到趨于0,此時MoS2表現出半金屬性.此外,單層MoS2布里淵區K谷附近價帶與導帶間的能隙隨非共振左旋圓偏振光引起的有效耦合能先減小后增大(如圖2中負能段黑色實線和紅色虛線所示),在非共振左旋圓偏振光引起的耦合能?0.79和?0.87 eV附近發生半導體-半金屬相變,K′谷附近自旋向上、向下價帶與導帶間的能隙(如圖2中負能段藍色點虛線和綠色點線所示)隨著非共振左旋圓偏振光引起的有效耦合能增強線性增大.由此可見,外部非共振圓偏振光可引起單層MoS2能帶結構有趣的半導體-半金屬-半導體轉變,從而引起系統自旋/谷輸運特性的有趣變化(如圖3—圖6所示).

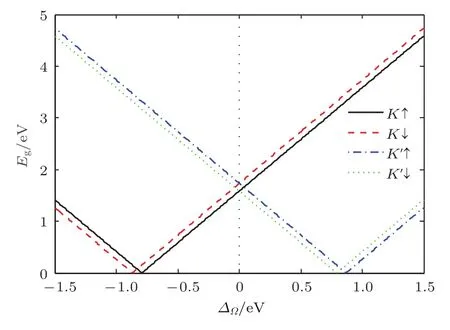
圖2 單層MoS2在K/K′谷附近價帶與導帶間能隙(以eV為單位)隨非共振圓偏振光引起的有效耦合能??的變化關系,其中黑色實線和紅色虛線分別表示K谷附近自旋向上和自旋向下價帶與導帶間的能隙,藍色點虛線和綠色點線分別表示K′谷附近自旋向上和自旋向下價帶與導帶間的能隙Fig.2.Energy gap Eg(in units of eV)of the monolayer MoS2as a function of the effective coupling energy??induced from the external of f-resonant circularly polarized light where the(black)solid and(red)dashed line demontrates energy gap from the spin-up and-down subbands at the vicinity of K valley,while that for the K′valley is denoted by the(blue)dasheddot and(green)dot line,respectively.

利用久保線性響應理論,進一步研究了非共振圓偏振光作用下單層MoS2的量子化橫向霍爾電導.當MoS2費米能級處于價帶與導帶間的帶隙中時,系統自旋/谷依賴的橫向霍爾電導趨于量子化[24,32,35].如圖3所示,系統橫向霍爾電導在非共振右旋、左旋圓偏振光作用下的變化規律類似.下面以單層MoS2在非共振右旋圓偏振光作用下的情形為例展開討論.當非共振右旋圓偏振光引起的耦合能在0—0.79 eV以及0.87—1.50 eV范圍內變化時,如圖3所示,單層MoS2布里淵區K谷和K′谷自旋向上量子化霍爾電導分別為e2/2h和?e2/2h;當非共振右旋圓偏振光引起的耦合能在0.79—0.87 eV范圍內變化時,K谷自旋向上量子化霍爾電導由e2/2h為?e2/2h、自旋向下量子化霍爾電導仍為e2/2h(如圖3(a)中正能段黑色實線和紅色虛線所示),K′谷自旋向上橫向量子化霍爾電導為?e2/2h、自旋向下量子化霍爾電導由?e2/2h躍變為e2/2h(如圖3(b)中正能段藍色點虛線和綠色點線所示).

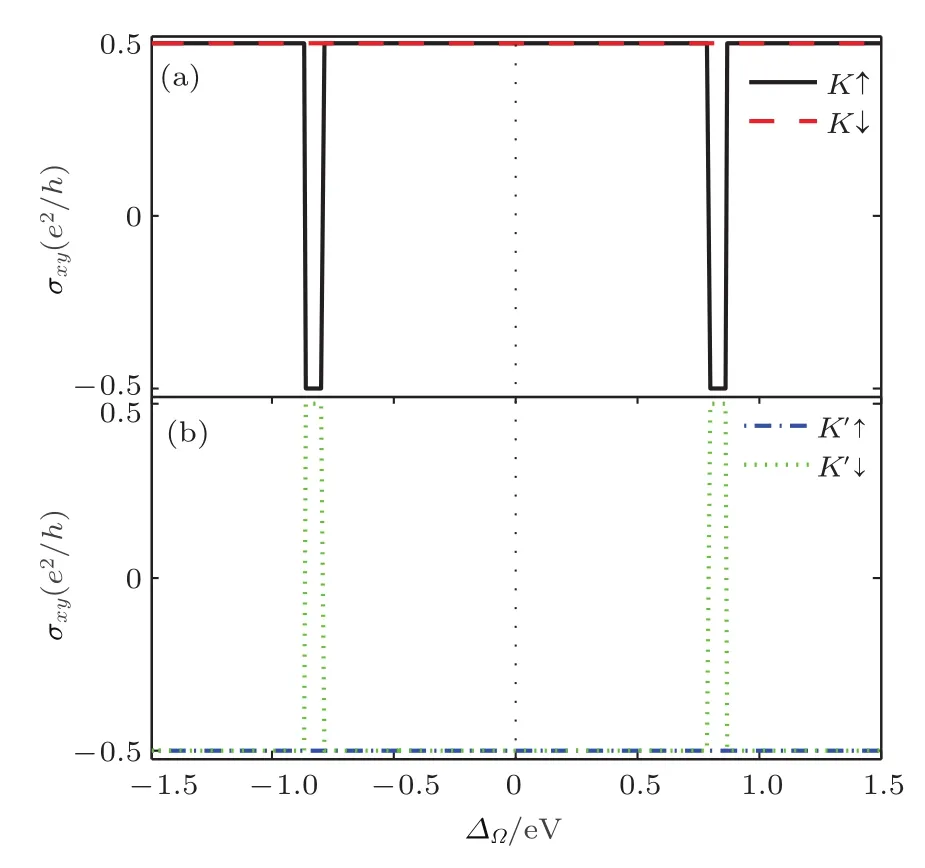
圖3 單層MoS2橫向霍爾電導(以e2/h為單位)隨非共振圓偏振光引起的有效耦合能??的變化關系 (a)黑色實線和紅色虛線分別表示K谷附近自旋向上和自旋向下橫向霍爾電導;(b)藍色點虛線和綠色點線分別表示K′谷附近自旋向上和自旋向下橫向霍爾電導Fig.3.Transversal Hall conductance σxy(in units of e2/h)of the monolayer MoS2as a function of the effective coupling energy??induced from the external of f-resonant circularly polarized light:(a)The(black)solid and(red)dashed line denotes the spin-up and-down transversal Hall conductance at the vicinity of K valley,while that for K′valley in(b)is illustrated by the(blue)dashed-dot and(green)dot line,respectively.

圖4 單層MoS2橫向量子化自旋霍爾電導(以e2/h為單位)和谷霍爾電導(以e2/h為單位)隨非共振圓偏振光引起的有效耦合能??的變化關系,其中黑色實線和紅色虛線分別表示自旋霍爾電導和谷霍爾電導Fig.4.Transversal quantized spin conductance σsxy(in units of e2/h)and σvxy(in units of e2/h)of the monolayer MoS2as a function of the effective coupling energy??induced from the external of f-resonant circularly polarized light,as has been denoted by the(black)solid and(red)dashed line,respectively.

圖4給出了單層MoS2量子化自旋霍爾電導(黑色實線所示)和谷霍爾電導 (紅色虛線所示)隨非共振圓偏振光引起的有效耦合能的變化.非共振左旋圓偏振光引起的有效耦合能在?1.50—?0.87 eV范圍內變化時,系統量子化自旋霍爾電導為0(如圖4中黑色實線所示)、谷霍爾電導為2e2/h(如圖4中紅色虛線所示).有趣的是,當非共振左旋圓偏振光引起的有效耦合能在?0.87—?0.79 eV范圍內變化時,如圖4中黑色實線和紅色虛線所示,系統自旋霍爾電導為?2e2/h、谷霍爾導由2e2/h躍變為0.當非共振光左電旋圓偏振光引起的有效耦合能在?0.79—0 eV范圍內變化時,系統自旋霍爾電導消失、谷霍爾電導從0躍變到2e2/h.此外,如圖4中黑色實線所示,當非共振光右旋圓偏振光引起的有效耦合能在0.79—0.87 eV范圍內變化時,系統自旋霍爾電導從0—0.79 eV范圍內的0躍變到?2e2/h、谷霍爾電導(如圖4中紅色虛線所示)由2e2/h躍變為0.當非共振光右旋圓偏振光引起的耦合能在0.87—1.50 eV范圍內變化時,系統自旋霍爾電導為0、谷霍爾電導(如圖4中紅色虛線所示)由0躍變到2e2/h.因而,系統量子化自旋霍爾電導和谷霍爾電導[24,35]敏感地依賴于電子的自旋/谷自由度以及外部非共振光偏振光引起的有效耦合能.

進一步研究了單層MoS2縱向電導隨非共振圓偏振光引起的有效耦合能的變化關系.如圖5中的黑色實線和紅色虛線所示,單層MoS2布里淵區K谷附近自旋向上、向下縱向電導在非共振光左旋圓偏振光引起的耦合能?0.79和?0.87 eV附近呈現共振峰(共振峰的能量位置與圖2中的半導體-半金屬相變能量點以及圖3中的K谷橫向霍爾電導躍變能量對應).另外,如圖5中藍色點虛線和綠色點線所示,單層MoS2布里淵區K′谷附近自旋向上、向下縱向電導在非共振光右旋圓偏振光引起的耦合能0.79和0.87 eV附近呈現共振峰,共振峰的能量位置與圖2中的相變能量點以及圖3中的K′谷橫向霍爾電導躍變能量一一對應.

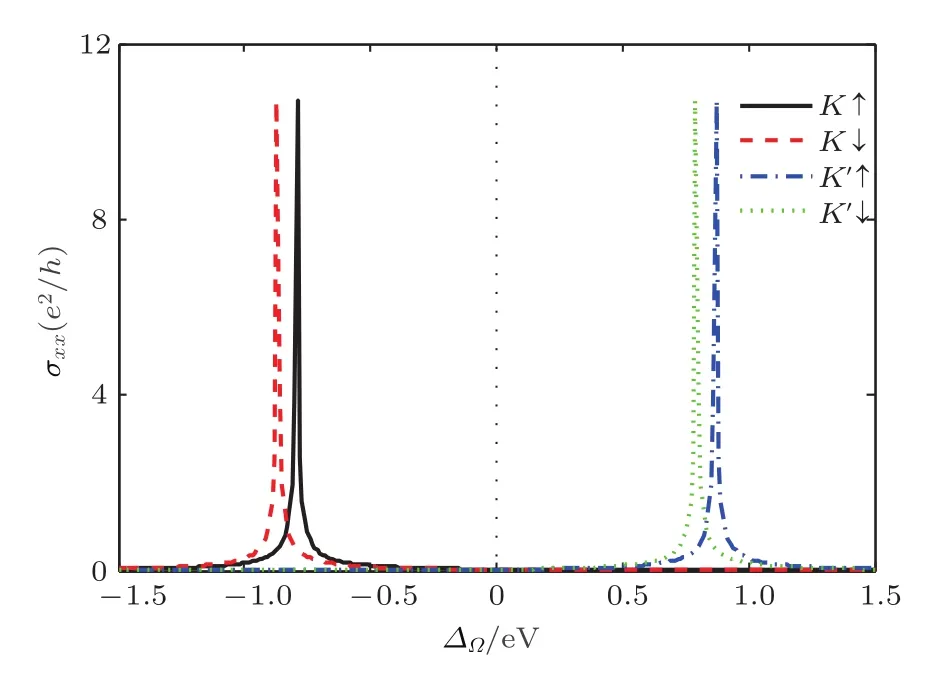
圖5 單層MoS2布里淵區K/K′谷附近縱向電導(以e2/h為單位)隨非共振圓偏振光引起的耦合能??的變化關系,其中黑色實線、紅色虛線分別表示K谷附近自旋向上、自旋向下縱向電導,藍色點虛線和綠色點線分別表示K′谷附近自旋向上和自旋向下縱向電導Fig.5. Longitudinal conductance σxx(in units of e2/h)at the vicinity of K/K′valley for monolayer MoS2as a function of the effective coupling energy??induced from the external of f-resonant circularly polarized light,where the(black)solid and(red)dashed line denotes the spin-up and-down longitudinal conductance at the vicinity of K valley,while the(blue)dashed-dot and(green)dot line gives the spin-up and-down longitudinal conductance at the vicinity of K′valley,respectively.

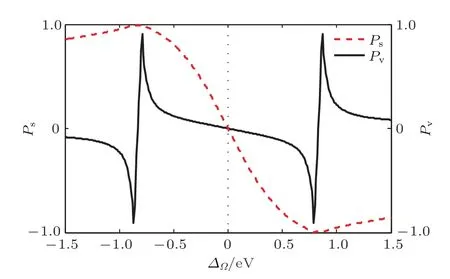
圖6 單層MoS2縱向電導自旋極化率Ps和谷極化率Pv隨非共振圓偏振光引起的有效耦合能??的變化關系,其中黑色實線和紅色虛線分別表示自旋極化率Ps和谷極化率PvFig.6.Longitudinal conductance spin and valley polarization rate(denoted by Psand Pv,respectively)for monolayer MoS2as a function of the effective coupling energy??induced from the external of f-resonant circularly polarized light,as has been illustrated by the(black)solid and(red)dashed line,respectively.

圖6給出了單層MoS2自旋極化率和谷極化率隨非共振圓偏振光引起的耦合能的變化關系.非共振左旋圓偏振光引起的耦合能在?0.79—0 eV范圍內變化時,系統自旋極化率(如圖6中負能段黑色實線所示)隨著非共振左旋圓偏振光引起的耦合能增強先慢后快增大,在非共振左旋圓偏振光引起的耦合能?0.79 eV附近呈現由正到負的急劇轉變,系統谷極化率(如圖6中負能段紅色虛線所示)先隨著非共振左旋圓偏振光引起的耦合能增強先快后慢增大,在非共振左旋圓偏振光有效耦合能?0.87—?0.79 eV范圍內達到100%,然后隨著非共振圓偏振光有效耦能增強緩慢減小(谷極化率一直保持在90%以上).此外,當非共振右旋圓偏振光引起的耦合能在0—0.79 eV范圍內變化時(如圖6中正能段黑色實線所示),系統自旋極化率隨著非共振右旋圓偏振光引起的耦合能增強先慢后快增強,在非共振右旋圓偏振光引起的耦合能為0.79 eV附近呈現由負到正的急劇轉變,系統谷極化率(如圖6中正能段紅色虛線所示)先隨著非共振右旋圓偏振光引起的耦合能增強先快后慢增大,在非共振右旋圓偏振光有效耦合能0.79—0.87 eV范圍內達到100%,然后隨著非共振圓偏振光引起的有效耦合能增強緩慢減小(谷極化率一直超過90%).可見,利用非共振圓偏振光有望在單層MoS2上實現100%的谷極化,從而用于谷電子器件設計;在特定非共振圓偏振光引起的有效耦合能附近實現系統自旋極化的急速反轉,這對基于MoS2的新型高速自旋電子器件設計具有一定的指導意義.

4 結 論

利用緊束縛近似下的低能有效哈密頓模型和久保線性響應理論,研究了外部非共振圓偏振光對單層MoS2電子能帶結構、橫向霍爾電導、縱向電導及其自旋/谷輸運性質的影響.研究結果表明,單層MoS2布里淵區K谷和K′谷附近能隙隨著非共振右旋圓偏振光引起的有效耦合能增強分別呈線性增大和先減小后增大,隨著非共振左旋圓偏振光引起的有效耦合能增強分別先減小后增大和線性增大,實現有趣的半導體-半金屬-半導體轉變.此外,非共振圓偏振光有效耦合能絕對值在0.79—0.87 eV范圍內變化時,系統自旋霍爾電導為?e2/2h、谷霍爾電導消失.在非共振右/左旋圓偏振光有效耦合能±0.79 eV附近,系統自旋極化率呈現由負到正或由正到負的急劇轉變.系統谷極化率隨著非共振左旋和右旋圓偏振光有效耦合能增強而增大,在非共振圓偏振光有效耦合能絕對值0.79—0.87 eV范圍內接近于100%.總之,外部非共振圓偏振光是調控單層MoS2量子化霍爾電導、自旋/谷霍爾電導以及縱向電導自旋/谷極化的有效手段,可利用外部電磁場實現單層MoS2完全谷極化或自旋極化,為基于低維過渡族金屬硫化物的新型高速自旋/谷電子器件設計提供理論基礎.

[1]Novoselov K S,Geim A K,Morozov S V,Jiang D,Zhang Y,Dubonos S V,Grigorieva I V,Firsov A A 2004Science306 666

[2]Novoselov K S,Geim A K,Morozov S V,Jiang D,Katsnelson M I 2005Nature438 197

[3]Balog R,J?rgensen B,Nilsson L,Andersen M,Rienks E,Bianchi M,Fanetti M,Laegsgaard E,Baraldi A,Lizzit S,Sljivancanin Z,Besenbacher F,Hammer B,Pedersen T G,Hofmann P,Hornekaer L 2010Nature Mater.9 315

[4]Li X,Wang X,Zhang L,Lee S,Dai H 2008Science319 1229

[5]Zhou S Y,Gweon G H,Fedorov A V,First P N,de Heer W A,Lee D H,Guinea F,Castro Neto A H,Lanzara A 2007Nature Mater.6 770

[6]Xia F,Farmer D B,Lin Y,Avouris P 2010Nano Lett.10 715

[7]Guinea F,Katsnelson M I,Geim A K 2010Nat.Phys.6 30

[8]Chen J H,Jang C,Xiao S,Ishigami M,Fuhrer M S 2008Nat.Nanotechnol.3 206

[9]Li Z,Carbotte J P 2012Phys.Rev.B86 205425

[10]Majidi L,Rostami H,Asgari R 2014Phys.Rev.B89 045413

[11]Splendiani A,Sun L,Zhang Y,Li T,Kim J,Chim C Y,Galli G,Wang F 2010Nano Lett.10 1271

[12]Wang Q H,Kalantar-Zadeh K,Kis A,Coleman J N,Strano M S 2012Nat.Nanotechnol.7 699

[13]Mak K F,Lee C,Hone J,Shan J,Tony F H 2010Phys.Rev.Lett.105 136805

[14]Radisavljevic B,Radenovic A,Brivio J,Giacometti V,Kis A 2011Nat.Nanotechnol.6 147

[15]Liu H,Peide D Y 2012IEEE Electron Dev.Lett.33 546

[16]Zhang Y,Ye J,Matsuhashi Y,Iwasa Y 2012Nano Lett.12 1136

[17]Xiao D,Liu G B,Feng W X,Xu X D,Yao W 2012Phys.Rev.Lett.108 196802

[18]Cao T,Wang G,Han W P,Ye H Q,Zhu C R,Shi J R,Niu Q,Tan P H,Wang E G,Liu B L,Feng J 2012Nat.Commun.3 887

[19]Mak K F,He K,Shan J,Heinz T F 2012Nat.Nanotechnol.7 494

[20]Zeng H,Dai J,Yao W,Xiao D,Cui X 2012Nat.Nanotechnol.7 490

[21]Sengupta P,Bellotti E 2016Appl.Phys.Lett.108 211104

[22]Zheng H L,Yang B S,Wang D D,Han R L,Du X B,Yan Y 2014Appl.Phys.Lett.104 132403

[23]Yarmohammadi M 2017J.Magnet.Magnet.Mater.426 621

[24]Wang S,Wang J 2015Physica B458 22

[25]Yin Z Y,Li H,Li H,Jiang L,Shi Y M,Sun Y H,Lu G,Zhang Q,Chen X D,Zhang H 2012ACS Nano6 74

[26]Rostami H,Moghaddam A G,Asgari R 2013Phys.Rev.B88 085440

[27]Tahir M,Schwingenschlogl U 2014New J.Phys.16 115003

[28]Zhou L,Carbotte J P 2012Phys.Rev.B86 205425

[29]Kitagawa T,Oka T,Brataas A,Fu L,Demler E 2011Phys.Rev.B84 235108

[30]Kitagawa T,Broome M A,Fedrizzi A,Rudner M S,Berg E,Kassal I,Guzik A A,Demler E,White A G 2012Nat.Commun.3 882

[31]Tahir M,Manchon A,Sabeeh K,Schwingenschlogl U 2013Appl.Phys.Lett.102 162412

[32]Sinitsyn N A,Hill J E,Min H,Sinova J,MacDonald A H 2006Phys.Rev.Lett.97 106804

[33]Dutta P,Maiti S K,Karmakar S N 2012J.Appl.Phys.112 044306

[34]Cazalilla M A,Ochoa H,Guinea F 2014Phys.Rev.Lett.113 077201

[35]Tahir M,Manchon A,Schwingenschlogl U 2014Phys.Rev.B90 125438

[36]Feng W X,Yao Y G,Zhu W G,Zhou J J,Yao W,Xiao D 2012Phys.Rev.B86 165108

[37]Missault N,Vasilopoulos P,Vargiamidis V,Peeters F M,van Duppen B 2015Phys.Rev.B92 195423