基于廣義層間位移角譜的復(fù)合自復(fù)位結(jié)構(gòu)體系的參數(shù)分析
武大洋 呂西林
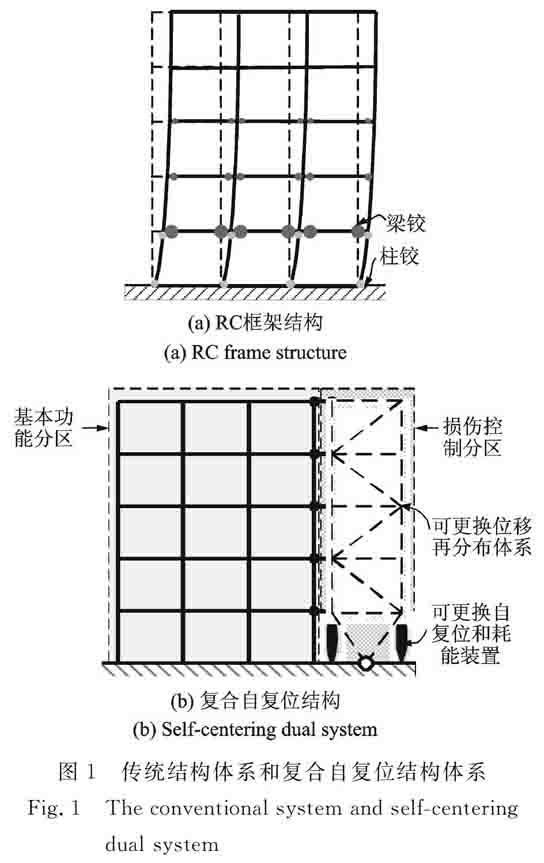


摘要: 提出了復(fù)合自復(fù)位結(jié)構(gòu)體系,該結(jié)構(gòu)體系在層次上由基本功能分區(qū)和損傷控制分區(qū)組成。根據(jù)不同分區(qū)的結(jié)構(gòu)變形特征將復(fù)合自復(fù)位結(jié)構(gòu)體系簡(jiǎn)化為由剪切梁和彎曲梁組成的雙梁分布體系模型。求解得到復(fù)合自復(fù)位結(jié)構(gòu)體系振型方程的閉合解,分析該體系在不同剪彎剛度比和彎曲梁與其底部約束剛度比下振型和振型轉(zhuǎn)角的變化規(guī)律。基于振型疊加法得到體系的廣義層間位移角譜,分析了剪彎剛度比和彎曲梁與其底部約束剛度比、阻尼比和高階模態(tài)對(duì)體系廣義層間位移角譜的影響。結(jié)果表明:在剪彎剛度比介于1~3的區(qū)間,彎曲梁與其底部約束剛度比介于1~5的區(qū)間,通過(guò)附加一定的阻尼,體系不僅可以抑制高階振型的影響得到較均勻的層間位移分布而且可以降低最大響應(yīng)。以廣義層間位移角譜為工具,可以實(shí)現(xiàn)復(fù)合自復(fù)位結(jié)構(gòu)體系直接基于位移的設(shè)計(jì)。
關(guān)鍵詞: 抗震結(jié)構(gòu); 復(fù)合體系; 自復(fù)位結(jié)構(gòu); 雙梁模型; 廣義層間位移角譜
中圖分類號(hào): TU352.1 文獻(xiàn)標(biāo)志碼: A 文章編號(hào): 1004-4523(2018)02-0255-10
DOI:10.16385/j.cnki.issn.1004-4523.2018.02.008
引 言
復(fù)合自復(fù)位結(jié)構(gòu)體系將地震作用下輸入結(jié)構(gòu)的能量集中于可更換的耗能構(gòu)件中,使結(jié)構(gòu)構(gòu)件在震后可以無(wú)需修復(fù)繼續(xù)使用,降低結(jié)構(gòu)功能中斷時(shí)間以實(shí)現(xiàn)震后可恢復(fù)功能的更高目標(biāo)。為達(dá)到上述目標(biāo),Pettinga等[1]將彈性框架作為恢復(fù)力機(jī)制與主結(jié)構(gòu)組成復(fù)合體系,既可以降低結(jié)構(gòu)的殘余位移又可以增加結(jié)構(gòu)抵抗地震作用的能力;Terán-Gilmore等[2]將彈性抗彎框架與帶有屈曲約束支撐(Buckling-Restrained Brace, BRB)的框架組合,利用彈性框架作為自復(fù)位機(jī)制消除由于BRB屈服引起的殘余位移取得了較好的控制效果。由此可見(jiàn)利用彈性框架作為實(shí)現(xiàn)自復(fù)位的策略可以有效地降低結(jié)構(gòu)的殘余位移,避免了使用預(yù)應(yīng)力或者后張拉裝置帶來(lái)的施工和維護(hù)上的復(fù)雜性;并且這種雙抗力的復(fù)合結(jié)構(gòu)體系可以提高結(jié)構(gòu)的冗余度和魯棒性(稱之為復(fù)合I型)。
與附加底部與基礎(chǔ)固接的彈性框架組成復(fù)合體系不同,MacRae等[3]研究發(fā)現(xiàn)鋼框架結(jié)構(gòu)中的搖擺重力柱可以有效降低結(jié)構(gòu)在地震作用下的層間位移集中現(xiàn)象,降低結(jié)構(gòu)出現(xiàn)局部薄弱層破壞的可能性。將底部與基礎(chǔ)鉸接的附加搖擺機(jī)構(gòu)與主結(jié)構(gòu)組合成復(fù)合體系,利用附加的搖擺體約束主結(jié)構(gòu)的變形模式,使得主結(jié)構(gòu)的層間位移角在地震作用下產(chǎn)生重分布,降低層間位移角的局部集中程度,避免因局部損傷過(guò)于嚴(yán)重而導(dǎo)致結(jié)構(gòu)整體失效(稱之為復(fù)合Ⅱ型)。曲哲等[4]將搖擺墻、金屬阻尼器與框架結(jié)構(gòu)組合使用,不僅降低了結(jié)構(gòu)的響應(yīng)而且使得結(jié)構(gòu)的層間位移角分布趨于均勻;吳守君等[5]分析了框架-搖擺墻結(jié)構(gòu)的受力特點(diǎn),提出了搖擺墻加固的具體方法以及連接的局部構(gòu)造。Qu等[6]將底部鉸接的Rocking Cores與中心支撐鋼框架(Concentrically Braced Frames, CBFs)組合在一起,利用Rocking Cores限制CBFs的層間位移集中程度。因此利用底部與基礎(chǔ)鉸接的搖擺體可以有效地控制結(jié)構(gòu)的層間位移集中程度,降低結(jié)構(gòu)局部的位移需求,避免因局部過(guò)度損傷而使結(jié)構(gòu)退出工作。
根據(jù)上述分析可以發(fā)現(xiàn),底部固結(jié)的彈性框架可以作為自復(fù)位機(jī)制降低主結(jié)構(gòu)的殘余位移,而底部鉸接的搖擺墻或者搖擺框架可以通過(guò)層間位移的重分布限制結(jié)構(gòu)的局部層間位移集中程度。為將復(fù)合體系的這兩個(gè)機(jī)制集成到一個(gè)體系中,杜永峰和武大洋[7]提出一種新型復(fù)合體系,RC框架-自復(fù)位消能搖擺剛架。與上述文獻(xiàn)中體系不同,自復(fù)位消能搖擺剛架與基礎(chǔ)的連接為彈性轉(zhuǎn)動(dòng)約束,通過(guò)底部?jī)蓚€(gè)耦合的自復(fù)位阻尼器實(shí)現(xiàn)可更換的耗能機(jī)制,既可以消除殘余位移又可以限制結(jié)構(gòu)的層間位移集中,是一種效率較高的復(fù)合體系。本文以上述研究[7-8]為基礎(chǔ),將RC框架拓展為一般的框架結(jié)構(gòu)體系,與自復(fù)位消能搖擺剛架組成復(fù)合自復(fù)位結(jié)構(gòu)體系(稱之為復(fù)合Ⅲ型)。
復(fù)合體系的設(shè)計(jì)及其限制層間位移集中程度的評(píng)估,需要將體系的變形模式引入到性能指標(biāo)中,而傳統(tǒng)的基于單自由度體系的反應(yīng)譜給出的是結(jié)構(gòu)整體的反應(yīng)指標(biāo),無(wú)法反映結(jié)構(gòu)沿高度的層間位移角的變化趨勢(shì)。再者,單自由度體系的反應(yīng)譜也無(wú)法反映高階模態(tài)對(duì)體系層間位移角需求的影響[9-10]。為克服反應(yīng)譜的以上缺陷,Iwan[9]在1997年提出了量化體系位移角需求的指標(biāo):層間位移角譜(Interstory Drift Spectrum, IDS)。與傳統(tǒng)的基于單自由度體系的反應(yīng)譜不同,IDS是以連續(xù)剪切梁為數(shù)值模型,該模型最大的優(yōu)點(diǎn)是可以將體系層間位移角沿高度的分布考慮其中,通過(guò)多模態(tài)的疊加考慮高階振型對(duì)體系層間位移角的影響,可以更加準(zhǔn)確地計(jì)算體系的最大層間位移角需求。Miranda和Akkar[10]將Iwan[9]提出的以連續(xù)剪切梁為模型的IDS拓展為廣義層間位移角譜(Generalized Interstory Drift Spectrum, GIDS)。GIDS將連續(xù)剪切梁模型拓展為由剪切梁和彎曲梁組成的復(fù)合體系模型,通過(guò)改變剪切梁和彎曲梁之間的剛度比,該模型可以用來(lái)分析多種結(jié)構(gòu)體系,包括剪切變形為主的結(jié)構(gòu)、彎剪變形的結(jié)構(gòu)和彎曲變形為主的結(jié)構(gòu)。楊迪雄等[11]基于Miranda和Akkar[10]的成果,利用GIDS研究了彎剪型結(jié)構(gòu)在近場(chǎng)脈沖型地震作用下層間位移沿結(jié)構(gòu)高度分布的規(guī)律,證明GIDS可以有效反映體系的變形規(guī)律,為設(shè)計(jì)和評(píng)估體系提供一定的參考。
本文將復(fù)合自復(fù)位結(jié)構(gòu)體系中的框架結(jié)構(gòu)簡(jiǎn)化為底部固接的剪切懸臂梁,將自復(fù)位消能搖擺剛架簡(jiǎn)化為底部彈性約束的彎曲梁,由二者組成復(fù)合體系理論模型。通過(guò)求解該復(fù)合體系理論模型得到體系振型的閉合解,進(jìn)而可以得到體系的GIDS。以剪切梁和彎曲梁剛度比、彎曲梁與基礎(chǔ)轉(zhuǎn)動(dòng)彈簧的剛度比為參數(shù),分析了復(fù)合體系在不同剛度比下的振型和振型轉(zhuǎn)角的變化規(guī)律,以及復(fù)合自復(fù)位結(jié)構(gòu)體系的層間位移角譜在兩種剛度比、阻尼比和高階振型下的變化規(guī)律。

