基于最優線性無偏預測任意協方差下估計錯誤發現率

王湘玉，張寶學，齊春香

（1.河北科技師范學院 工商管理學院，河北 秦皇島 066004；2.首都經濟貿易大學 統計學院，北京 100070；3.東北師范大學 數學與統計學院，長春 130024）

0 引言

多重假設檢驗是高維統計推斷的基本問題，也是目前統計研究的熱點問題之一，應用的領域非常廣泛。比如，在金融學中，需要對數以萬計的原假設同時進行檢驗，用以確定哪個客戶經理的能力更強。再如，在全基因組相關性研究中，希望在大量的基因數據中找到與某性狀或疾病相關的SNP位點，同樣需要同時對數以萬計的原假設進行檢驗。而在進行多重假設檢驗的過程中，一個非常重要的問題，就是如何更好地控制總體的錯誤率。

Benjamini和Hochberg(1995)[1]提出了多重假設檢驗的FDR標準(E[V/R],即在m個原假設中，錯誤拒絕的原假設個數V占拒絕的原假設個數R的比例的期望)。之后，Storey(2002)[2]、Efron(2010)[3]等眾多學者對FDR進行了更為深入的研究。然而大部分的研究往往都是基于原假設相互獨立為前提。但是這種假設往往較為嚴苛，很難達到。因為實際問題中的原假設通常具有某種相關性。舉例來說，如果某個原假設是顯著的，那么在它附近的其他原假設就有更大的可能性也是顯著的。

也有一些學者針對原假設相關的情況做了一些研究，比如Benjamini和Yekutieli（2001）[4]在正回歸相依情況下研究了FDR的估計問題。再如，Storey等（2004）[5]在弱相關情況下估計FDR。但是這些相關關系都過于特殊，急需找到一種在原假設的任意相關情況下的FDR估計方法。

Fan等（2012）[6]提出了一種任意協方差結構下的FDP(False Discovery Proportion，即V/R)估計方法。然而在估計隨機變量W時，將其當作參數，采用L1估計方法。實際上，所得的模型是一個混合效應模型，對此，本文基于最優線性無偏預測方法，估計隨機變量W，進而提出一種新的FDP估計方法，最終估計FDR。

1 最優線性無偏預測

最優線性無偏預測[7]是針對混合效應模型，估計隨機變量的一種方法。對于混合效應模型y=Xβ+Zu+ε,其中y是有N個觀測的向量；X是N×p的已知矩陣；β是p×1的未知向量（p個未知常數），看作固定效應部分；Z是N×q的已知矩陣；u是q×1的隨機向量，看作隨機效應部分；ε是隨機誤差項，是N×1的隨機向量。

顯然有 E(u)=0,E(ε)=0 ，定義：

Var(u)=D'Var(ε)=R'Cov(u'ε')=0

因此，V=Var(y)=Var(Zu+ε)=ZDZ'+R

Henderson(1950)[8]得到β和u的最優線性無偏預測：

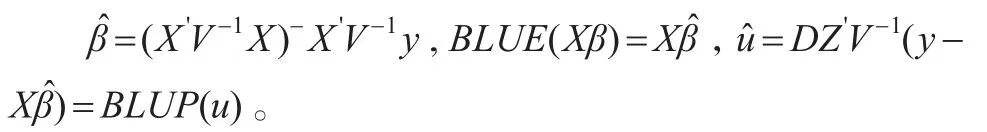
由公式[9]可得：

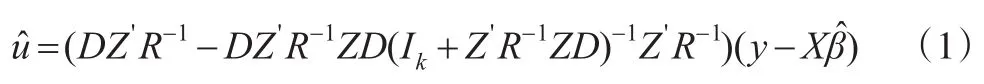
2 基于最優線性無偏預測估計FDP

2.1 理論分析

定義由n個樣本構成的第j個SNP位點的基因型數據為個樣本的表現型數據為Y=(Y1' …'Yn)T。現考慮和的邊際線性回歸可以得到βj的最小二乘估計。

這樣可以同時檢驗p個假設：

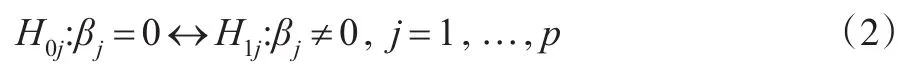
其中，原假設表示第j個SNP位點與性狀無關。

將標準化，記為 Z1'…'Zp，則有其中是 X 相關系數矩陣，∑的第(k ' l)個元素為rkl，對角元素為1。

因此，檢驗問題（2）等價于：

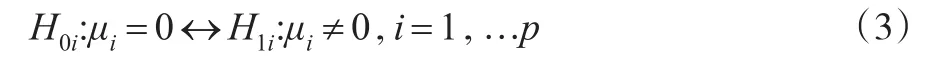
通過對∑進行特征分解，得出其中 λ1≥…≥λp是 ∑ 的p個特征值，γ1'…'γp是對應的p個特征向量，那么這樣 Zi可被分解成：

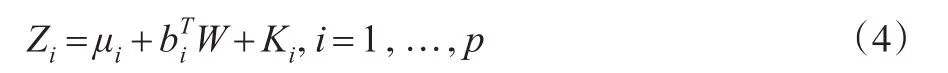
其中k。W1'…'Wk相互獨立，且與K1'…'Kp獨立。W=(W1…,

對于混合效應模型（4），當 y=Z'X=0'Z=L'u=W'D=Ik'R=A時，帶入式（1）可得：

針對混合效應模型（4），取前75%p(記為m)個最小的對應m個最小的 | μi|，并且將L的分量對應排序后，取前m行,從而對應有的形式，取A=A11,這樣可以將這些 ||Zi看成是在原假設式（6）下：

其中Z是有m個觀測值的m×1向量是m×k矩陣；W 是k×1隨機向量，是隨機效應部分；K是m×1隨機向量，是隨機誤差項。并且有，V=Var(Z)=∑=Var(LW+K)=LL'+A。

Tipping和Bishop(1999)[10]基于高斯潛在變量角度提出下述概率模型，此模型體現了主成分分析的思想：

其中

在原假設下，

因此，將模型（6）替代為模型（7），有：

進而由式（5）可得到W 的估計為：

下面估計σ2，Z的密度函數是：

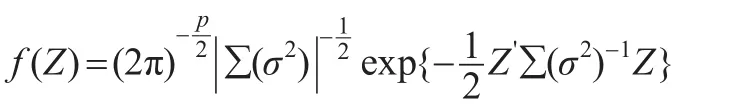
似然函數為：

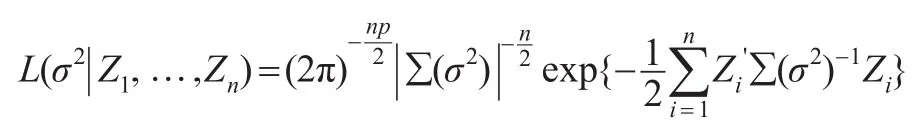
對數似然函數為：

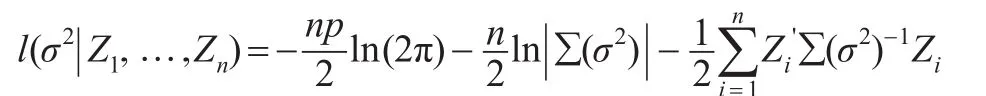
由得到：

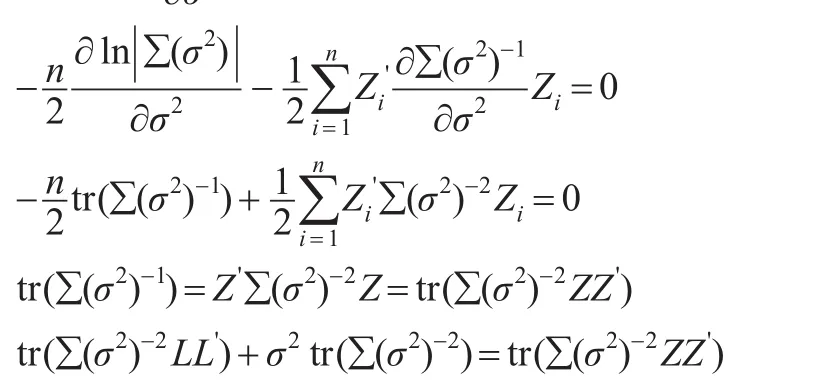
從而得到：

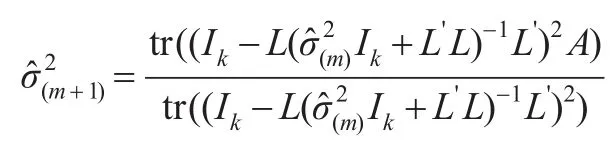
最終可以估計σ2，帶入式（8）中得出：

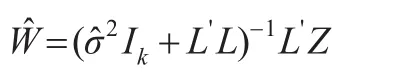
這時，可以得出任意協方差結構下的FDP估計：

其中是標準正態分布的累積分布函數是標準正態下的分位數，ηi的估計記為。

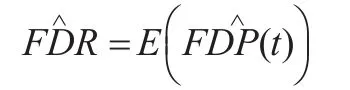
2.2 模擬及結果

檢驗統計量現考慮以下六種模型下的協方差陣結構。其中，Xi產生過程分別如下：

（1）等相關模型其中 ∑為對角元素是1，其余元素是1/2的矩陣。

（2）Fan和Song[6]的模型令N(0'1)，且：

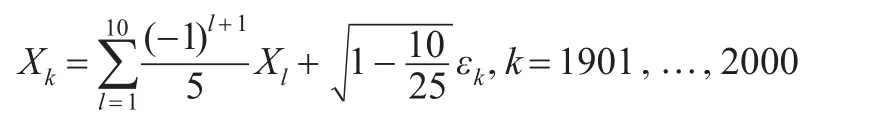
其中

（3）獨立柯西模型：對于是獨立同分布的柯西分布的隨機變量，其中x0=0'γ=1。

（4）三因子模型：對于 X=(X1'…,Xp)，取 Xj=ρ(1)Wj(1)其 中

（5）雙因子模型：對于 X=(X1'…'Xp)，取其中

（6）非線性因子模型：對于取

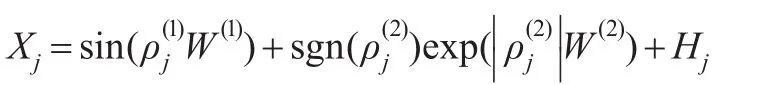
其中

令SNP位點個數 p=1000,n=100'σ=2,錯誤的原假設個數 p1=50，原假設下 β0=0，備擇假設下 β1=1，做1000次模擬。上述六種相關模型下的FDP估計值與真值比較結果如圖1所示。

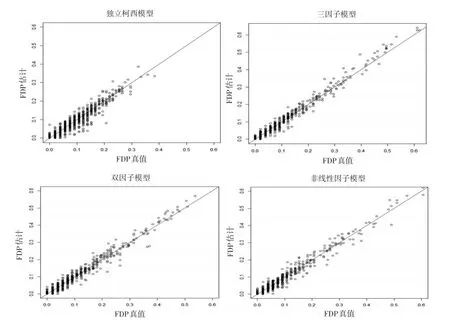
圖1

圖2為六種模型的FDP估計值與真值的相對誤差(即

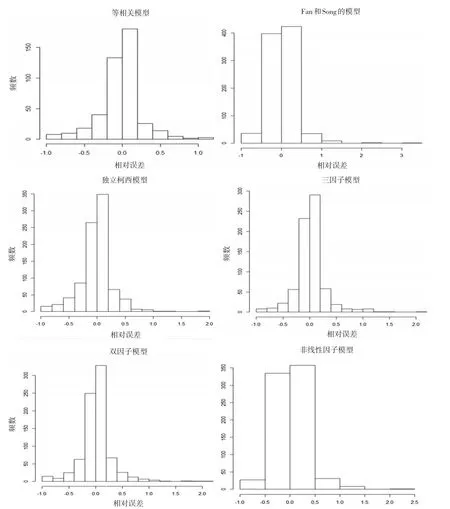
圖2

從模擬結果可以看出，本文給出的FDP估計值在真值附近波動，理論上合理。

3 結論

多重假設檢驗是高維統計推斷的基本問題，也是目前統計研究的熱點問題之一，應用領域十分廣泛。比如，金融領域內，要得知哪個客戶經理的能力更強。再如，全基因組相關性的研究中，要在大量的基因數據中尋找與性狀或疾病相關的SNP位點，往往都需要同時對數以萬計的假設進行檢驗。而在進行多重假設檢驗問題時，往往需要控制總體錯誤率FDR。棘手的是，實際問題中的原假設往往具有一定相關性。對此，本文提出一種新的估計FDR的方法，即在檢驗統計量的任意協方差結構下，對混合效應模型使用最優線性無偏預測方法估計隨機變量W，從而估計FDP，進而估計FDR。模擬表明，本文給出的FDP估計值在真值附近波動，理論上比較合理。

但是由于采用最優線性無偏預測的方法，估計FDP在運算速度上不夠快捷，還有待在今后的研究中進一步地完善。

[1]Benjamini Y，Hochberg Y.Controlling the False Discovery Rate:A Practical and Powerful Approach to Multiple Testing[J].Journal of the Royal Statistical Society,SeriesB,1995,(57).

[2]Storey J D.,A Direct Approach to False Discovery Rates[J].Journal of the Royal Statistical Society,2002.

[3]Efron B.Correlated Z-Values and the Accuracy of Large-Scale Statistical Estimates[J].Journal of the American Statistical Association,2010,(105).

[4]Benjamini Y，Yekutieli D.The Control of the False Discovery Rate in Multiple Testing Under Dependency[J].The Annals of Statistics,2001,(29).

[5]Storey J D，Taylor J E，Siegmund D.Strong Control,Conservative Point Estimation and Simultaneous Conservative Consistency of False Discovery Rates:A Unified Approach[J].Journal of the Royal Statistical Society,2004,(66).

[6]Fan J,Han X,Gu W.Estimating False Discovery Proportion Under Arbitrary Covariance Dependence[J].Journal of the American Statistical Association,2012.

[7]王松桂，史建紅，尹素菊，吳密霞.線性模型引論[M].北京：科學出版社,2004.

[8]Henderson C R.Estimation of Genetic Parameters[J].Ann.Math.Statist.,1950,(21).

[9]Benameur S,Mignotte M,Destrempes F,et al.Estimation of Mixtures of Probabilistic PCA with Stochastic EM for the 3D Biplanar Reconstruction of Scoliotic Rib Cage[J].Image Processing,2004,(5).

[10]Tipping M E,Bishop C M.Probabilistic Principal Component Analysis[J].Journal of the Royal Statistical Society,1999.