平滑轉移自回歸模型及其應用

李 娜，鄭少智

（暨南大學 經濟學院，廣州 510632）

0 引言

股票市場作為市場經濟的一個重要組成部分，對國民經濟的發展有著非常重大的作用，股票市場的繁榮和穩定是國民經濟的“晴雨表”，所以，有許多的經濟學家和實際工作者對股票市場進行了深入地研究，結果發現，對于常用的股票模型，比如：AR模型、ARCH模型以及ARIMA模型等并不能很好地刻畫出股票的市場行為，但隨著非線性時間序列分析的近二十年的發展，其在經濟、金融等領域有著廣泛的應用前景，這些非線性模型能夠更好地模擬實際經濟和金融中的數據。對于平滑轉換自回歸（STAR）模型，常用的兩種模型有：邏輯斯蒂平滑自回歸（LSTAR）模型和指數平滑自回歸（ESTAR）模型，這兩種模型分別是以邏輯斯蒂函數和指數函數作為平滑函數來建立STAR模型，本文采用是高斯核函數作為平滑函數來建立STAR模型，并將該模型用于股票市場特性的研究中，通過實證研究結果表明，該模型能夠很好地刻畫出股票的市場行為。

1 STAR模型的建立

1.1 模型的描述

STAR模型由Granger和Ter?svirta于1993年提出以來，目前已經形成了一套比較成熟的建模程序，包括平滑轉換自回歸模型（STAR）的設定與估計以及如何確定平滑函數等。一個二制度的STAR模型的一般表達式為：

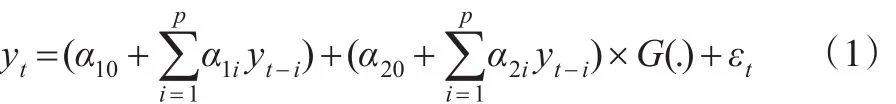
其中，yt是研究的時間序列，α10、α20是常數，p是所研究時間序列的滯后階數，εt是獨立同分布的隨機變量，G(.)是一個連續的平滑函數，取值范圍為[0,1]，它決定了兩個制度之間相互轉換的方式，當 G(.)=0時，yt是一個AR(P)過程；當 G(.)=1時，yt是一個兩機制混合的AR(P)過程；當0＜G(.)＜1時，yt在兩機制之間平滑的轉換，而轉換的方式由G(.)的具體函數形式決定。G(.)可以是連續的奇函數或偶函數，例如G(.)可以是滿足G(-∞)=0與G(+∞)=1的單調遞增的奇函數，也可以是滿足G(±∞)=0 與G(0)=1的偶函數，比如正態分布 N(μ'σ2)的累積分布函數和正態分布N(μ'σ2)的密度函數都可以作為平滑函數來建立平滑轉換自回歸模型。

對于平滑函數G(.)，目前常用的兩種平滑函數包括邏輯斯蒂函數和指數函數，其中，邏輯斯蒂函數的具體表達式如下：

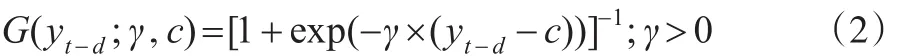
其中，yt-d是門限變量，d是延遲參數，c是兩個機制之間的門限值，若平滑函數 G(.)設定為這種邏輯斯蒂函數形式，則式（1）被稱為邏輯斯蒂平滑自回歸模型，即LSTAR模型。

隨著 yt-d的增加，邏輯斯蒂函數 G(yt-d;γ'c)從0到1單調遞增，轉換參數γ的大小決定了該函數的平滑性，即決定了機制轉換的速度，假如轉換參數γ的值很大，那么門限變量yt-d相對于門限值c的很小的變化都會導致機制間的劇烈轉換。當γ→+∞時，函數G(yt-d;γ'c)從0到1的變化幾乎是瞬時的，此時有G(yt-d;γ'c)=I(yt-d＞c)，在這種情況下，LSTAR模型變為SETAR模型；當γ→0時，G(yt-d;γ'c)=0.5，此時的LSTAR模型變為線性AR模型。

另一種平滑函數是指數函數，其具體表達式如下：

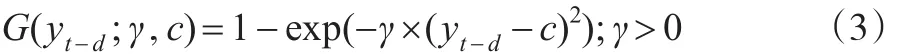
其中，yt-d是門限變量，d是延遲參數，c是門限值，若平滑函數G(.)設定為這種指數函數形式，則式（1）被稱為指數平滑自回歸模型，即ESTAR模型。

隨著 yt-d趨于c值，函數G(yt-d;γ'c)趨于0；隨著yt-d遠離c值，G(yt-d;γ'c)趨于1。經過研究表明，ESTAR模型比較適合時間序列出現拐點的情況。當γ→+∞時，G(yt-d;γ'c)=1，當γ→0時，G(yt-d;γ'c)=0，所以，不論是γ→+∞還是γ→0，ESTAR模型都退化為線性AR模型。

1.2 STAR模型的估計

在估計STAR模型之前，首先需要對時間序列的平穩性進行檢驗，因為在一般情況下，未經處理的金融數據都是非平穩的，如果直接對非平穩的時間序列進行回歸分析，那么就會造成偽回歸問題，所以，在進行模型的估計之前首先需要對數據進行平穩性檢驗，如果數據非平穩，那么就要對數據進行處理使其平穩，比如進行一階差分，或者用對數收益率數據等。

STAR模型的估計由以下三個步驟組成。

（1）確定線性AR模型。可以根據Ljung-Box統計量來檢驗殘差的自相關性，在殘差序列不存在自相關的條件下，可以根據Akaike information criterion(AIC)來選擇線性AR模型的最大滯后階數P。

（2）依據延遲參數d的不同取值進行線性檢驗，拒絕線性檢驗的同時，也確定d的取值。一般情況下，d的取值是1≤d≤p的正整數，也可以根據實際情況適當的調整d的取值范圍。當d取不同的值時，分別進行線性性檢驗，H0：線性AR模型成立；H1：STAR模型成立。因為非線性模型中有線性模型不存在的參數，所以不能直接進行檢驗，Luukkonen等（1988）提出，可以將平滑函數G(.)在γ=0時用三階泰勒公式展開，由此得出以下回歸模型：

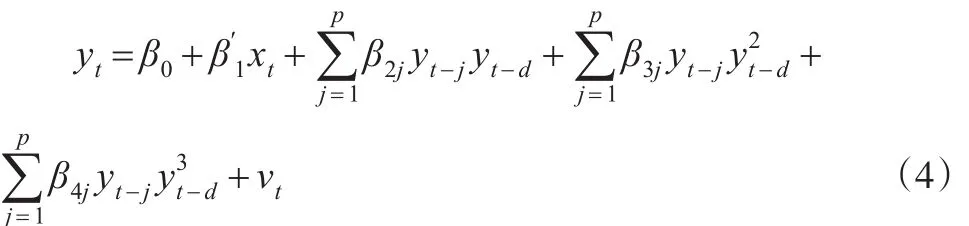
其中是誤差項。

原假設為：

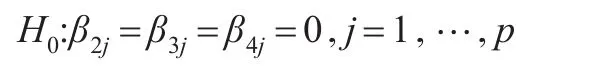
對式（4）進行LM檢驗，當所用數據為小樣本時，LM統計量服從F分布，LM統計量在大樣本情況下漸進服從卡方分布，計算出LM統計量的值和P值，如果有多個d值相對應的上式拒絕線性原假設，那么就應選擇最小的P值所對應的d的取值。

（3）利用嵌套假設的序貫檢驗對LSTAR模型和ESTAR模型進行選擇。d值確定以后，需要檢驗的序貫假設是：

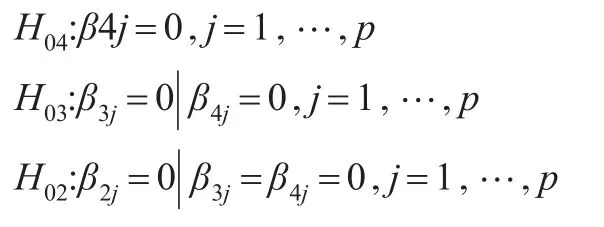
若拒絕H04，則選擇LSTAR模型；若接受H04而拒絕H03，則選擇ESTAR模型；若接受H04和H03而拒絕H02，則選擇LSTAR模型。

Granger和Ter?svirta（1993），Ter?svirta（1994）提出，嚴格按照以上序貫檢驗的步驟對LSTAR模型和ESTAR模型進行選擇也有可能得出錯誤的結論，所以他們認為可以計算出上述三個假設的所有LM檢驗的P值，若H03的P值最小，那么就選擇ESTAR模型；否則，就應選擇LSTAR模型。

選擇好具體的模型之后，再對模型進行非線性最小二乘估計，求出模型參數的估計值，并對殘差進行Ljung-Box自相關性檢驗和ARCH異方差性的檢驗，目的在于檢驗所建立的模型是否充分適當。

2 基于非參數平滑的STAR模型

根據前文所述，平滑轉換自回歸（STAR）模型在制度間的轉換是連續平滑的，轉換方式取決于所選取的平滑函數，常用的兩種平滑函數為邏輯斯蒂函數和指數函數。隨著非參數平滑技術的逐漸成熟，其在很多領域都有廣泛的應用，所以本文用基于非參數平滑的方法去建立STAR模型，即選擇核函數為平滑函數來建立STAR模型，然后再對模型進行估計。其具體的表達式為：

其中，Kh(.)=K(./h)/h，h為非參數平滑的帶寬或者叫平滑參數，yt-d為門限變量，c為門限值。核密度函數K(.)在(-∞'+∞)上滿足以下條件：

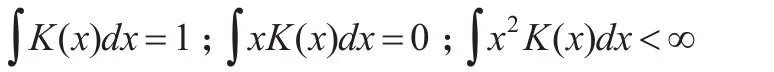
其中，帶寬h也需滿足：

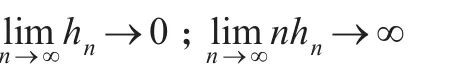
常用的核函數包括高斯核函數和對稱貝塔(Beta)族：

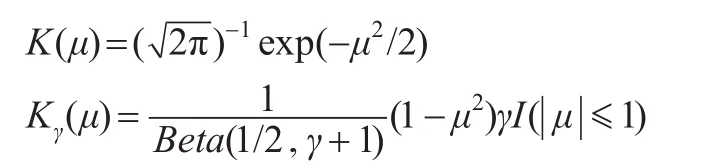
當γ=0'1'2和3時，分別對應于均勻核函數、Epanechnikov核函數、雙權（Biweight）核函數和三權（Triangle）核函數。

在非參數平滑技術中，一個核平滑性能的優劣，取決于核函數和平滑參數h的選取。范劍青和姚琦偉在其所著的《非線性時間序列》一書中指出，無論是從經驗的角度還是從理論的角度，核函數的選擇并不是太重要，只要所選的核函數是對稱的和單峰的，并且當平滑參數h的選擇是最優時，核函數的選擇對非參數平滑的優劣性幾乎沒有影響。平滑參數h是控制平滑精度的主要參數，太大的h會使得平滑過度，太小的h會導致平滑不足，所以選擇一個最優的平滑參數h至關重要。

根據研究表明，對最優平滑參數的選取，可以用最小化MISE（mean integrated square error）的方法，得出漸近最優平滑參數，下面給出正態參考帶寬選擇：

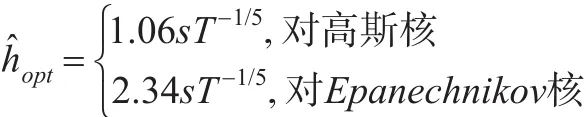
其中s是樣本標準差，T是樣本數量。正態參考帶寬選擇在數據近似為高斯分布時，它是一個很好的平滑參數的選取方法，而且根據許多的實際應用的結果表明，這種選擇方法是合理的，然而，正態參考帶寬選擇只是一個簡單的經驗方法，當數據的真實分布是非對稱的或者是多峰時，它就有可能導致平滑過渡，在這種情況下就需要主觀地調整h，或者用更精細的方法來選擇最優的平滑參數。

另外一種常見的最優平滑參數的選擇方法是交叉驗證法（cross-validation,簡記為CV），其基本思想是，去掉第i個觀測值，得到m(x)的具有平滑參數h的缺一估計：

使用上述估計量，得出缺一交叉驗證得分：

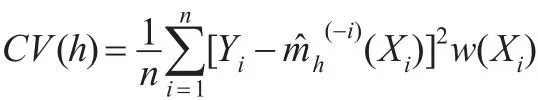
其中w(x)為非負的權因子函數，在一維的情況下可取w(x)=I( ||x-0.5≤0.4)

自動最優平滑參數定義如下：

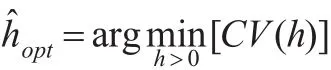
3 實證分析

3.1 數據與平穩性檢驗

本文選取了中航地產從2013年7月10日至2014年9月5日的共286個日收盤價數據進行實證分析，數據來源于Wind資訊。下面給出日收盤價數據的時間序列圖，見圖1。

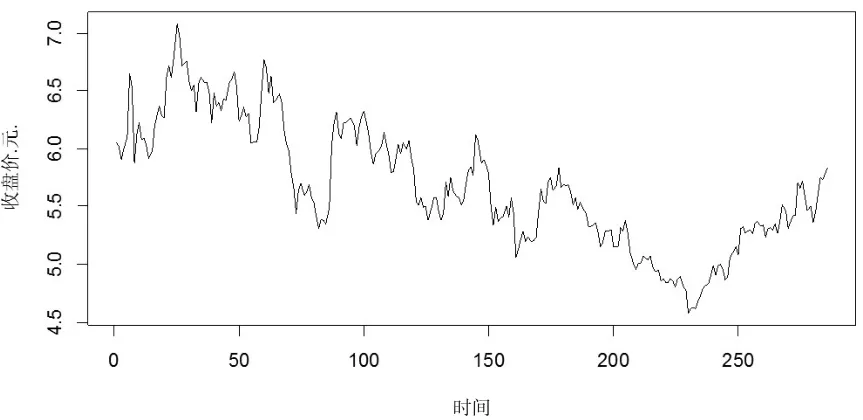
圖1 中航地產日收盤價數據

根據前文所述，在建立模型之前需要對數據進行平穩性檢驗，所以本文用增廣的迪基-富勒檢驗來檢測該時間序列的平穩性，其檢驗結果如表1所示：

表1 變量的平穩性檢驗結果

檢驗結果由R軟件編程計算得出，在該檢驗中，原假設H0為時間序列非平穩，備擇假設H1為平穩，根據表1，計算的P值為0.4142，所以在5%水平下不能拒絕原假設，說明中航地產的日收盤價數據是非平穩的，為進一步分析，必須要對數據進行處理使其通過平穩性檢驗，所以本文選擇用對數收益率數據來進行分析，圖2為中航地產的對數收益率數據的時間序列圖。

圖2 中航地產日對數收益率數據

再對日對數收益率數據進行單位根檢驗，檢驗結果如表2所示：

表2 變量的平穩性檢驗結果

根據表2的檢驗結果，P值為0.01，所以在5%的水平下拒絕原假設，即該對數收益率數據具有整體平穩性。

3.2 線性性檢驗、STAR模型的設定與估計

本文實證分析部分的主要步驟為：（1）確定線性AR模型的最大滯后階數P；（2）進行線性性檢驗并確定延遲參數d；（3）對模型參數進行估計；（4）對模型殘差進行檢驗。

根據Granger和Ter?svirta（1993）的建議，可以根據偏自相關圖和AIC準則或SC準則來確定最大滯后值P，由此，本文確定最大滯后階數P為5。

接下來進行線性性檢驗并確定延遲參數d的值，d的取值范圍為1≤d≤5的正整數，所以對每個d值，分別進行線性檢測，并計算出相應的P值，結果如表3所示：

表3 線性性檢驗結果

根據表3的檢驗結果，在5%的水平下，當d取值為2和4時拒絕線性性假設，在這種情況下應取最小的P值所對應的d的取值，所以，延遲參數d=2。

在用非參數平滑建立STAR模型時，需要對核函數和平滑參數進行選擇，本文選用高斯核函數作為平滑函數，并用交叉驗證法（CV）計算出平滑參數h，再對STAR模型進行非線性最小二乘估計，得出STAR模型為：

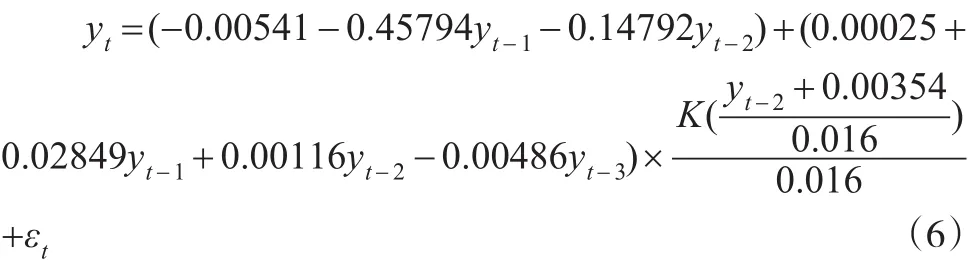
其中，門限值為-0.00354，平滑參數h為0.016，核函數K(.)為高斯核函數，即：

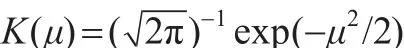
在平滑函數中位置參數d=2，說明制度轉換的發生取決于自身滯后的第二期，門限值為-0.00354，表明對數收益率在-0.00354時正處于下降與上升的中間狀態。

接下來需要對擬合的模型進行診斷檢驗，本文選擇對模型殘差分別進行Ljung-Box自相關性檢驗和ARCH異方差性的檢驗，若檢驗結果表明模型殘差不存在自相關性也不存在異方差性，則說明擬合的模型是充分適當的，檢驗結果如表4所示：

表4 模型診斷檢驗結果

由表4的檢驗結果可知，在5%的顯著水平下，Ljung-Box檢驗和ARCH檢驗都能通過，模型殘差不存在自相關，也不存在異方差，表明上述模型能很好地刻畫出股票的市場行為。

接下來將該模型與線性AR模型、LSTAR模型和ESTAR模型進行一個簡單的對比，分別對各個模型擬合的殘差進行檢驗，檢驗結果如表5所示：

表5 模型殘差檢驗結果

表5為上述三個模型殘差的自相關性和異方差性檢驗的P值，在5%的顯著水平下，AR模型的殘差無法通過滯后六期的異方差性檢驗，其他的檢驗都能通過，但與表4結果相比，AR模型、LSTAR模型和ESTAR模型的殘差檢驗結果都不如基于非參數平滑的STAR模型顯著，也就是說，以核函數為平滑函數的擬合效果比其他模型的效果要好。并且S/SL=0.97063，S SL是非參數平滑模型回歸的標準誤差與AR模型回歸的標準誤差的比值，其值小于1，說明該模型優于線性AR模型。

時間序列模型的建立，其中一個很重要的應用就是預測，所以一個模型的優劣也可以根據預測的表現來判斷，當一個模型能比其他的模型更好地預測時間序列的未來走勢時，那么就說明在某些程度上該模型比其他模型更好，所以接下來本文再對模型的預測方面進行一個簡單的對比。本文采用誤差均方根（root-mean-square error,簡記為RMSE）作為評價預測效果的標準，RMSE越小的模型則越好。

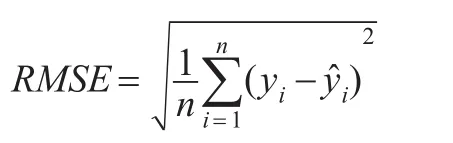
基于非參數平滑的STAR模型的RMSE值為0.0215，與表6中的其他模型的RMSE值相比，該模型的RMSE值最小，也就是說，該模型在預測方面也優于線性AR模型、LSTAR模型和ESTAR模型。

表6 模型預測評價值

根據本文的研究，無論是在樣本擬合方面，還是預測方面，基于非參數平滑的STAR模型要優于其他模型，尤其是線性模型，所以可以得出股票市場具有非線性特性的結論。

4 結論

我國股票市場的經濟環境復雜，使得單一傳統的線性模型無法很好地刻畫出股票的市場行為，本文首次用非參數平滑的方法建立STAR模型，并將該模型用于我國股票市場動態行為的研究中，通過實證研究表明股票市場的非線性特征，并證實了用高斯核函數來代替邏輯斯蒂函數和指數函數作為平滑函數來建立STAR模型是充分適當的，模型殘差能夠通過一系列檢驗，并且在該研究中，非參數平滑的STAR模型的預測效果也優于線性AR模型、LSTAR模型和ESTAR模型，由此表明，基于非參數平滑的STAR模型用于研究我國股票市場行為非常有效。

[1]Granger C W J,Ter?svirta T.Modeling Nonlinear Economic Relationships[M].Oxford:Oxford University Press,1993.

[2]Ter?svirta T.Specification,Estimation,and Evaluation of Smooth Transition Autoregressive Models[J].Journal of the American Statistical Association,1994,89(425).

[3]Tong H.Threshold Models in Nonlinear Time Series Analysis[M].New York:Springer Verlag,1983.

[4]Fan J Q,Yao Q W.Nonlinear Time Series:Nonparametric and Parametric Methods[M].Beijing:Science Press,2006.

[5]Seo M H,Linton O.A Smoothed Least Squares Estimator for Threshold Regression Models[J].Journal of Econometrics,2007,141(2).

[6]McMillan D G.Nonlinear Predictability of Stock Market Returns:Evidence From Nonparametric and Threshold Models[J].International Review of Economics and Finance,2001,10(4).

[7]Switzer L N,Picard A.Stock Market Liquidity and Economic Cycles:A Non-linear Approach[J].Economic Modelling,2016,(57).

[8]克萊夫·W.J.格蘭杰，蒂莫·泰雷斯維爾塔.非線性經濟的建模[M].上海:上海財經大學出版社,2006.

[9]王俊，孔令夷.非線性時間序列分析STAR模型及其在經濟學中的應用[J].數量經濟技術經濟研究，2006,(1).

[10]薛留根.應用非參數統計[M].北京：科學出版社,2013.

[11]范劍青，姚琦偉.非線性時間序列——建模、預報及應用[M].北京:高等教育出版社,2005.

[12]王斌會.計量經濟學模型及R語言應用[M].廣州:暨南大學出版社,2015.

[13]謝赤，戴克維，劉潭秋.基于STAR模型的人民幣實際匯率行為的描述[J].金融研究，2005,（5）.

[14]劉宇.我國股票市場的非線性研究——基于LSTAR模型[J].管理工程學報，2008，22（1）.

[15]靳曉婷，張曉峒，欒惠德.匯改后人民幣匯率波動的非線性特征研究——基于門限自回歸TAR模型[J].財經研究，2008,34（9）.