相依保險風(fēng)險的非參數(shù)估計

孫 榮

（重慶工商大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院，重慶 400067）

0 引言

對于風(fēng)險定價,信度理論是一種重要的經(jīng)驗定價方法。信度理論產(chǎn)生于20世紀(jì)20年代，至今已有90多年的歷史，在非壽險精算理論與實務(wù)中具有重要地位，精算師根據(jù)過去的單個風(fēng)險或者一個保單組合風(fēng)險的經(jīng)驗數(shù)據(jù)，調(diào)整未來的保險費。信度理論的研究主要形成了兩個不同的分支：（1）建立在頻率方法上的有限擾動理論；（2）以貝葉斯理論為基礎(chǔ)的最精確一可信度理論。這兩種方法都是希望通過已有的歷史數(shù)據(jù)來合理地制定保費。

在已有的風(fēng)險理論中,個體風(fēng)險常常假設(shè)是相互獨立的,主要是因為獨立假定比具有一定相關(guān)性的假定在數(shù)學(xué)的處理上更容易一些。Li（2000）[1],Cheng（2003）等[2]研究了保險風(fēng)險獨立同分布的情況下保費與風(fēng)險載荷非參數(shù)估計量的弱、強收斂性與漸進(jìn)正態(tài)性，但在保險實踐中，在很多情況下，個體風(fēng)險由于它們有相同的索賠產(chǎn)生機制或是由于共同的經(jīng)濟和物理環(huán)境的影響，表現(xiàn)出一定的相關(guān)性，因此，對相依結(jié)構(gòu)下保險風(fēng)險的非參數(shù)估計研究具有更為重要的理論價值和現(xiàn)實意義。本文在保險風(fēng)險具有強混合特點的相依結(jié)構(gòu)前提下，提出了基于PH變換與條件尾期望原理的保費與風(fēng)險載荷的非參數(shù)估計量，分析了相關(guān)估計量的強收斂性與漸近正態(tài)性。除了少數(shù)異常值情況外，蒙特卡洛的實證證據(jù)顯示了它們良好的估計精度。

1 主要結(jié)論與定理

在精算科學(xué)中，保險風(fēng)險X常常界定為一個非負(fù)的隨機變量，其相對應(yīng)的保費是保險風(fēng)險的一個函數(shù)：H(X):X→[0 ' ∞ )。假設(shè)F為保險風(fēng)險X的分布函數(shù)，定義S=1-F.Wang[3-5]將PH-變換保費定義為：

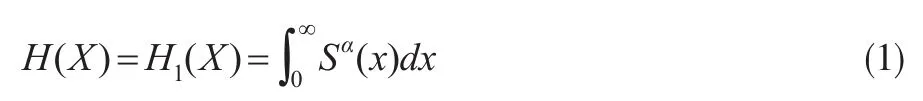
其中α∈(0 ' 1)是一個常數(shù)。假設(shè)保險風(fēng)險X的期望 E(X)存在，另一個重要的指標(biāo)是風(fēng)險載荷D(X)=H(X)-E(X),因此將PH-變換下的風(fēng)險載荷定義為：

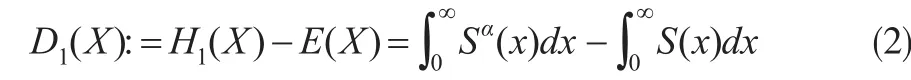
條件尾期望原理下的保費定義為：

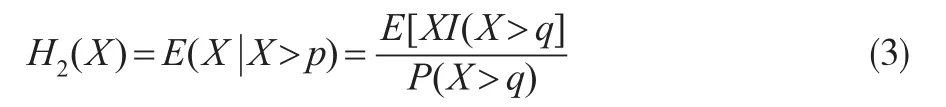
由于保險風(fēng)險常常是相互關(guān)聯(lián)的，所以本文提出一種相依結(jié)構(gòu)來分析這種相依關(guān)系。假設(shè) {ξi'i=1'2'…}是概率空間{Ω 'F'P}上的實值隨機變量序列，表示由(ξ'm≤i≤n)生成的σ-域：

i

當(dāng)n→∞時，α(n)→0，則隨機變量序列{ξi'i=1'2'…}稱為 α-混合或者強混合。強混合序列的概念最先是由Rosenblat（t1956）提出的，現(xiàn)在被廣泛用于時間序列及隨機領(lǐng)域的極限理論分析。α-混合結(jié)構(gòu)的條件要弱于其他混合，如m-相依、φ-混合、ρ-混合、絕對正則等，同時很多滑動平均混合序列和線性時間序列都是α-混合的。所以α-混合能比較合理地刻畫時間序列模型的相依結(jié)構(gòu)，有著廣泛的應(yīng)用領(lǐng)域[6]。

在概率空間{Ω 'F'P}上定義保險風(fēng)險的經(jīng)驗分布函數(shù)為：

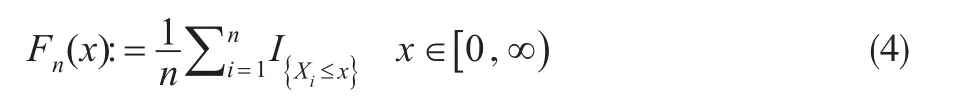
因此從式(1)至式(4)可以得到PH-變換保費H1(X)及風(fēng)險載荷D1(X)的估計量分別為：

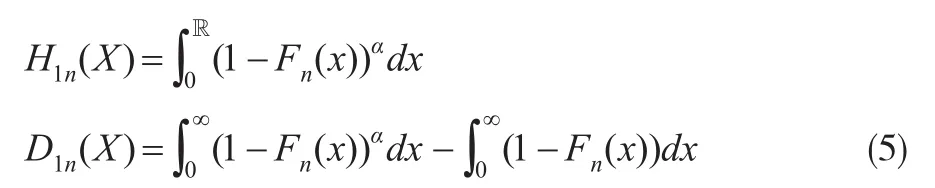
以及條件尾期望原理下的保費 H2(X)與風(fēng)險載荷D2(X)的估計量分別為：

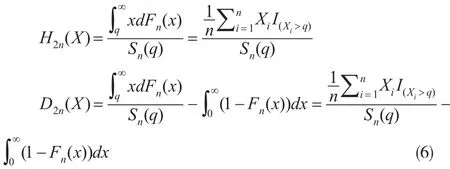
其中:Sn(q)=1-Fn(q)。

定理1：假設(shè)保險風(fēng)險{Xi'i=1'…n}是一嚴(yán)平穩(wěn)的α- 混合序列,α(n)=o(ρn)，0＜ρ＜1，如果存在 δ＞0使得EX1+δ＜∞ ，則：

定理2：假設(shè)保險風(fēng)險{Xi'i=1'…n}是一嚴(yán)平穩(wěn)的α-混合序列,如果存在1＜r≤2使得 E | X|r＜∞ 。存在θ＞(s-1)r/(r-s)使得α(n)≤Cn-θ，其中1＜s＜r，則：

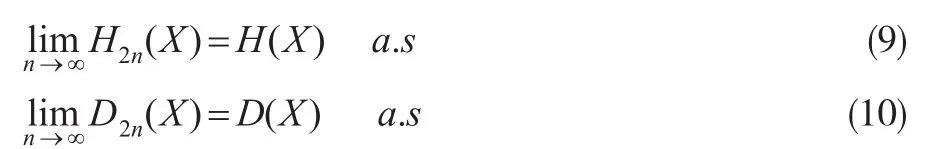
定理3：假設(shè)保險風(fēng)險{Xi'i=1'…n}是一嚴(yán)平穩(wěn)的α- 混合序列,令 ζi=XiI(X＞q)-EXI(X＞q),如果＞0,且存

i在 δ＞0 使得 E | X|2+δ＜∞,當(dāng)(k)＜∞ ，其中 δ＞0,則：

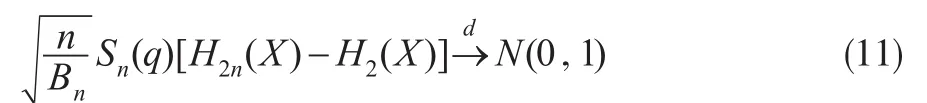
令 ψi=Xi[I(X＞q)-S(q)]-[EXI(X＞q)-S(q)EX],如果 Eψ12

i＞0,則：

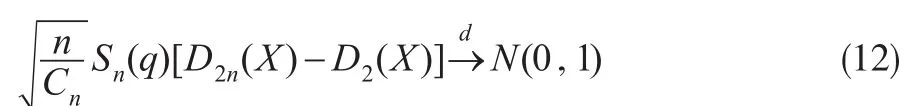
其中

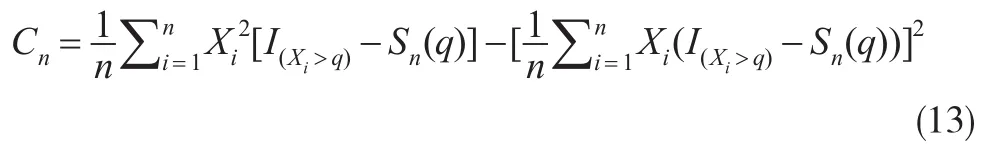
引理 1[6]：{Xi'i≥1}為 R中的平穩(wěn) α-混合序列，α(n)=o(ρn)，0＜ρ＜1，M 為大于1的正整數(shù)，則存在僅依賴于混合系數(shù)的常數(shù)C1，C2，對?0＜θ＜1，ε＞0，存在正整數(shù)r*＞0，當(dāng)正整數(shù)r＞r*時，有：

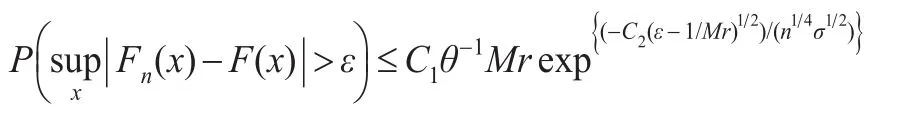
定理1的證明：

對?ω及T＞0,

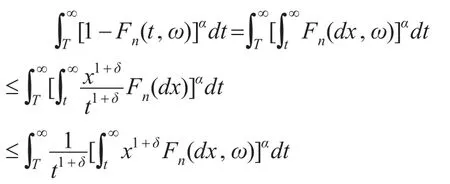
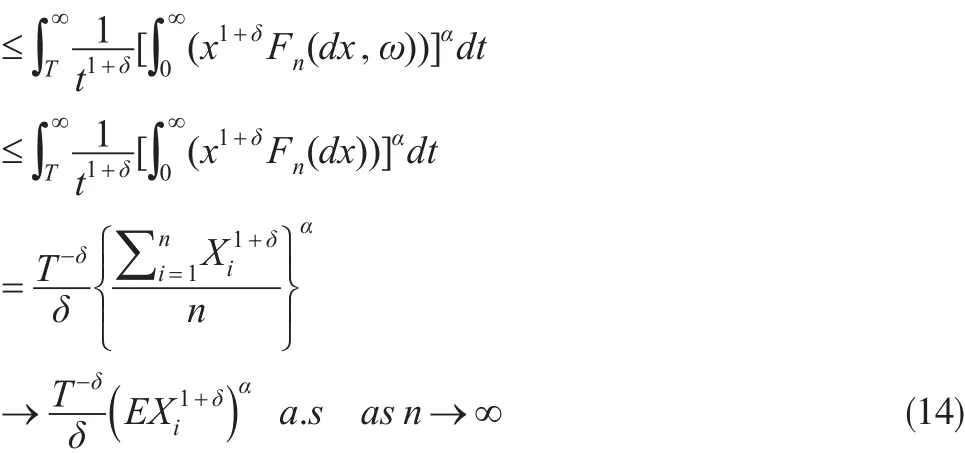
最后一個收斂結(jié)果來自于文獻(xiàn)[7]中的定理2.1。

因為 EX1+δ＜∞,所以：

由于：

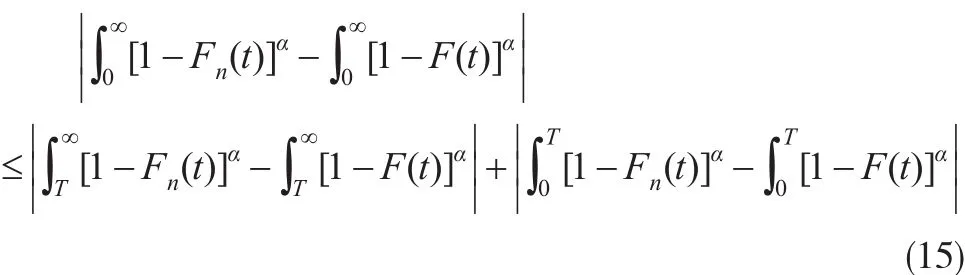
由引理1利用Borel-Cantelli定理可得：

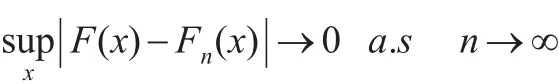
并利用α-混合序列的Bernstein矩不等式[8]，分別令n→∞，T→∞,由控制收斂定理及式(5)、式(10)、式(11),可以得到式(7)。合并上面的結(jié)果及引理1同樣可以得到式(8)。

定理2的證明：

從文獻(xiàn)[7]中的定理2.2,可以得到:由式(6)、式(16)、式(17)可得到式(9),由式(6)、式(9)、式(16)、式(17)及文獻(xiàn)[7]中的定理2.2可得到式(10)。

定理3的證明：

令

從式(13)容易得到:

由定理中假定的嚴(yán)平穩(wěn)性及 EX2+δ＜∞可以得到:

運用文獻(xiàn)[9,10]中類似方法，采用bernstein big-block與small-block程序，選擇 p=pn,q=qn,k=kn。令:

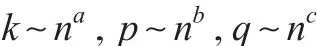
其中 a+b＜1,a+c＜1,a'b'c＞0,這些條件可以保證式(21)：

記：

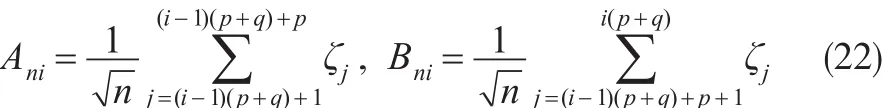
則:

由定理已知條件及式(18)至式(23)可得:

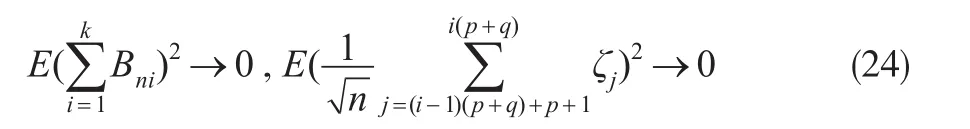
因此，由式(24)可知式(23)右端的兩項是漸進(jìn)可忽略的。

由嚴(yán)平穩(wěn)性及文獻(xiàn)[11]中的引理1。

設(shè) ρk=E(ζ0ζk)

可得:

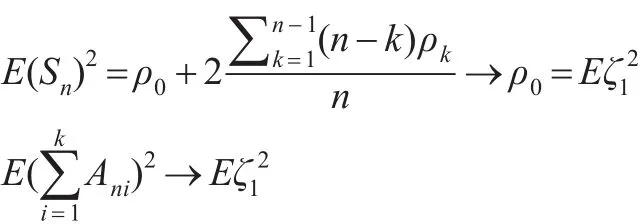
則Lindberg條件是滿足的,Lyaponov’s定理成立。

式(11)得證，同理可類似證得式(12)。

2 統(tǒng)計模擬

首先，為了保證保險風(fēng)險的非負(fù)性,從均勻分布U[0'1]中產(chǎn)生相互獨立的n+1個數(shù)據(jù)然后為了滿足本文所設(shè)定的相依結(jié)構(gòu)，令:yi=rx1+x1+i,i=1'…,n。

其中:分別設(shè)定r=0.6'r=0.3'r=0.1'n=100,200,300,α=1/2,q=0.2,名義的置信度為0.90,0.95,0.99.通過1000次重復(fù)模擬,計算相關(guān)指標(biāo)。

為了評價相關(guān)估計量的估計質(zhì)量，本文選擇了兩個指標(biāo)進(jìn)行評價，一個是估計的均方誤差，另一個是置信區(qū)間覆蓋概率。

從H1n(X)和H2n(X)這兩個估計量的MSE來看:由表1，在 r=0.1'r=0.3'r=0.6'隨著r值的增加,兩者的均方誤差總體呈現(xiàn)一種向上的變化趨勢,同時隨著樣本容量的增加,均方誤差有改善,說明相依程度與樣本容量與MSE有關(guān)聯(lián)。當(dāng)n＞200,r=0.1'r=0.3'H1n(X)的MSE略低于H2n(X),當(dāng) n＜200,看不出兩者的差別性。

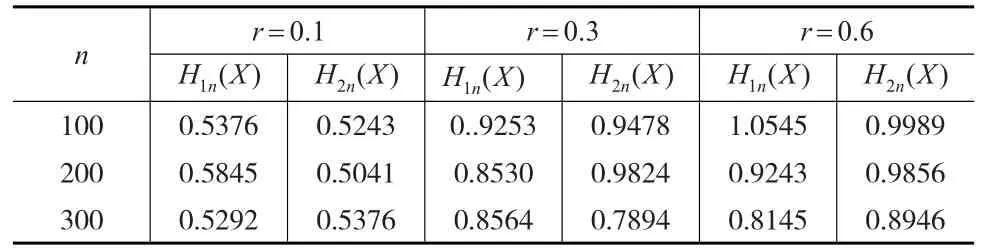
表1 MSE forH(X)

總體來說，這兩個估計量都顯示了當(dāng)r較小，樣本容量n相對較大時，估計精度優(yōu)于 r較大n較小時。

從 H2n(X)的置信區(qū)間覆蓋概率來看：由表2,在r=0.1'r=0.3'r=0.6'隨著r值的增加，計算的樣本置信區(qū)間覆蓋概率，總體上呈現(xiàn)一種與名義置信度偏離程度越大的趨勢。同時，隨著樣本的增加，偏離程度有所減小。說明相依程度與樣本容量與置信區(qū)間覆蓋概率也具有一定關(guān)聯(lián)性。總體來看，本文所提出的估計量H2n(X)估計性能是優(yōu)良的。置信區(qū)間覆蓋概率與名義置信度偏離程度的變化范圍在10%左右，特別在r=0.1，樣本容量n=300時，n=300，覆蓋概率是非常接近于名義置信度的。從不同的名義置信度來看，模擬結(jié)果并沒有顯示出優(yōu)劣性不同水平的覆蓋概率的優(yōu)劣性。

表2 Coverage probabilities forH2(X)

從上可以看出，本文所提出的相關(guān)估計量可以運用于對保險風(fēng)險相關(guān)指標(biāo)的估計，特別是在相關(guān)程度低，樣本容量較大的條件下具有更高的擬合優(yōu)度。

3 結(jié)論

在保險風(fēng)險相依結(jié)構(gòu)，即保險風(fēng)險序列是嚴(yán)平穩(wěn)的α-混合序列的條件下，本文提出了在不同保費原理下對保費與相應(yīng)風(fēng)險載荷的非參數(shù)估計方法，從理論上分析了相關(guān)估計量的強收斂性與漸進(jìn)正態(tài)性。在統(tǒng)計模擬過程中采用兩個指標(biāo)評價估計量的性能：一個是估計的均方誤差，另一個是置信區(qū)間覆蓋概率，從模擬結(jié)果來看，相關(guān)估計量表現(xiàn)出了優(yōu)良的估計性質(zhì)。可以作為保險實踐中的保費與風(fēng)險載荷的估計量。

[1]Li D Y.On Right Tail Index[D].Beijing：Peking University Press,2000.

[2]Cheng S H,Wang X Q and Yang J P.On a Kind of Integrals of Empirical Processes Concerning Insurance Risk[J].Chinese Science:Mathematics(English Edition),2003,46(2).

[3]Wang S.An Actuarial Index of the Right Tail Risk[J].North American Actuarial Journal,1997,(2).

[4]Wang S.Insurance Pricing and Increased Limits Rate Making by Proportional Hazards Transforms[J].IME,1995，(17).

[5]Wang S,Young V R,Panjer H H.Axiomatic Characterization of Insurance Prices[J].IME1997，(21).

[6]孫榮.基于隨機窗寬的α-混合序列分布函數(shù)估計[J].統(tǒng)計與決策,2016,（11）.

[7]Xing G D,Yang S C,Chen A W.A Maximal Moment Inequality for Mixing Sequences and Applications[J].Statist.Probab.Lett,2009,79(12).

[8]Chaigenxiang.Consistent Estimation of Randon Window-width Kernel of Distribution Function[J].Scientiasinica(Series A),1984,11(1).

[9]Li yongming,Yao jing,Ying rui.A Central Limit Theorem for strong Mixing Sequence and its Applicationin Regression Model[J].Mathmat-ica applicata,2016,29(1).

[10]Li Y M Li J.A Note on the Central Limit Theorem for Strong Mixing Sequences[J].Chinese J.Applied Probab.Statist.,2013,29(1).

[11]Yang S C.Bounds for Strong Mixing Sequences and Their Application[J].J.Mathematical Rasearch and Exposition,2000,20(3).