基于新維無偏灰色RBF神經網絡的居民消費價格指數預測模型

黃 洋，魯海燕，程畢蕓，許凱波

（江南大學 理學院，江蘇 無錫 214122）

0 引言

灰色理論是鄧聚龍在1982年首先提出的，是一種研究少數據、貧信息以及不確定性問題的新方法[1]。在灰色預測模型中，GM(1,1)模型是一種最常用的模型，其在工業以及數據挖掘預測等領域均已被廣泛應用。然而在利用GM(1,1)模型進行建模預測時，GM(1,1)模型有時會出現較大的偏差，存在著對數據的學習能力低，預測精度低等缺陷。RBF神經網絡是一種網絡結構簡單，所需訓練樣本少且學習速度快的神經網絡，但是隨著樣本數據的隨機性和預測樣本量的變化，RBF神經網絡的預測精度就會受到影響，從而降低了預測的精度。

為了進一步提高模型的預測精度，本文提出一種新維無偏灰色RBF神經網絡模型。

1 研究基礎

1.1 無偏GM（1,1）模型

為了消除傳統灰色模型中的指數偏差，吉培榮，黃巍松等[3]提出了無偏GM(1,1)模型。與傳統GM(1,1)模型相比，無偏GM(1,1)模型不存在傳統GM(1,1)模型所固有的偏差，因而也就消除了傳統GM(1,1)模型在原始數據序列增長率較大時失效的現象；而且在交通流預測，降水量預測，能源消耗等[4]實際問題當中有了更加廣泛的應用。此外，無偏GM(1,1)模型無需進行累減還原，簡化了建模步驟，提高了模型的計算速度。

設有原始時間數據序列，X(0)={x(0)(1)'x(0)(2)'…'x(0)(n)}，其中 x(0)(k )≥0，k=1'2'…n。

（1）對原始數據序列進行累加得到新的數據序列：

X(1)其中k=1'2'…,n。

（2）對新的數據序列建立白化方程，即：

dx(1)dt+ax(1)=u，其中a'u為系數。

（3）構建數據矩陣B和Yn：

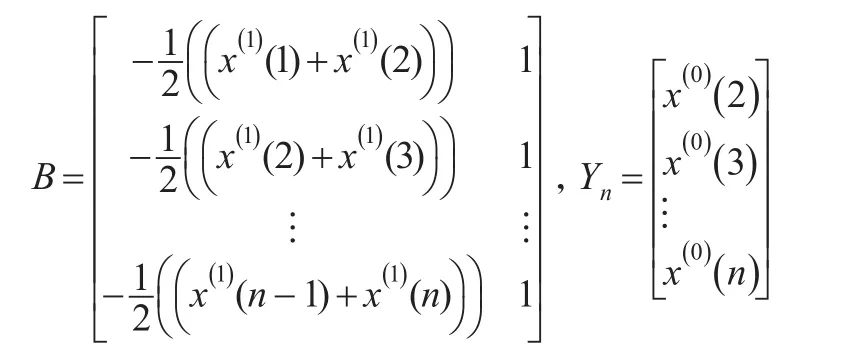
（4）利用最小二乘法求出白化方程中的系數a和u：

（5）計算無偏灰色模型的參數b和A：

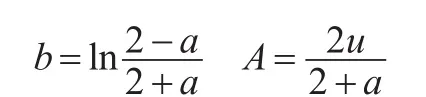
（6）建立無偏灰色模型原始數據序列模型為：

x?(0)=x(0)(1) ，x?(0)(k +1)=Aebk。其中k=1'2'…,n-1。

1.2 改進的無偏GM（1,1）模型

為了提高模型的預測精度，可以對原始數據分別進行對數函數和含參線性函數變換等[5]處理。本文通過對數變換對原始數據進行處理，具體變換過程如下[6]：

對原始數列進行對數變換：

對新的數據序列利用無偏GM（1,1）方法預測：

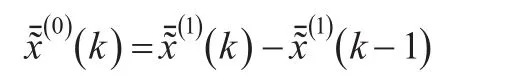
對預測數據進行指數還原：

=exˉ?(0)(k)，m?(0)即為無偏GM（1,1）方法預測值。

2 RBF神經網絡

RBF神經網絡是一種由輸入層、隱含層和輸出層組成的三層前向神經網絡。第一層為輸入層，由信號源節點組成；第二層為隱含層，從輸入層到隱含層是一種用于特征提取的非線性變換；第三層為輸出層，它對輸入模式的作用做出響應[7]。RBF神經網絡的輸出可表示為：

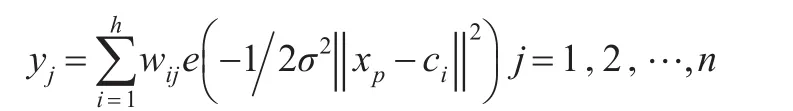
其中為第 p個輸入樣本，ci為網絡隱含層節點的中心，wij隱含層到輸出層的鏈接權值，i=1'2'…,h為隱含層節點數，yj為網絡的第 j個輸出節點的實際輸出。

3 新維無偏灰色RBF神經網絡預測模型

在灰色系統的發展過程中，隨著時間的不斷變化，一些隨機擾動或驅動因素進入系統，從而相繼影響系統的發展。而對于灰色預測模型同樣也存在這樣的問題，模型預測精度較高的僅僅是原始數據以后的1到2個數據[8]。為了提高模型的預測精度，本文提出了基于新維無偏灰色RBF神經網絡預測模型。

新維無偏灰色RBF神經網絡預測模型的建模步驟如下：

步驟1：通過對居民消費價格指數的原始數據選擇一定的維數，建立改進的無偏GM(1,1)預測模型；

步驟2：利用所求的改進的無偏GM(1,1)預測模型對居民消費價格指數進行預測，獲得對應的預測序列；

步驟3：將得到的居民消費價格指數的預測序列作為RBF神經網絡的輸入，對應的實際值作為輸出；建立RBF神經網絡模型并對其進行訓練；得到無偏灰色RBF神經網絡組合模型結構；

步驟4：在組合預測模型中，輸入需要預測的居民消費價格指數的數據序列；

步驟5：通過去掉原始序列中最開始的一個數據，加入一個無偏GM(1,1)預測值，保持數據等維，從而更新數據序列；

步驟6：返回步驟2，重復步驟2至步驟5，直到達到計算所需預測數據的精度，算法結束。

4 模型的驗證及分析

根據我國1999—2014年居民消費價格指數數據（表1，數據來源：《中國統計年鑒》2015），利用本文提出的新維無偏灰色RBF神經網絡模型進行訓練與預測。將1999—2010年的居民消費價格指數數據作為訓練樣本，建立相關的預測模型，同時將2010—2014年的數據作為測試樣本。為了驗證預測模型的有效性，本文將無偏GM(1,1)模型和無偏RBF神經網絡模型與本文提出的模型進行對比。

4.1 建立居民消費價格指數的改進無偏灰色模型

根據本文改進的無偏灰色模型的建模方法，結合表1的數據，利用MATLAB進行編程求解，求得b=0.0038，A=6.0168。將b和A的值帶入無偏灰色預測模型中可得預測結果如表2所示。該模型的平均殘差相對值為 ε?=0.863%，平均精度為：p=99.137%。

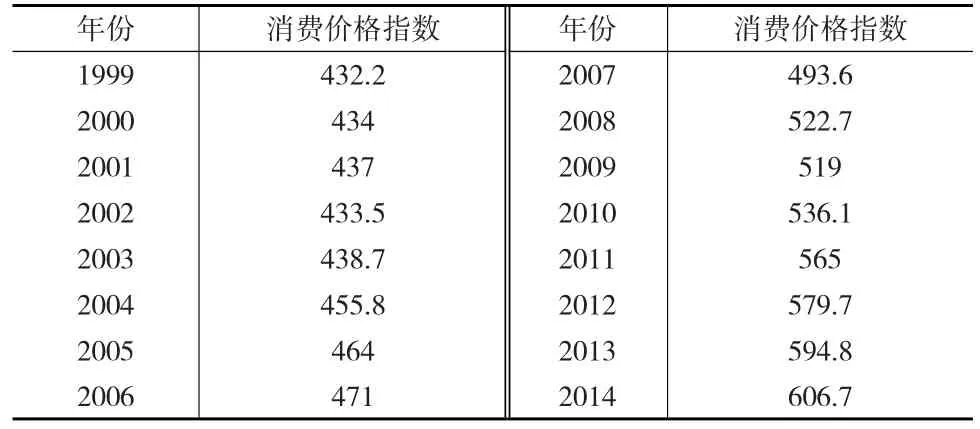
表1 1999—2014年我國居民價格消費指數

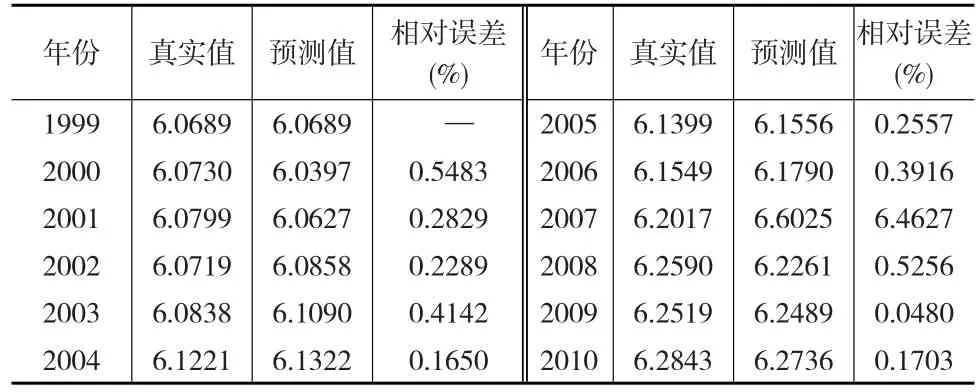
表2 無偏灰色模型對1999—2010年我國居民價格消費指數的預測值(對數值)

4.2 建立居民消費價格指數的新維無偏灰色RBF模型

4.2.1 數據處理

對原始數據取對數值后的序列進行等維處理，即去掉1999年的數據，加入利用本文改進的無偏灰色模型預測的2011年的數據值（即6.3215）。利用2000—2011年的數據建立無偏灰色模型。求得b=0.0041，A=6.0264。將b和A的值帶入無偏灰色預測模型中可得2000—2011年的預測值如表3所示。

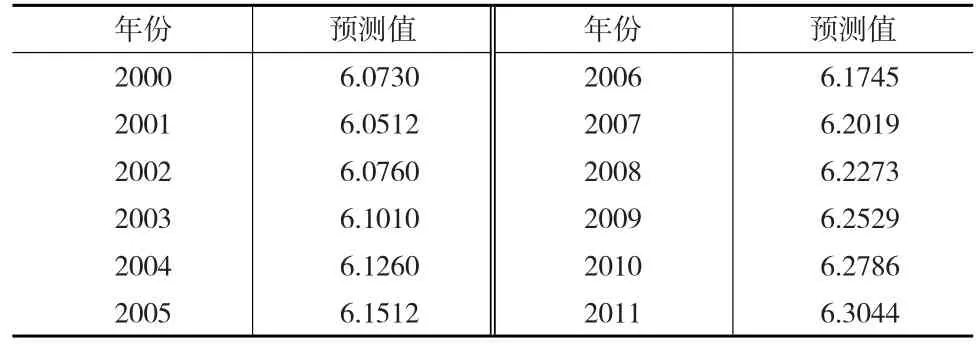
表3 2000—2011年無偏GM(1,1)預測值(對數值)

4.2.2 網絡訓練

通過利用序列的前3個時刻的值來預測下一時刻的值，即用1999—2001年數據來預測2002年的居民消費價格指數，如此循環，一直到預測2014年的居民消費價格指數。本文利用matlab建立新維無偏灰色RBF神經網絡預測模型，采用newrb進行網絡訓練，輸入層的節點數為3，輸出層的節點數為1，隱含層的節點數通過網絡訓練獲得最佳的節點數，網絡均方誤差目標值為GOAL=0.001。利用無偏灰色預測模型得到的預測值作為網絡的輸入值，對應的真實值作為網絡輸出值，去訓練RBF網絡。

4.2.3 三種預測模型的性能比較

通過利用無偏GM(1,1)、無偏灰色RBF模型以及本文提出的新維無偏灰色RBF神經網絡模型對2012—2014年我國居民消費價格指數進行預測，同時對結果進行指數變換并與實際值進行比較，所得結果如表4所示。

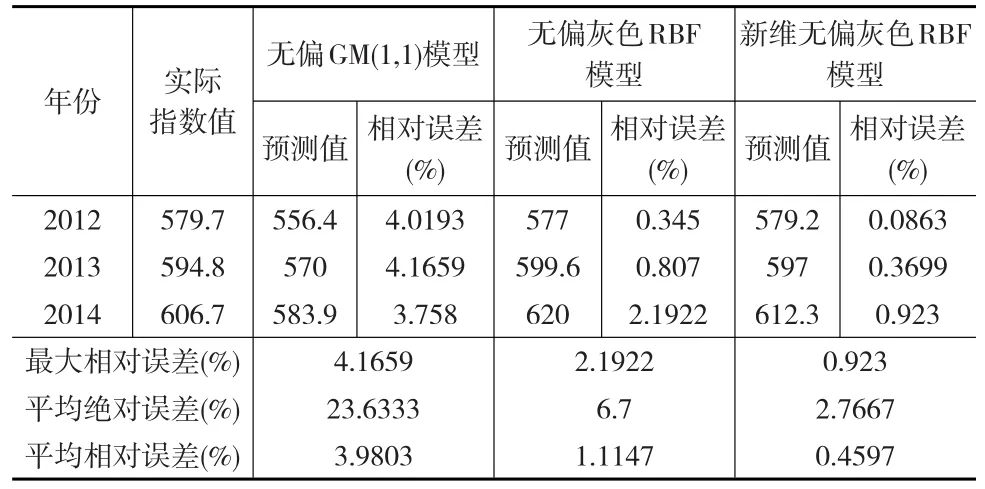
表4 各模型預測結果比較

由表4中的計算結果可以得出，新維無偏灰色RBF模型的預測結果的最大相對誤差與平均絕對誤差都比無偏GM(1,1)模型和無偏灰色RBF模型的預測結果小；并且無偏GM(1,1)模型和無偏灰色RBF模型的預測結果的平均相對誤差分別為3.9804%和1.1147%，而新維無偏灰色RBF模型的預測結果的平均相對誤差為0.46%，這說明本文提出的新維無偏灰色RBF模型的預測效果好，且預測精度高。同時利用本文改進的模型進一步預測出2015年我國居民價格消費指數值為639.2，而2015年我國居民價格消費指數真實值為615.2，相對誤差只有3.9%，因此本文提出的新維無偏灰色RBF神經網絡預測模型對我國居民消費價格指數的預測具有可行性。

4.2.4 預測模型性能的進一步比較

為了進一步驗證本文預測模型的有效性以及預測精度，本文將2012—2015年的預測值與文獻[2]中預測模型的結果進行比較，結果見表5。

表5 兩種算法性能對比

由表5數據結果可得，本文提出的模型比文獻[2]提出的預測模型的結果更接近實際值；并且文獻[2]中的模型對2012—2015年我國居民消費價格指數的預測結果的平均相對誤差為6.1546%，而本文提出的模型的平均相對誤差僅為1.3201%，說明本文模型更具有合理性和有效性，模型預測精度更高。

5 結論

（1）本文通過利用對數對原始數據進行對數變換，提高了模型的光滑度；對數據進行等維新信息處理，進一步提高模型的預測精度，再結合RBF神經網絡的極強的學習能力，從而得到了新維無偏灰色RBF神經網絡模型，使得組合模型的預測精度更高。

（2）本文利用無偏灰色模型，無偏灰色RBF模型與本文提出的模型對2012—2014年我國的居民消費指數預測結果進行比較，本文提出的新維無偏灰色RBF神經網絡模型平均相對誤差僅為0.4597%。同時與文獻[2]中的模型對2012—2015年的居民消費價格指數預測結果進行對比，本文模型的相對誤差比文獻[2]中模型的平均誤差小，只有1.3201%。由上述分析對比結果可知，本文模型的預測精度高，且與實際值較為接近。利用本文模型預測出2016年我國居民價格消費指數為646.8。這為我國以后對居民消費價格指數的預測提供一種新的方法，并從一定程度上，對我國經濟發展的預測提供一些參考數據。

[1]鄧聚龍.灰色預測與決策[M].武漢:華中理工大學出版社,1988.

[2]王麗敏.基于新陳代謝GM(1,1)模型的居民消費價格指數預測[J].價格月刊,2010,(6).

[3]吉培榮，黃巍松，胡翔勇.無偏灰色預測模型[J].系統工程與電子技術,2000,22(6).

[4]Chen S，Qu G，Wang X，et al.Traffic Flow Forecasting Based on Grey Neural Network Model[C].In Proceedings of the International Conference on Machine Learning and Cybernetic,2003.

[5]鄒慧，徐波.改進的灰色-馬爾科夫模型及其在沉降預測中的應用研究[J].工程勘察,2016,(3).

[6]陶云奇，許江，李樹春.改進的灰色馬爾柯夫模型預測采煤工作面瓦斯涌出量[J].煤炭學報,2007,32(4).

[7]聶秋平，吳敏，杜友武等.基于灰色RBF神經網絡的煉鋼煤氣消耗預測[J].系統仿真學報,2011,23(11).

[8]陳寶平.基于新維無偏灰色馬爾科夫模型的圍欄草場面積的預測[J].數學的實踐與認識,2012,43(24).