股災背景下滬深股市波動率的結構轉換特征分析
羅 君,喬高秀,王 璐
(1.西南財經大學 統計學院,成都 611130;2.西南交通大學 數學學院,成都 611756)
0 引言
2015年,我國滬深兩市單日成交額不斷刷新,各項指數不斷攀高,在6月創出歷史最高點5178;然而隨后兩個多月內,千股跌停的事件重復上演,累計跌幅高達45%。機構投資者、散戶和專家學者見證了我國股市跌宕起伏、風雨交加的形勢,從“瘋牛”到“股災”的演變過程。
研究發現,重大的政治和經濟變革、技術創新、金融風暴、新政策的出臺等因素都將引起股市收益率波動結構發生顯著變化。隨著全球金融市場波動加劇,很多學者試圖找到合適的模型來刻畫波動率的結構轉換特征。Hamilton(1994)[1]首次將馬爾科夫結構轉換機制與ARCH模型結合,建立了具有馬爾可夫結構轉換機制的ARCH模型,被廣泛地應用于金融時間序列的波動率結構變化分析。Klaassen(2002)[2]對狀態轉移GARCH模型進行改進,利用前一時刻的條件均值代替當前時刻的方差,給出了波動率多步向前預測的顯示表達。Marcucci(2005)[3]利用MRSGARCH模型分析預測美國標準普爾100指數(S&P100),發現在均方誤差作為準則的統計損失函數標準下,MRS-GARCH模型比標準GARCH模型能更精確地預測股市波動。國內學者對滬深股市波動率的結構特征也進行了不少實證研究[4,5]。
本文在已有研究的基礎上,采用Klaassen(2002)[2]的MRS-GARCH模型研究2015年滬深股市波動率結構轉換特征的異常行為。為了比較股災發生時股市波動率的異常行為,本文進一步給出了基于2005—2015年樣本的實證結果,并對MRS-GARCH模型的預測效果進行評價分析。
1 MRS-GARCH模型
1.1 模型介紹
狀態轉移模型本質是根據波動變化特征選擇不同的狀態變量,使之可確切地刻畫不同狀態的真實現狀。狀態變量st在不同狀態間轉變遵循馬爾科夫過程。其一階轉換概率為:

其中,pij表示由t-1時刻狀態i轉換到t時刻狀態 j的概率。通常說來,兩個狀態的馬爾科夫鏈狀態轉移矩陣形式為:
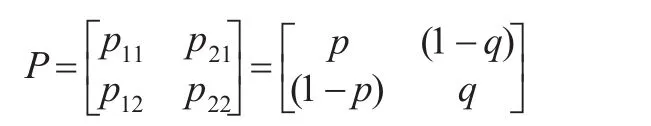
一般情況下,MRS-GARCH模型為:
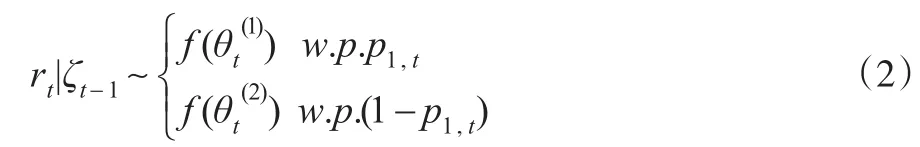
其中,f(.)表示可能的條件分布,包括正態分布(N)、學生分布(T)及廣義誤差分布(GED);θt(i)表示狀態i下不同分布特征的參數集合;p1't=Pr[st=1|ζt-1]表示t時刻處于狀態1的概率,其ζt-1涵蓋了t時刻前觀察到的所有方差信息。
確切地講,時變的參數被分解為三部分,滿足下列等式:

其中表示條件均值表示條件方差,νt(i)表示條件分布的參數。
MRS-GARCH模型包含了四個部分:條件均值、條件方差、狀態轉移機制和條件分布。從MRS-GARCH模型結構分析可知,求解rt的密度函數等價于求解條件均值、條件方差和時變條件分布的各個參數。rt的條件均值方程是一個隨機游走過程(可能存在截距項),條件方差方程是根據整個狀態路徑(包括未觀測到的路徑),其表達形式如式(4)和式(5):

其中,i=1'2,νt是一個零均值,方差為1的隨機變量。

與GARCH(1,1)模型條件方差方程類似,MRS-GARCH模型條件方差表示為:
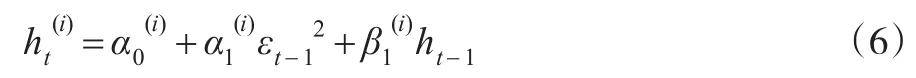
其中,ht-1代表無狀態依賴歷史條件方差。
為了規避方差依賴于過往時期的全部狀態路徑,同時便于實現多步向前預測,Klaassen(2002)[2]在Gray(1996)[6]的方法上進行改進,基于t-1時刻的條件均值代替條件方差,其表達形式為:
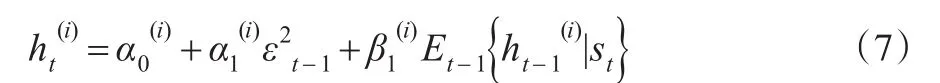
其中,t-1時刻條件均值計算為:
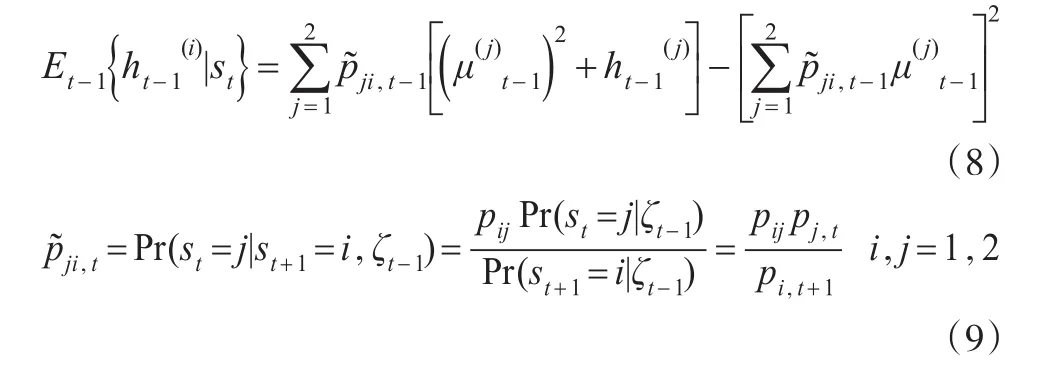
在捕捉股市收益率處于不同狀態下的特征和轉換機制時,通常使用兩種狀態(高/低波動)的MRS-GARCH(1,1)模型:
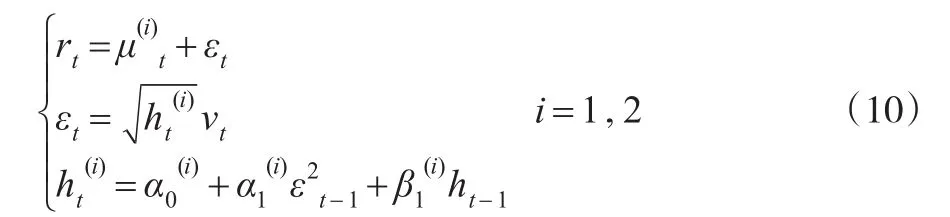
1.2 參數估計
研究表明,馬爾科夫狀態轉移模型的參數估計可以采用極大似然估計方法,但最關鍵的問題是能刻畫出先驗概率 p1't=Pr(St=1|ζt-1),即根據t-1時刻前的信息計算t時刻處于狀態1時的概率值。其一般表達式為:
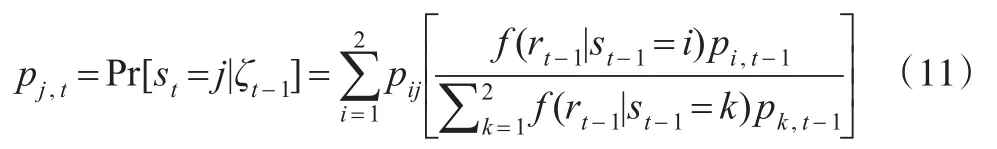
其中,pij表示t-1時刻處于狀態i到t時刻處于狀態j的轉換概率。對數似然函數如下:
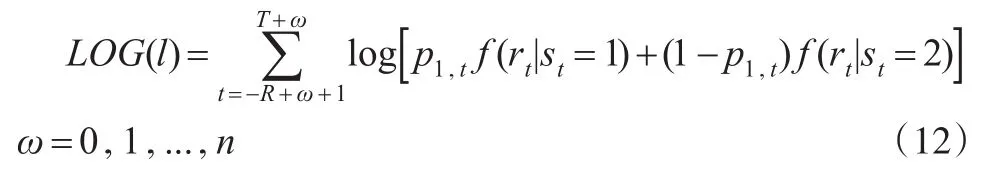
其中 f(.|st=i)表示t時刻處于狀態i時的條件分布函數。
1.3 模型預測
Klaassen(2002)[2]的MRS-GARCH模型與其他MRSGARCH模型相比有一個顯著的優點,即給出了多步向前波動預測的顯示表達,其計算公式是基于標準GARCH模型結構通過遞推的方式得到。以T時刻為預測原點,m步向前的波動預測的計算式:
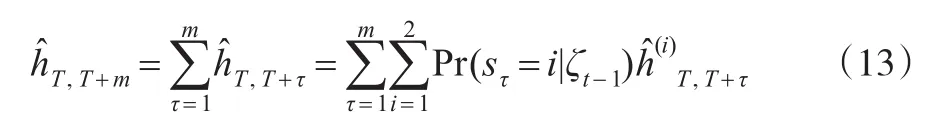
其中,表示T時刻起向前m步的方差預測之和,h?(i)
T'T+τ表示時刻T處于狀態i向前τ步的方差預測值,可以通過遞推的方式計算:
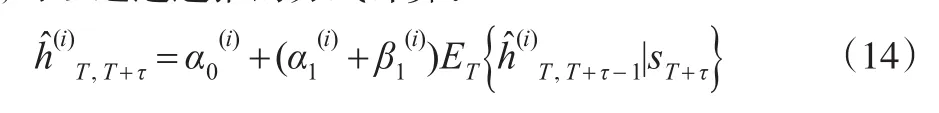
可見,多步向前的波動預測值可以通過對各個狀態下多步向前方差預測值的加權平均計算而得,其中,權重是由預測概率決定。通常情況下,計算方差預測值會采用濾波概率。其中,間隔為τ時的濾波概率為:

2 實證分析
2.1 樣本選取與描述性分析
滬深300指數作為反映A股市場整體走勢的一個重要指標,具有較好的市場知名度和較高的市場覆蓋率,能真實全面地反映市場股市的價格動態演變。因此,本文以滬深300指數日收盤價為樣本來研究滬深股市波動率的結構轉換特征,2015年全年的樣本量為237,數據來源于雅虎財經數據信息平臺。
圖1給出了滬深300指數在2015年的日收盤價和收益率。可以看出,滬深300指數收益率波動具有明顯的聚集性、突發性、時變性等特征,股市在6月達到最高點,8月跌至最低點。
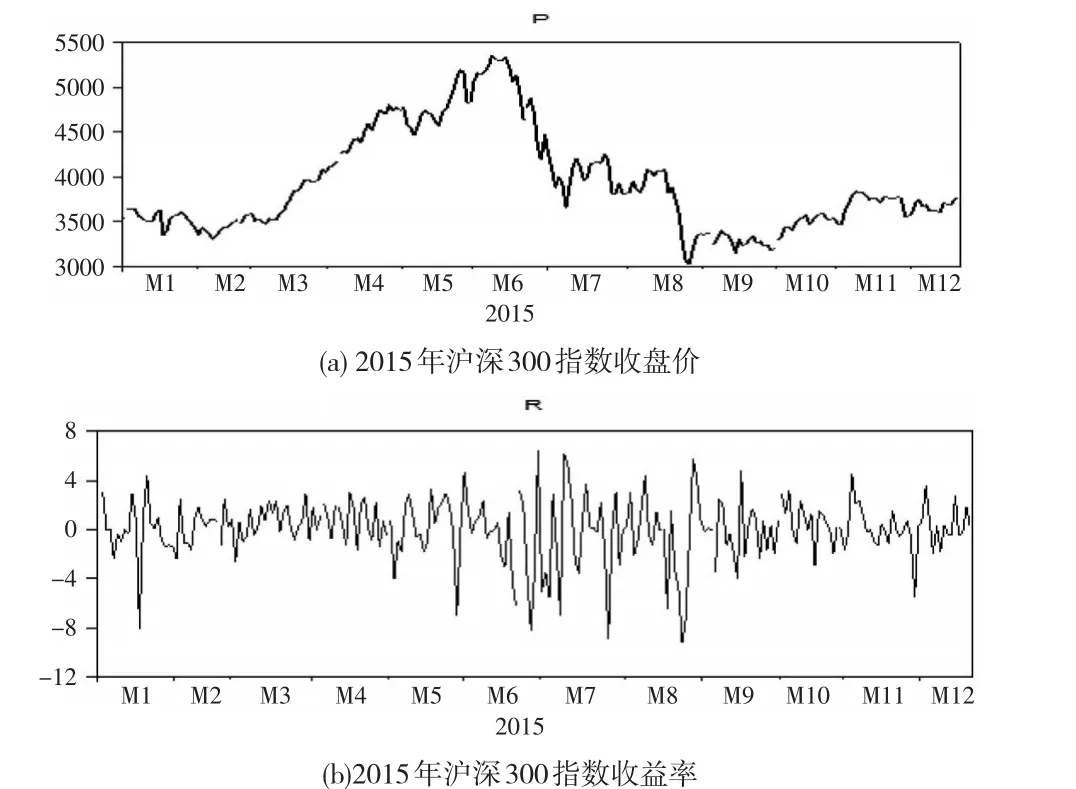
圖1 2015年滬深300指數收盤價和收益率
對滬深300指數收益率的描述性統計分析見表1。可以看到,滬深300指數收益率的峰度明顯高于標準正態分布峰度值3,且偏度小于0,則分布呈現左偏趨勢,樣本的峰度值和偏度值說明了分布呈現明顯的尖峰肥尾特征;JB統計量的值可以進一步論證收益率序列不服從正態分布;LM統計量的相伴概率 p值均小于給定的顯著性水平值0.01,表明收益率序列具有高階ARCH效應,因此本文可以利用條件異方差模型來擬合收益率的波動性。

表1 滬深300指數收益率描述性統計量
2.2 MRS-GARCH模型估計結果
本文為簡化參數估計,選取一階的狀態轉移模型,并假設模型的殘差項分別服從正態分布(N)、學生分布(T)、廣義誤差分布(GED),且認為學生分布自由度也會隨著狀態的變化而改變,用T1和T2表示低、高低狀態下的不同自由度。表2給出了通過極大似然估計方法得到的MRS-GARCH模型參數估計結果,其中,狀態1、狀態2分別表示股市處于低、高波動狀態,其中,p表示從狀態1演變到狀態1的概率,q表示從狀態2演變到狀態2的概率;ρi=α1(i)+β1(i)(i=1'2)反映高、低狀態下波動率的持續性。
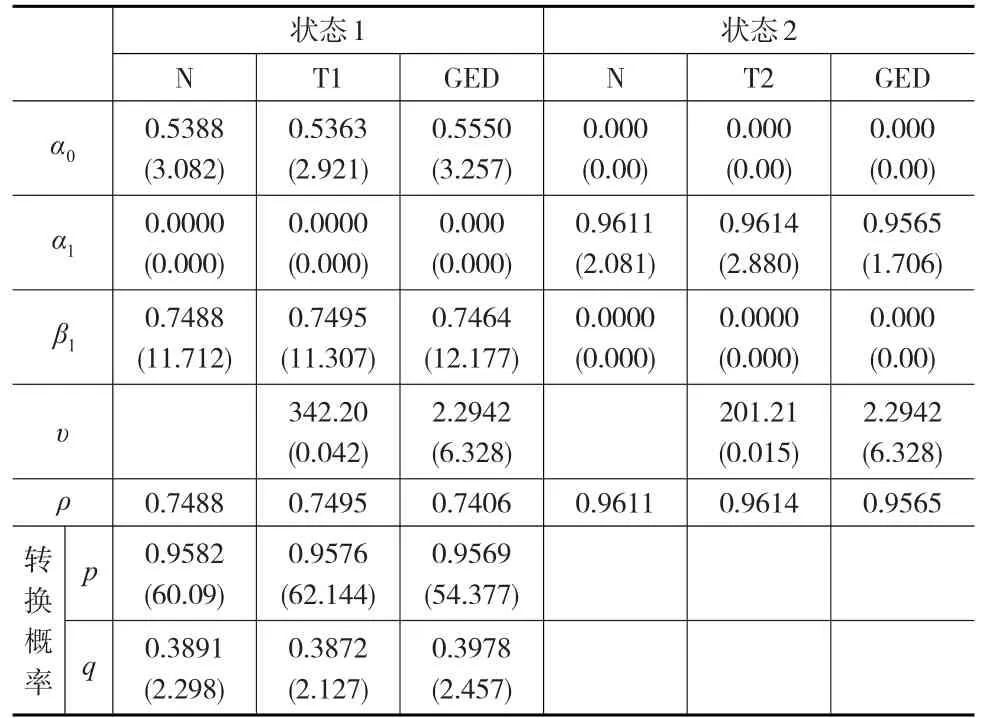
表2 MRS-GARCH模型參數估計結果(2015年)
由表2可以看出,在低、高波動狀態下,參數間存在著顯著的差異,說明滬深300指數收益率的波動存在明顯的高、低波動兩種狀態,且波動在不同狀態之間的行為也存在較大差異。在低波動狀態,影響當前期波動的主要因素是前一期波動信息,而在高波動狀態,影響當前期波動的因素主要是前一期的殘差擾動項。從波動的持續性ρi(i=1'2)結果顯示,滬深300指數波動處于低波動狀態持續性大致為0.75,處于高波動狀態持續性在0.96左右,表明2015年滬深300指數處于高波動狀態的持續性明顯強于處于低波動狀態的持續性。從轉移概率值可以發現,從低波動狀態向低波動狀態轉移概率值超過0.96,從高波動狀態向高波動狀態轉移概率值僅是0.39左右。從高、低兩狀態轉化分析,波動狀態從高向低演變的可能性(0.61)明顯大于從低向高演變(0.05),表明2015年滬深300指數收益率波動更傾向于從高狀態轉移到低狀態。
由于擾動項分布不同時MRS-GARCH模型估計先驗概率和兩狀態波動率相差不大,圖2給出了MRS-GARCH-N模型處于高波動狀態時先驗概率、以及在高、低狀態下的方差。若先驗概率值越大,滬深股市處于高波動狀態的可能性越大。圖2顯示在2015年第二季度末至第三季度,處于高波動狀態的概率值隨著時間變化高低起伏,且高波動狀態方差明顯高于低波動狀態方差,表明股市波動劇烈。這正與2015年我國股市的實際狀況吻合,股市在6月飆升至最高點,隨后開始斷崖式的跌落。
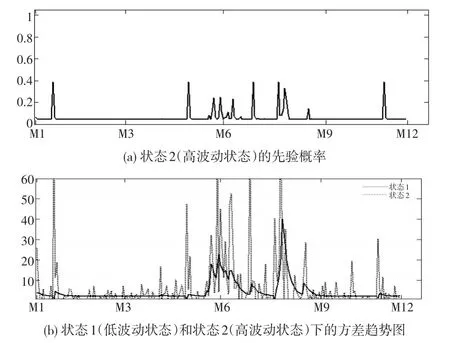
圖2 MRS-GARCH-N模型先驗概率概率和方差(2015年)
2.3 比較分析
為了與股災發生時滬深股市波動率的結構轉換特征作比較,本文進一步選取2005年4月8日至2015年12月18日滬深300指數日收盤價數據作為樣本得到參數估計結果,見表3。
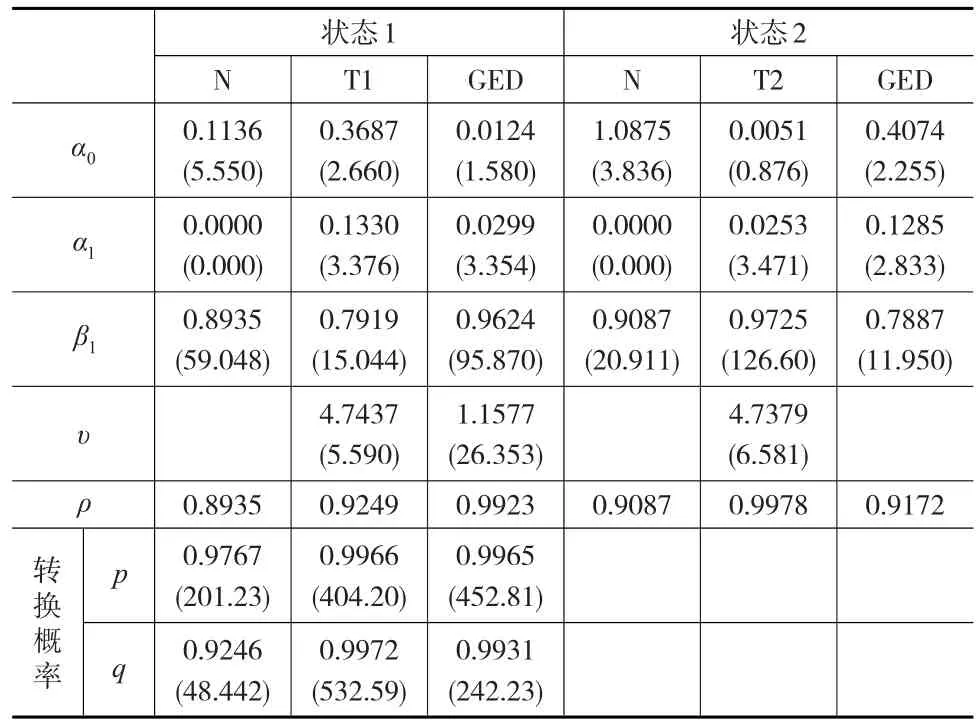
表3 MRS-GARCH模型參數估計結果(2005—2015年)
由表3可知,滬深300指數收益率的波動存在明顯的高、低波動狀態。波動的持續性ρi(i=1'2)的值均大于0.89,說明滬深300指數波動處于高、低狀態的持續性均較強;但也存在細微的差異,例如在MRS-GARCH-GED模型中,股市在低波動狀態的持續性強于高波動狀態。從轉移概率 p和q可知,滬深300指數波動更易在同類狀態間轉換,即從高波動狀態向低波動狀態演變或者從低波動狀態向高狀態波動演變的概率值均較小。
下頁圖3給出了MRS-GARCH-GED模型處于狀態2的先驗概率和兩狀態下的方差,其中黑實線表示狀態1下的方差,灰虛線表示狀態2下的方差。
從圖3可知,自從2005年開始實施股權分置政策以后,到2006年部分非流通股上市,股市波動開始逐步增強,2007年進入了高波動狀態。這可能是由于市場中股票流通量的增加以及次貸危機的影響,滬深股市在雙重因素的影響下從制高點往下跌,并一直處于高波動狀態,直至2008年美國的次貸危機演繹成全球金融危機,經濟增速緩慢,股市持續下跌,波動較低。2009年國家放松財政和貨幣政策,確立以“調結構、促銷費”經濟發展理念及市場自身調節能力,上市公司并購重組活躍,股市開始反彈上漲并處于高波動狀態;滬深股市波動經歷了2008年、2009年的大起大落,伴隨著中央宏觀經濟調控及時有效地實施,股市開始扭轉趨勢并在隨后幾年里保持平緩的趨勢,股市波動處于低狀態;2015年股市跌倒起伏,從2015年6月12日的最高點開始出現斷崖式下跌。一方面是由于中國處于經濟轉型期,監管出現漏洞,導致短期炒作、迅速套利現象顯著,另一方面是市場“融資”“融金”“配資”規模快速發展,引發股價快速持續上漲孕育了“泡沫式”的股票市場,因此導致2015年股市劇烈波動。
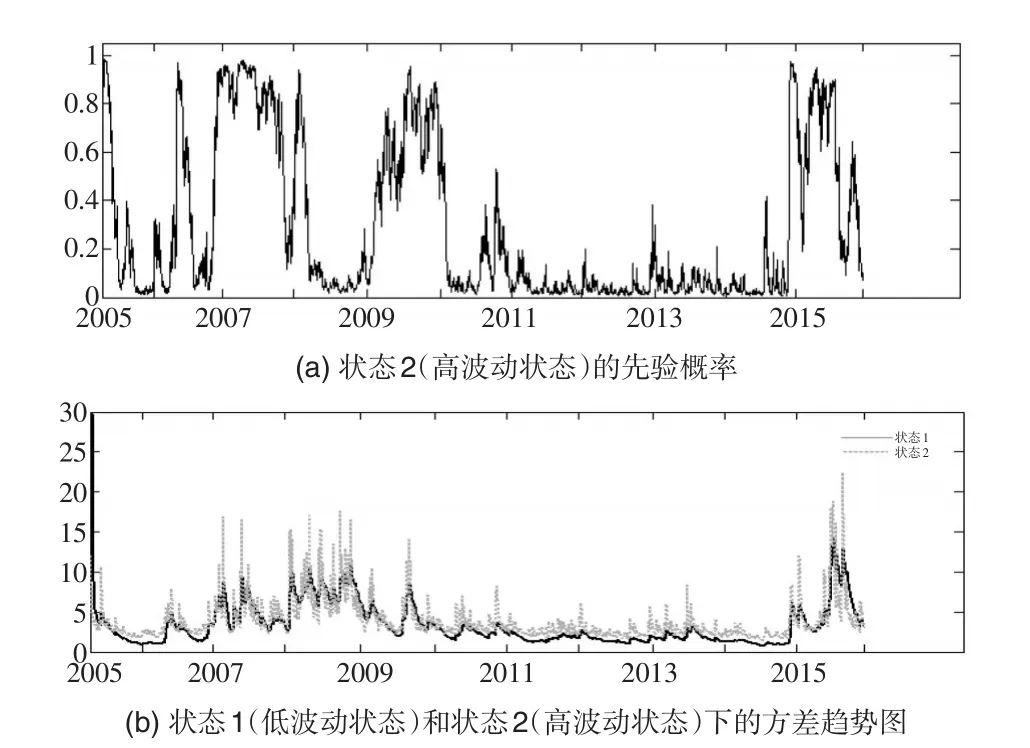
圖3 MRS-GARCH-GED模型先驗概率和方差(2005—2015)
2.4 模型評價
本文采用四個常見的統計量作為評價準則,包括AIC值、BIC值、對數似然函數(LOG(l))及均方誤差(MSE),對各個模型估計結果及樣本內的預測能力進行評價。其中:是隱含的真實波動率,是波動率的預測值。利用Marcucci制作的程序包,以對數收益率的平方近似隱含的真實波動率,通過一步窗口滾動方法,做向前一步的樣本內預測。結果見表4。
由表4可知,綜合各項評價指標表明狀態轉移模型的擬合效果和樣本內的預測能力優于標準GARCH模型,認為我國滬深股市波動存在著明顯的高、低狀態間轉換行為。2015年股災發生時MRS-GARCH-N模型擬合效果最佳,而在2005—2015年此階段發現MRS-GARCH-GED模型具有更好的擬合效果。
3 結論
本文采用Klaassen(2002)[2]的MRS-GARCH模型研究我國股市波動率的結構轉換特征,特別是2015年股市動蕩期間的表現。結果顯示,滬深股市存在顯著的波動聚集性、持續性,這與國外高度成熟的證券市場股市波動結論相似,表明我國股票市場經過十幾年的發展逐步趨向成熟。同時,滬深股市存在明顯的高、低波動,且波動在不同狀態的行為存在差異性。
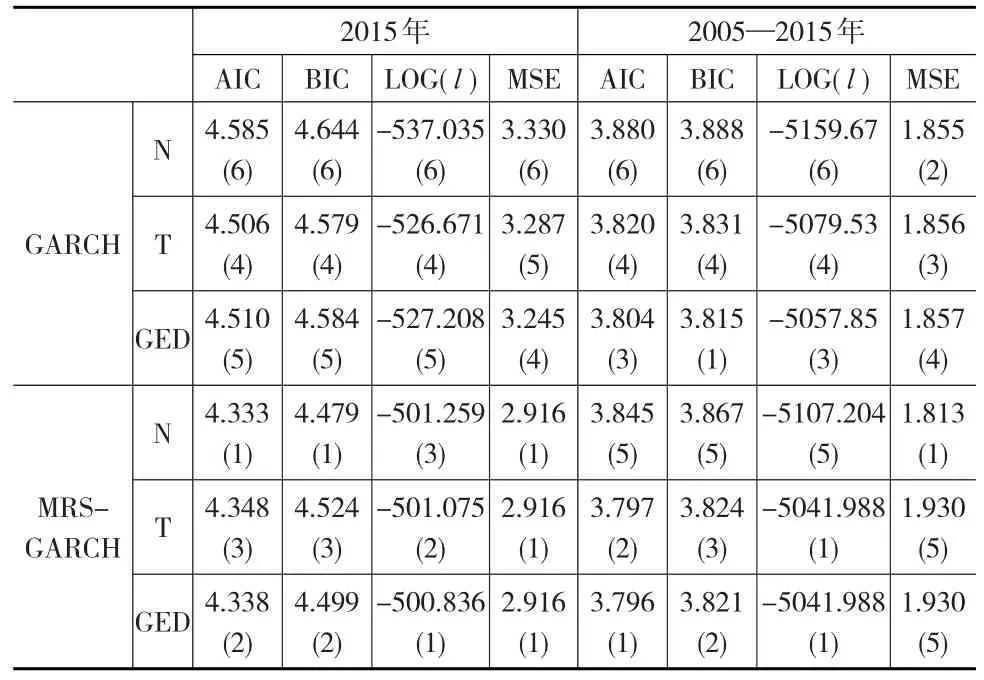
表4 各模型評價結果
滬深股市波動存在著高、低狀態間轉換行為。2005—2015年的全樣本實證結果得知滬深300指數波動更易在同類狀態間轉換,即從高波動狀態向高波動狀態演變或者從低波動狀態向低狀態波動演變的概率值均較大;然而在2015年股災背景下,滬深股市更易于從高波動狀態向低波動狀態演變(p在0.95附近,但q在0.38附近),表明了2015年滬深股市波動的異常行為。
在股災背景下,滬深股市波動處于高狀態(ρ2在0.96左右)持續性強于低狀態(ρ1在0.74左右);而全樣本擬合結果顯示股市處于低、高狀態的持續性均較強,但股市處于低波動狀態的持續性略強于高波動狀態(ρ1=0.997'ρ2=0.925)。因此,進一步說明2015年滬深股市處于高波動狀態的持續性大于整個樣本階段處于高波動狀態的持續性。
[1]Hamilton J D.Time Series Analysis[M].Princeton:Princeton University Press,1994.
[2]Klaassen F.Improving GARCH Volatility ForecastsWith Regime-Switching GARCH[J].Empirical Economics,2002,27(2).
[3]Marcucci J.Forecasting Stock Market Volatility With Regime-Switching GARCH Models[J].Studies in Nonlinear Dynamics&Econometrics,2005,9(4).
[4]劉家鵬,蘇濤.中國股市非對稱性收益的實證研究[J].統計與決策,2010,(3).
[5]趙健.不同分布下中國股市波動性解析[J].統計與決策,2014,(16).
[6]Gray S.Modeling the Conditional Distribution of Interest Rates as a Regime Switching Process[J].Journal of Financial Economics,1966,42(1).

