一般非慣性系中的剛體動力學
陳余華
(江西省大余中學 江西 贛州 341500)
黃亦斌
(江西師范大學物理與通信電子學院 江西 南昌 330022)
1 理論
在一般旋轉的非慣性系中,質點的加速度a′與其在慣性系中的加速度a的關系[1]為
a=a′+a0+α×r′+
Ω×(Ω×r′)+2Ω×v′
(1)
其中a0為旋轉系原點的加速度,Ω,α為旋轉系的角速度和角加速度,r′,v′為質點在旋轉系中的矢徑和速度.由此可以得到非慣性系中的質點動力學表達式[1]
F-ma0-mα×r′-mΩ×(Ω×r′)-
2mΩ×v′=ma′
(2)
左邊第一項為真實力,其他都是慣性力,包括牽連慣性力-ma0-mα×r′-mΩ×(Ω×r′)和科里奧利力-2mΩ×v′.這就是說,牛頓第二定律的形式在各種參考系中都是一樣的,只要加上各種慣性力.
質點系情形會如何?此時,式(2)中新增的慣性力都是外力,內力情形不變,故而各種結論不變,只要在外力項中增加慣性力項即可.文獻[2]給出了一般非慣性系中的質點系角動量定理.本文欲討論其中的剛體動力學方程.教材[3]對此有討論,但其主要使用分量語言,且主要是舉例說明.本文將使用矢量語言,并給出一般結論.


(3)
故有
(4)
這就是一般非慣性系中的質心運動定理.可見,就此而言,各處慣性力的效應只需集中于質心即可.這其實是因為,式(3)是矢徑(或速度)的一次式,而質心正是按一次式等效來定義的.

(5)


(6)


后幾項由于是矢徑(或速度)的二次式,就不可能還是那么簡單了.以下逐項分析.慣性力矩第二項等于

慣性力矩第三項等于
而科里奧利力矩為
于是,角動量定理式(5)左邊的總力矩為

將其代入式(5),即得
Ω×Ic·(ω′+Ω)
(7)

ω′×Ic·(ω′+Ω)+Ic·(ω′+Ω)×ω′+
Ic·(β′+α)

Ic·(Ω×ω′+β′+α)
(8)
式(7)和(8)就是一般轉動系中剛體對質心的角動量定理.式(4)和(8)就構成一般非慣性系中剛體動力學的完備方程組.
利用絕對導數和相對導數的關系
可以發現式(7)和(8)其實就是慣性系中的下列兩個結果[4]

可見,我們的結果正確.此外,式(5)中各項慣性力的效應,只有第一項的力矩為零,故而只有該項的合力通過質心,其他項的合力都不通過質心.
2 舉例


圖1 在旋轉的豎直平面內滾動的球

于是,質心運動定理式(4)給出

即

(9)

(10)
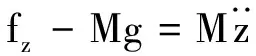
(11)
對質心的角動量定理式(8)給出
R×f=kMR2(Ω×ω′+β′)
(注意此時Ic對稱,式(8)右邊第一項為零),即
(12)
(13)
(14)
無滑滾動條件給出
即

(15)

(16)
此外還需滿足不等式N≥0和|f|≤μN.

(17)
(18)

(19)
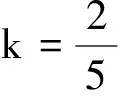

(20)
(21)
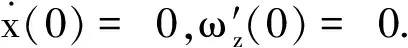
參 考 文 獻
1 周衍柏.理論力學教程(第3版).北京:高等教育出版社,2009.183~188
2 杭慶平.非慣性系中的質點組角動量定理.大學物理,1988 (1) :16~19
3 朱照宣,周起釗,殷金生.理論力學(下) .北京:北京大學出版社,1982.249~255,265
4 黃亦斌,曾建平,彭榮榮.剛體轉動方程的矢量式——兼談其與質點動力學的“內在統一性”.物理通報,2017(7):17~19

