對一道電場強度題目的3種解法與拓展分析

黃開智 仲 華 蔡靜晉

(江蘇省姜堰第二中學 江蘇 泰州 225500)

1 問題由來

近期，在對學生進行物理競賽培訓中，出現了一道關于求解電場強度的習題，題目如下：如圖1所示，一均勻帶正電半球殼，電荷量為Q，球殼半徑為R，試求球心O處的電場強度.

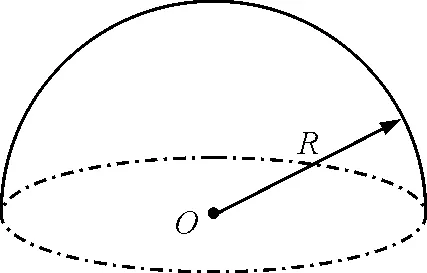
圖1 均勻帶電半球殼

2 問題分析

該題所考查的知識點主要有兩個，一是點電荷的電場強度計算公式，二是電場強度的矢量性.高中生解該題，要求學生有較強的數學基礎，主要是微積分，另外也需要良好的空間想象能力和知識類比遷移能力.針對此題，主要有如下思考觀點.

觀點1：該題的解答必須要使用微積分，并且積分路徑取決于微分思想，大致有3種思路.一是旋轉積分，如圖2所示，先求出半環在圓心處的場強，然后將半環水平旋轉360度積分，便得到球殼在球心處的場強；二是疊加積分，如圖3所示，先求出一個微分環帶在球心處的場強，然后將環帶在豎直方向疊加積分，求出球心處的場強；三是面積分，如圖4所示，先求出面積元dS在球心處的場強，然后對面積進行積分，得到球心處的場強.

圖2 旋轉積分

圖3 疊加積分

圖4 面積分

觀點2：該題的解答如果要使用積分，便超出了學生常規的能力范疇，故而必定有其他等效的方法，可以較為便捷地得到答案.

3 問題解決

針對積分思路，本文給出兩種解答過程，如下.

解法1：旋轉積分

如圖2所示，假設實心半圓環攜帶均勻正電荷，電荷量為q，在環上選取線元dl，故其電荷量為

考慮到該場強的水平分量相抵消，只有豎直方向的分場強，用dEy表示，則

對dEy進行積分，便得到半圓環在圓心O處的場強大小

最后將半圓環進行水平轉動360°，便得到球殼，且球殼電荷量等于無數個半圓環的電荷量的和，即Q=∑q.故而在球心處，半球殼的場強大小為

方向豎直向下.

解法2：面積分

如圖4所示，在球殼上選取面積元dS，其電荷量為

利用球坐標面積元微分公式

dS=R2sinθdθdφ

則

該面積元電荷在球心O處場強的豎直分量為

于是利用雙重積分

整理得到球心處的場強大小為

方向豎直向下.

解法3：等效思維——馬德堡半球實驗

如圖5所示，假設在球心處固定一電荷量為q的帶負電小球，然后在球殼處選取面積元dS，其電荷量為

q對dQ的電場力為

于是該力對應的壓強應為

由于在球殼上的壓強處處相等，故可以將這些壓強等效為大氣壓強，其物理情境便類似于“馬德堡半球實驗”.大氣壓強p0產生的壓力作用在球面上，球面的等效面積為半球截面πR2，則壓力大小為

F=p0S=πR2p0

將大氣壓強p0換成電場力產生的壓強p，故作用在球殼Q的電場力

消去q，得出球心處場強大小為

方向如圖5所示，豎直向下.

圖5 等效思維——馬德堡半球實驗

4 問題感悟

上述解法2和解法3的結果一致但與解法1的結果不同，有如下幾點思考.

第一,解法1的結果是錯誤的.其錯誤原因在于微分思路有問題，當半圓環水平旋轉dφ時，形成的是如圖6所示的“弧帶”，而在該“弧帶”上，隨著θ角的增大(向下轉動)，dθ角對應的電荷量也在增大，它不能等同于寬度一致的圓環的電荷分布.如同沿著“經線切西瓜”，總有下面西瓜片要比上面寬.因此，該解法的微分思路有問題，要做修改，而修改后，就變成了解法2的面積分了.

圖6 弧帶微分

第二,解法2遵循了嚴格意義上的積分思想，應該不存在什么問題，但其難點在于球坐標的微分面積元公式的記憶和基本積分運算，屬于高等數學知識內容，超出了學生的能力范圍，學生只有通過一定的數學培訓后，才可能求解結果.

第三,解法3先是在球心處引入點電荷q，球殼對點電荷的電場力大小等于點電荷對球殼的作用力，再將該作用力所產生的壓強等效為大氣壓強，利用馬德堡半球實驗規律，求出電場力的大小，進而得出場強.該解法思路巧妙，主要運用了等效思維，是在高中生能力范圍之內的解法.此外，從高中物理學科核心素養來看，發展學生物理核心素養主要從“物理觀念”“科學思維”“科學探究”和“科學態度與責任”4個方面做起.解法3的等效思維實際上突出了科學思維中的模型構建，從物理學的視角，找出模型之間的內在規律及相互關系，進行分析綜合，這有助于提升學生提出創造性見解的能力與品質，故而本文推薦該種解法.

5 問題拓展

若將該題改為如圖7所示，不求球心O處的場強，而是求距球心O正下方h位置處的A點的場強.此時，再利用等效思維，便無從下手，只能借助面積分，而積分的難點在于計算，分析過程如下.

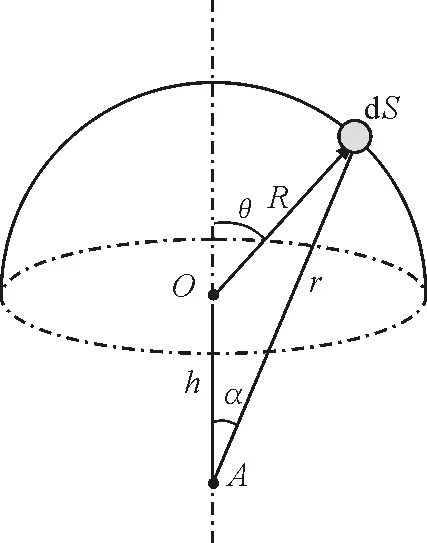
圖7 均勻帶電半球殼

第一步，建立球坐標，選取面積元,如圖7所示.則

該面積元在A點產生的場強為

第二步，算豎直分場強

dEy=dEcosα

其中

第三步，對φ和θ積分，求解場強E.

積分過程極其復雜，要換一種思路.求解電場強度的另一種方法是可以先求解電勢φ[1]，利用電場強度與電勢關系E=-φ，再求解場強，其優點在于電勢的求解是標量疊加，容易理解，可降低積分難度.

6 總結

高中階段，對學有余力的學生，在競賽培訓的過程中，應該重視物理思維的培養，提升學生的問題分析能力和物理建模能力，如上文“解法3”所運用的等效思維.不可否認的是，數學運算能力，特別是高等數學部分內容較為重要，但不能過分依賴數學運算，而忽視了物理本質.

參 考 文 獻

1 黃開智.帶電體的電勢及場強求解方法.物理之友，2015，31(11)：36～38