FSC橫向穩定桿設計及有限元分析

陳柯序 周怡潔 楊靂

1.西華大學西華學院 四川省成都市 610039 2. 西華大學汽車與交通學院 四川省成都市 610039

1 引言

大學生方程式賽車（FSC）中常采用雙橫臂獨立式懸架，特點是車質量輕，比功率大，在快速轉向時兩側懸架發生不等量變形大，引起車身側傾，會極大程度上影響賽車的彎中姿態和轉向特性，此時需要橫向穩定桿提供抑制車身側傾的力矩，增加懸架的側傾角剛度，以提升賽車的操穩性。

橫向穩定桿（anti-roll bar），其固定在左右懸架的下臂。（其基本結構如圖1）賽車在轉彎時作用在車的滾動中心的離心力造成車身的側傾，側傾后，簧上質量加劇側傾，導致賽車彎內輪和彎外輪的減震彈簧拉伸和壓縮，載荷轉移，造成橫向穩定桿的桿身扭轉，其利用桿身被扭轉產生的反彈力來抑制車身側傾。

設計橫向穩定桿時，除了要考慮整車總的側傾角剛度外，還應考慮前后懸架的側傾角剛度之比。賽車設計中根據車手的駕駛習慣不同，常常會將前后懸都裝上穩定桿，調節到略微轉向過度（就個人駕駛習慣而言）。最理想的狀態是把橫向穩定桿所提供的側傾角剛度控制在懸架的總側傾角剛度的20%~50%之間。

圖1 橫向穩定桿位置布置

2 橫向穩定桿側傾剛度計算

汽車上懸架系統的穩定裝置可以裝與縱向，也可裝與橫向，對于二軸汽車，在前軸或是后軸加裝需要經過具體的分析來匹配整車的性能[1]。在進行穩定裝置的匹配過程之中，縱向的相對來說便于計算，而橫向的穩定桿卻相對較復雜一些。它必須由整車操穩性和車身的受力狀況兩大因素綜合考慮決定。主要是通過對橫向穩定桿的設計來控制前后軸角剛度K1和K2的分配關系[2]。換言之，控制前后角剛度的比值λ=K1/K2。

首先需要考慮的是一個合理的轉向特性。車軸的偏離角的大小是與該車軸的角剛度成正比的。通過橫向穩定桿來調整整車的角剛度在前后軸上的分配，可以改變前后軸的偏離角的大小。進而改變整車的轉向特性趨勢。但是，這僅僅是考慮了橫向穩定桿的單一作用下的結果。實際中整車的轉向特性是由多方面因素共同決定的，如軸荷分配、結構參數、輪胎材料等。所以，單單是橫向穩定桿還不足以完全決定整車的轉向特性，于是，為了解決這一問題，將橫向穩定桿的剛度設計為可調式的結構，以便可以提供更多的選擇，來滿足不同車手的駕駛習慣，這對于后期的賽車調教頗為重要。

其次，當汽車過彎時，在側向加速度的作用下，由于各軸質量的大小和重心高度不一致，懸架的布置也會有一定的差異，于是便導致了各軸所承受的力矩也就不一樣。如果此時不能使在前后軸的側傾力矩保持一致，那么，車身就會受到一個額外的附加力矩，這往往是我們不希望看到的。所以，為了保持車身在各軸處的側傾角相等，那么整車的側傾角剛度在各軸上的分配則必須保持相互對應的關系。

所以，橫向穩定桿在整車上的安裝是需要綜合考慮的問題。當然，首先我們要解決的就是橫向穩定桿剛度的計算問題。橫向穩定桿的設計在達到所需性能的同時必須滿足其強度要求。同時汽車設計愈來愈追求輕量化，這一源于賽車運動的概念具有著巨大的優勢。越輕的重量，可以帶來更好的操控性，加速性，同時亦會有出色的節油表現。所以穩定桿的設計也應該滿足這一概念，保持輕量化理念。

橫向穩定桿實質上就是一根軸向扭動的彈簧機構[3]，簡化的結構形式如圖2、圖3所示。中部的兩端一般通過橡膠襯套支撐在車架/車身上。

設橫向穩定桿BC長度為l，AB長度為l1，AB與BC的夾角為θ。現在A點作用一垂直于紙面向里的大小為F的力，則在D處作用有一大小相等，方向相反的力F1。此時BC中點截面的扭轉角為0。側傾角剛度的計算公式為：

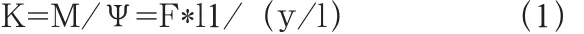
此次計算過程中忽略了橫向穩定桿的彎曲過渡圓角以及橡膠襯套的彈性變形，對橫向穩定桿側傾角剛度的影響。同時，由于車身的側傾角由于較小，故假定A、D兩點為小變形狀態[4]。

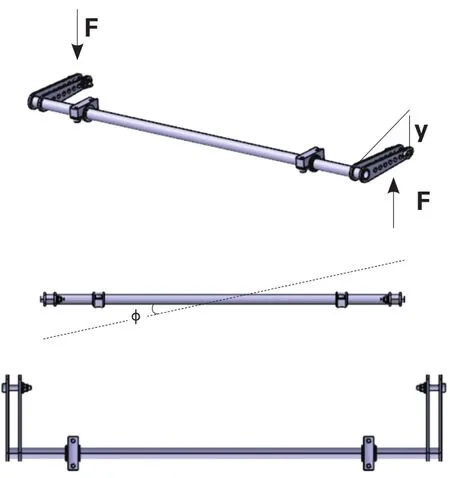
圖2 橫向穩定桿受力簡圖

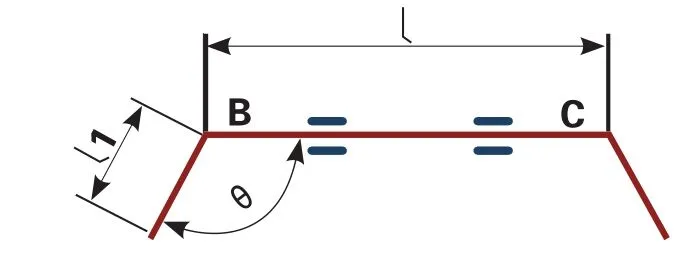
圖3 橫向穩定桿模型簡化圖

則此時橫向穩定桿的側傾角剛度的側傾角剛度計算公式[5]為：

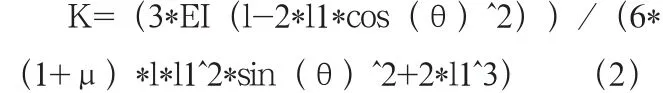
其中：E為彈性模量；I為截面慣性矩；μ為泊松比。

觀察公式不難發現，影響到橫向穩定桿的側傾角剛度的主要因素為：所選材料的彈性模量、泊松比、桿身長度、擺臂長度、截面極慣性矩（若為圓管，則為圓管的內外徑）、桿身與擺臂的夾角等。

當橫向穩定桿制造完成后，我們很難做到改變橫向穩定桿的材料、桿身的長度以及夾角等影響因素。所以，為了實現橫向穩定桿剛度的可調，常見的做法是通過改變擺臂l1的長度進而快速調整剛度的大小。

通過VB編程將公式做成程序（見附錄），達到快速求解的目的。如圖4所示。

進行設計時對橫向穩定桿的壽命要求并沒有民用車那么高，所以本次設計舍棄了國內常用的60Si2MnA材料，采用了4130空心鋼管作為橫向穩定桿的主體部分。橡膠襯套以其良好的隔振性能，具有所期望的彈性特性及衰減特性等優點，成為汽車懸架中不可缺少的重要元件。然而在橫向穩定桿中，橡膠襯套會損失一部分能量，進而影響到橫向穩定桿的側傾角剛度，故選用了尼龍襯套代替橡膠襯套，減少這種能量損失，使上述的計算公式更加趨近于真實的值。兩端擺臂則以45鋼材料制成作為其傳力元件。同時為使焊接方便，將θ的角度值定為90°。

圖4 橫向穩定桿側傾剛度計算程序

設計的橫向穩定桿需提供的側傾角剛度為300.00Nmm/°，選取了橫向穩定桿的主體鋼管的長度l為500mm，通過V B程序快速計算出所需的關鍵尺寸：穩定桿長度l=500mm；擺臂長度l1=69.8mm；鋼管外徑D=16mm；鋼管內徑d=12mm；夾角θ=9 0°，計算出側傾角剛度K=299.84Nmm/°

3 橫向穩定桿有限元分析

3.1 三維模型的建立

ANSYS具有完善的數據接口，能與絕大部分計算機輔助軟件實現數據的共享和交換，如SOLIDWORKS，CATIA等。根據上述選取的零件尺寸，對橫向穩定桿在CATIA之中進行三維實體建模。然后在導入ANSYS之中轉化為有限元模型，完成有限元分析的前處理中的第一步。三維模型渲染如圖5所示。

由于橫向穩定桿兩側完全對稱，為相對獨立的元件，故在ANSYS Geometry中將此結構簡化為一半，同時也可以減小網格劃分的數量，縮短求解時間，如圖6所示。

圖5 橫向穩定桿三維模型渲染圖

圖6 橫向穩定桿ANSYS分析簡化模型

3.2 材料參數

ANSYS的材料庫可以快速的添加自己所需的材料，經過查表，獲取到所需的具體材料參數如下：

彈性模量（pa）泊松比密度（kg/m3）屈服強度（pa）4130鋼管 2.11E+11 0.279 7850 7.85E+08 45鋼 2.09E+11 0.269 7890 3.55E+08尼龍 8.30E+09 0.280 1400 6.89E+07

3.3 網格劃分

網格劃分的主要目的是對橫向穩定桿模型實現離散化，將需要求解得出精確結論的地方劃分為適當數量的單元。當劃分的單元數量較多時，會需要更多的計算時間，過少會導致結果失真，所以需要適度把控網格數量與計算精度之間的關系。我們可以選擇在需要關注的結構處劃分更加細致的網格，而不必要的地方則進行略微粗糙的網格劃分。

汽車橫向穩定桿的結構比較簡單，采用實體單元自動劃分網格[6]。將橫向穩定桿的擺臂部分的網格大小劃分為0.5mm，桿身部分的鋼管為1mm，而其余部分則將網格大小控制為2mm。劃分方法全部為Automatic。

最終網格劃分的結果為Nodes數為375404，Elements數81307，在Element Quality中查看網格的劃分質量：最小值為0.1555，最大值為0.99999，平均值為0.93249.結果如圖7。網格的質量完全符合所需要的分析要求。

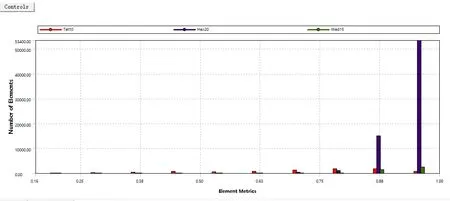
圖7 ANSYS網格劃分質量圖

3.4 靜力學分析

經過分析，對橫向穩定桿施加載荷。經推桿傳遞至擺臂的力為830N左右，實際施加時將力放大為900N，作用于擺臂上最遠處的孔內。橫向穩定桿在桿身中間截面的扭轉角為0°，故在此截面施加一固定約束。橫向穩定桿安裝座部分焊接在車架處同樣施加一固定約束。然后對橫向穩定桿做靜力學分析，得到穩定桿的應力云圖。結果如圖8所示。

由圖所示，最大應力出現在橫向穩定桿桿身和擺臂的連接處，最大應力為489.42Mpa，4130鋼管的屈服強度為785Mpa，遠遠小于此屈服強度值。擺臂上最大應力大約在220Mpa，45鋼的屈服強度為355Mpa，同樣是小于此值，所以該橫向穩定桿的設計能夠滿足其強度要求。

圖8 橫向穩定桿應力云圖

4 結語

對于具體的汽車來說，是否需要增加橫向穩定裝置，主要還是要看整車的角剛度是否夠大。當選取了較小的彈簧剛度時，則可以添加橫向穩定桿以彌補整車的總角剛度。

在計算橫向穩定桿的側傾角剛度時，忽略了襯套的彈性變形對橫向穩定桿的側傾角剛度的影響，在追求一個比較準確的值時，此部分能量損失是應當被計算的。本次設計選取了橫向穩定桿的一種最簡單布置形式，使計算過程趨向簡單。

橫向穩定桿在懸架中的安裝應盡量安裝在車軸的正上方，以避免使車軸受到額外的附加載荷。同時，由于懸架部件是相對于車身為運動狀態，應當對橫向穩定桿進行運動干涉的檢查，在設計之后，需要進行橫向穩定桿軌跡的校核。