多維立體探究 讓素養落地生根
——《多邊形的內角和》教學與評析

執教/錢兆蘭 評析/劉德宏

【教學內容】

蘇教版四年級下冊第96～97頁。

【教學過程】

一、聯系舊知，引入新課

師：同學們，圖形是我們數學學習的重要內容，你知道哪些圖形？

生：三角形、正方形、長方形……

師：大家說到的一些圖形，我們用三角板就可以拼出來（課件逐個出示三角板拼成的部分實圖：三角形、長方形、正方形、平行四邊形、四邊形、五邊形……），給我們的三角板越多，拼成的圖形形狀也就越多（課件出示三角板實物隱退后的抽象圖形）

師：像這些由三條或三條以上的線段首尾相接圍成的平面圖形，它們有一個共同的名字，叫多邊形。（板書：多邊形）

師：三角形是最簡單的多邊形。

師：在多邊形中我們已經知道三角形的內角和是180°，你想到什么新問題呢？

生：四邊形、五邊形、六邊形等其他多邊形的內角和又分別是多少度呢？

師：問題提得真好!是呀，四邊形、五邊形、六邊形等其他多邊形它們的內角和又分別是多少度呢？這當中有沒有什么規律呢？今天這節課我們一起來研究多邊形的內角和。

【評析：學生已經知道三角形的內角和是180°，這是本課教學的知識生長點，“三角板拼圖形”不僅讓學生感悟圖形之間的關系，更順勢引導學生聯系舊知自主推理產生疑問，讓學生從發現問題、提出問題開始真正經歷規律的探究過程，并為接下來的“四邊形內角和探究”埋下伏筆。】

二、新課探究

師：我們已經知道三角形的內角和是180°，下面讓我們從四邊形開始，展開對多邊形內角和的研究。課件上正好有幾個四邊形，你覺得它們的內角和是多少呢？

生：360°。

生：我也覺得是360°。

師：為什么？你是怎樣想的？

生：正方形、長方形是四邊形，四個角都是直角，4個90°是360°，那么，我想其他四邊形的內角和也是 360°。

生：我的想法和他一樣。

師：我們可以確定正方形、長方形的內角和是360°（課件在正方形、長方形四個內角處添加直角符號），但其他四邊形的內角和到底是不是360°呢？讓我們小組合作開始探究。

1.探究活動：小組合作探究四邊形的內角和是多少，初步感受分割法。

師：請大家以小組為單位，選擇方法來探究“四邊形的內角和是不是360°”。

課件出示活動要求：①任選一個四邊形作為研究對象，標出其所有內角；②小組商議，確定驗證方法后動手實踐；③操作完成后，推選代表準備發言交流。

（學生分組探究活動）

師：下面請每個小組將本組的驗證方法與結論和大家交流。

生：我們組用量角器分別量出4個角的度數后相加，發現四邊形的內角和是360°。

生：我們參考以前學習三角形內角和的方法，把四個角撕下來拼到一起，發現剛好拼成一個周角，我們認為四邊形內角和是360°。

生：我們沒有量也沒有撕，我們小組從剛才用三角板拼圖形得到啟發，加了一條線把四邊形分成兩個三角形，再用 180°×2就得出這個四邊形的內角和是 360°了。

師：沒有量也沒有撕，只加一條線，聽起來很簡單，給大家具體說說。

生：（實物投影）從頂點到相對頂點連一條線將四邊形分割成兩個三角形，原來的四個內角被分割成了六個角，分別在兩個三角形中，三角形的內角和是180°，再用180°×2就求出了四邊形的內角和是360°了。

師：“求四邊形的內角和”可以轉化成“求兩個三角形的內角和”（課件將學生展示的再逐步呈現），兩個三角形一共六個內角的和就是四邊形的內角和，分割、轉換是我們學習數學知識時經常用到的重要的數學方法。

師：有結果不是360°的嗎?

生：沒有。（若有，關注方法及測量誤差）

師：那還有不同證明方法嗎？

生：沒有了。

師：好，我們現在可以確認“任意四邊形的內角和都是 360°”。

師：量、撕、分割三種方法，你更喜歡哪種方法？

方法優化：運用“分割法”將多邊形分成幾個三角形，幾個三角形的內角和就是多邊形內角和的方法較簡單。

【評析：四邊形的內角和是探究多邊形內角和的第一層面紗，從“自然量”、“ 按需撕”到“嘗試分”求和是重要的思維跨越，給足時間、空間，引導學生數形結合，自主思考，小組合作探究初步感知規律，滲透數學思想，發展思維。】

2.探究活動：引導多維思考，自主探究五邊形、六邊形的內角和，優化分割方法。

師：下面請大家從材料袋中取出老師給大家準備的五邊形，求出它的內角和。

（學生自主操作，教師巡視）

（匯報交流）

生：我分割成了3個三角形（教師引導學生感受從任意一個頂點出發分割），180°×3=540°。

生：老師，我和他不同，我分成了四個三角形（教師引導學生感受從邊上任意一點出發分割），180°×4=720°。

師：現在出現了兩種結果，有沒有和這兩種都不一樣的了？

生：沒有了。

師：讓我們分別請這兩種結果的一位同學作代表，帶著他們的圖展示給大家看一下，請大家仔細觀察，說說你的想法。

（投影展示，學生觀察）

生：我認為720°的錯了，他多算了角。

生：我也認為720°的錯了。

師：他多算了哪里的角呢？請學生上來指一指。

師：是的，他多算了邊上新出現的角，那我們只要再用720°-180°就可以得出五邊形的內角和是540°。

師：分法不同，角的變化情況就不同，要仔細靈活處理。

師：老師剛剛還看到有同學這樣（課件或投影，教師引導學生感受從圖形中間任一點到多邊形頂點連線分割）將多邊形分成了幾個三角形，你們看，又該怎樣處理呢？

生：他這樣分成5個三角形也可以，但中間多出了一個周角，要用 180°×5-360°=540°。

生：對，把中間多出來的角減掉。

師：分法不止一種，請仔細觀察“從任意一個頂點出發分割”、“ 從邊上任意一點出發分割”、“從圖形中間任一點到多邊形頂點連線分割”這三種分法，他們分別分了幾次？五邊形被分成了幾個三角形？你覺得哪一種分法在算五邊形內角和時更方便？（課件出示）

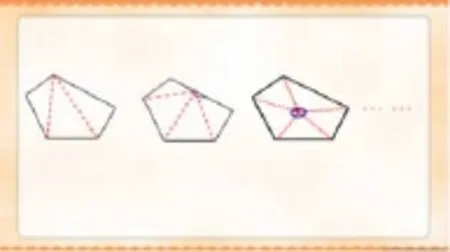
明確：從五邊形任意一個頂點出發，分別與它不相鄰的所有頂點（2個相對頂點）連線分最方便（不會產生新的角，只是將原來多邊形的內角進行了分割）。

師：請你分一分，求出六邊形的內角和。

（學生自主連線分割，求六邊形的內角和）

匯報交流并明確：

（課件出示）從六邊形任意一個頂點出發，分別與它不相鄰的3個相對頂點連線，將六邊形分割成4個三角形，則六邊形的內角和是180°×4=720°。

【評析：揭開四邊形的內角和這第一層面紗后，鼓勵學生自主遷移，從“任意一個頂點出發分割”、“邊上任意一點出發分割”、“圖形中間任一點出發分割”這三種分割角度重點對五邊形的內角和展開多維立體探究，進一步滲透數學思想。】

3.探究活動：探究其他多邊形的內角和，嘗試發現規律并小結明確。

師：讓我們繼續探究其他多邊形的內角和。請同學們從材料袋中選一個或自己畫一個多邊形（六邊形以上、小組內爭取不同圖形），求出它的內角和，并小組填寫“表格一”。

（學生自主探究填寫）

匯報交流：（板書）

七邊形 180°×5=900°

八邊形 180°×6=1080°

……

師：大家通過分割又快又好地求出了這些多邊形的內角和。接下來請大家再算算五十邊形的內角和。

（學生動手畫，又放棄）

師：大家怎么不動手了？

生：邊數太多，不好畫、分。

師：看來，碰上邊數較多的圖形，分割后算不是最好的方法，我們有必要來找找規律。請大家借助板書，小組完善“表格二”的填寫（課件出示“表格二”）。

（學生小組填寫表格）

集體交流，完善課件表格填寫。

?

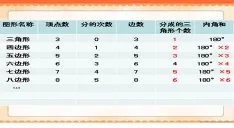
師：請大家仔細觀察表格中相關數據,看看能發現什么,在小組里說一說。

（學生觀察，小組交流）

集體匯報交流：

（1）多邊形的內角和與多邊形的頂點個數有關。

n邊形n個頂點，任意一個頂點有（n-3）個相對頂點，分（n-3）次，分成（n-3+1）個三角形，n邊形內角和為（n-3+1）×180°。

（2）多邊形的內角和與多邊形的邊數有關。

n邊形n條邊，分成（n-2）個三角形，多邊形內角和=（n-2）×180°。

4.立體切換，多維溝通。

師：用乘法分配律將多邊形的內角和公式變一變，（邊數-2）×180°=邊數×180°-2×180°=邊數×180°-360°（課件出示四邊形分割圖），你又有什么新發現？

說明：“從多邊形中間任一點出發分割”比“從多邊形任意一個頂點出發分割”總是多出一個周角，只要“邊數×180°-360°”即可求出多邊形的內角和。“從多邊形邊上任意一點出發分割”，只要“（邊數-1）×180°-180°”即可，（邊數-1）×180°-180°=邊數×180°-360°

【評析：把握數學本質，創設認知矛盾，激發規律探索需求，引領學生自發、自主探究規律，提升觀察、比較、歸納等多項能力。】

三、規律應用

師：現在你能求出五十邊形的內角和嗎？

生：（50-2）×180°=8640°。

師：n邊形呢？

生：（n-2）×180°。

師：一個多邊形內角和是1080°，你知道它是幾邊形嗎？

生：1080°÷180°+2=8，八邊形。

【評析：應用拓展，幫助學生進一步認識規律，培養運用意識及解決問題意識，提升解決問題的能力，發展核心素養。】

四、回顧感悟探究過程，文化鏈接

1.回顧感悟探究過程。

師：我們是怎樣探索發現多邊形內角和規律的？

師：回顧探究過程，你有什么收獲？

2.數學文化介紹。

（課件出示“古希臘數學家泰勒斯、歐幾里得等人多邊形內角和的探索歷程”簡介）

【評析：引領學生從知識探究過程本身、探究方法及數學思想等多個不同層面回顧感悟，再一次讓學生經歷探究規律活動的全過程，感悟規律探究的一般方法，提升素養并增加文化積累。】

五、總結提升

師：回顧本節課的學習，你有什么收獲？

（引導學生多角度說，相機小結提升）

師：我們的收獲不該止于某個規律、公式，掌握探究學習新知、發現規律的方法將會使我們受益終生。

【評析：引領學生多角度對整節課的學習進行回顧小結，培養反思總結能力，從重知識、規律的理解記憶轉變為重規律探究方法的感悟。】