采用數據包絡分析法的電力系統無功功率經濟優化問題研究
吳 亮,馬紹明,程鵬飛,張 鵬,范傳忠
(1. 國網鐵嶺供電公司,遼寧 鐵嶺 112000;2.國網撫順供電公司,遼寧 撫順 113000)
由于無功功率不適合遠距離大規模傳輸,因此系統中無功功率的補償是通過就地補償方式進行的,以此達到保持系統電壓穩定、降低有功功率損耗、減少設備無功補償費用的目的[1-4]。在以往無功優化問題研究中大部分是以有功功率損耗或電壓質量為優化目標,本文從機組運行無功傳輸經濟效率的角度出發,結合電網有功功率損耗作為優化目標函數之一,對電網無功功率進行優化計算。
數據包絡分析法[5-7](data envelopment analysis)是在相對效率基礎上發展起來的一種系統分析方法,它能夠快速準確評價被判客體的有效性及相對有效性,本文使用粒子群算法結合數據包絡分析方法對機組運行無功傳輸經濟效率進行分析,在滿足電網運行的條件下,達到全體機組運行無功傳輸經濟效率及網絡有功網損雙重最優化。
1 無功功率優化模型
無功功率過量傳輸會造成電網有功損耗的增加,因此無功功率優化可以減少系統有功功率損耗,本文提出以系統無功功率傳輸為變量,優化無功分布以達到電網有功功率損耗最小的優化模型見式(1):
(1)
式中:K為電網中變壓器支路的集合;ΔPi為第i臺變壓器支路上的有功功率損耗;G為電網中輸電線路的集合;ΔPj為第j條輸電線路上的有功功率損耗。
變壓器支路有功損耗為
(2)
輸電線路有功損耗為
(3)
式中:PiK為第i臺變壓器銅損;Pi為第i臺變壓器支路中傳輸的有功功率;Qi為第i臺變壓器支路中傳輸的無功功率;SiN為第i臺變壓器的額定容量;Pj為第j條線路中傳輸的有功功率;Qj為第j條線路中傳輸的無功功率;Vj為第j條線路額定電壓;Rj為第j條線路電阻。
等式約束為
(4)
(5)
式中:PGi和QGi、PDi和QDi、Vi為節點i注入功率有功和無功功率、有功和無功負荷、電壓幅值;Gij和Bij分別為節點i和節點j的互電導和互電納;Vj為支路j的電壓幅值;θij為節點i和節點j之間的相角差。
不等式約束為
PGmin≤PG≤PGmax
(6)
QGmin≤QG≤QGmax
(7)
QWmin≤Qk≤QWmax
(8)
VGmin≤VG≤VGmax
(9)
VLmin≤VL≤VLmax
(10)
SMmin≤SM≤SMmax
(11)
式中:PGmax、PGmin分別為發電機有功功率輸出的上下限約束值;QGmax、QGmin分別為發電機無功輸出的上下限約束值;QWmax、QWmin分別為無功補償裝置的上下限約束值;VGmax、VGmin分別為發電機電壓上下限;VLmax、VLmin分別為節點電壓上下限;SMmax、SMmin分別為線路傳輸功率上下限。
2 數據包絡分析法模型
在美國著名的運籌學家A.Charnes和W.W.Cooper創立數據包絡分析理論(DEA)以來,因為其具有所需要的指標少、不需要預先估算參數,而評價結果的靈敏性和可靠性高的特點被廣泛應用來評價對象運行的有效性和效率[8-9]。
在數據包絡分析理論中,被評價對象的特性是由決策單元決定的,每個決策單元都包含有相應的輸入量和輸出量。各個決策單元通過對輸入量和輸出量進行處理來實現對應的決策目標。
C2R模型是數據包絡分析理論中最主要也是目前應用最廣泛的模型,其主要內容如下。
設有n個決策單元,其中,第j個決策單元(xj,yj)的輸入量和輸出量分別為
xj=(xj1,xj2,…,xjk,…,xjn)
(12)
yj=(yj1,yj2,…,yjk,…,yjn)
(13)
對于第j0個決策單元,其輸入量、輸出量組成的單元設為(xj0,yj0)。
要對某個決策單元進行評價,就必須把各個輸入量和輸出量綜合成一個可以作為評價指標的數。
(14)
式(14)為決策單元評價指標表達式,其中:u=(u1,u2,…,un)為輸出量yj的權重系數;v=(v1,v2,…,vn)為輸入量xj的權重系數;Vp為評價指標。從式中可以看出,Vp≤1。Vp越接近1,輸入量xj對于輸出量yj來說就越有效,即xj被充分利用的程度就越高。當Vp等于1時,則輸入量xj與輸出量yj是最佳匹配關系,即達到系統評價的最優狀態。在被研究系統的歷史數據已知的情況下,(xj,yj)為已知量,u和v是未知量,因此提高Vp的辦法在于盡可能的改變u和v的值。所以構造C2R模型的目的在于量化u和v,使得Vp盡可能的接近1。經典C2R模型的表達式為
(15)
當引入新變量s+≥0.s-≥0時,則式(15)轉化為
(16)
式(16)為引入松弛變量s+、s-時的C2R對偶模型,是C2R模型廣泛使用的形式。式中,θ為當前被評價單元(x0,y0)的評價指標,反映其生產有效性。當θ越接近1時,評價單元(x0,y0)就越DEA有效。λj為輸入量和輸出量的權重,可以通過改變不同的權重值使得θ接近或者達到1。s+、s-為松弛變量,分別表示輸出的不足量和輸入的多余量。只有當θ=1且s+、s-都為0時,被評價單元才是絕對DEA有效的;否則僅當θ=1但s+、s-不都為0時,被評價單元為相對DEA有效,0<θ<1時,被評價單元為DEA無效,但隨著DEA指標越接近1,被評價單位有效性越好。
在C2R對偶模型中,DEA有效指的是對應決策單元的綜合有效性,綜合有效性包含規模有效和技術有效。規模有效性指的是隨著投入輸入量的繼續增多,則相應的輸出量也在增多而不是減少;技術有效性指的是在投入同等的輸入量,技術有效性高的可以獲得更多的輸出量或者是在同等產出的情況下,技術有效性高的可以投入更少的輸入量。
3 基于粒子群算法和數據包絡分析法(DEA)的無功功率多目標優化模型
3.1 粒子群算法
由于粒子群算法所需參數少,具有良好的尋找全局最優解的能力,也可有效避免算法早熟,因此本文采用粒子群算法求解電力系統無功優化問題[10-11]。
在粒子群算法中,假設解空間為n維空間。設xi=(xi,1,xi,2,xi,3,…,xi,n)為第i個粒子的位置,vi=(vi,1,vi,2,vi,3,…,vi,n)為第i個粒子的速度;pi=(pi,1,pi,2,pi,3,…,pi,n)為第i個粒子的歷史最好位置。
vi,j(t+1)=wvi,j(t)+c1r1[pi,j-xi,j(t)]+c2r2[pg,j-xi,j(t)]
(17)
xi,j(t+1)=xi,j(t)+vi,j(t+1)
(18)
式中:w為慣性因子,決定著算法的搜索能力;c1、c2為學習因子,c1決定著粒子自身信息的傳承,c2決定著粒子與整個群落信息的交換;r1和r2為[0,1]之間的滿足均勻分布的隨機數,決定著算法在全局搜索和局部搜索上的性能;xi,j(t)為第i個粒子的第j維在進行第t次迭代時在解空間所處的位置;pi,j為第i個粒子的第j維在以往迭代過程中產生的最好位置;pg,j為整個群落在第j維上的最好位置;xi,j(t+1)為第i個粒子的第j維在進行第t+1次迭代時在解空間所處的位置;vi,j(t+1)為第i個粒子的第j維在t+1次迭代時的移動速度矢量。
3.2 基于粒子群算法和數據包絡分析法(DEA)的無功功率多目標優化計算模型
本文以式(1)作為目標函數之一;將系統內各機組作為數據包絡分析的決策單元,同時以機組無功出力作為決策單元的輸入量,以經潮流計算所得各節點電壓與標準電壓之間偏移量作為輸出量,以式(14)做為另1個目標函數搭建無功功率多目標優化模型,約束條件為式(4)—(11)及式(16)所示。
4 實例計算分析
本文以IEEE14節點系統為例進行計算,算法參數設置:初始種群設為20;w=0.6:學習因子c1=0.75,c2=1.0,最大迭代次為1 500次,計算結果見表1、表2。
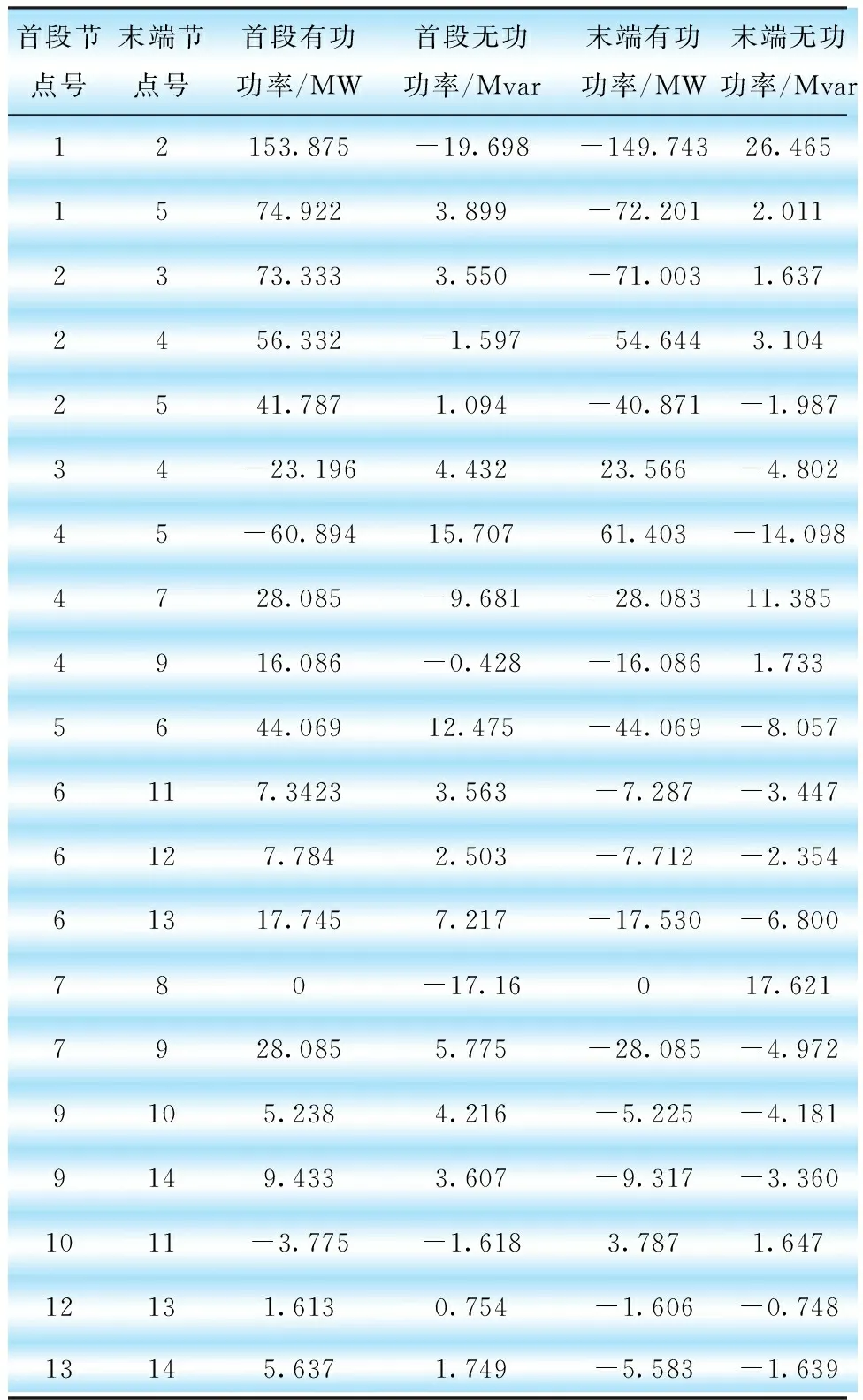
表1 IEEE14節點系統初始潮流結果
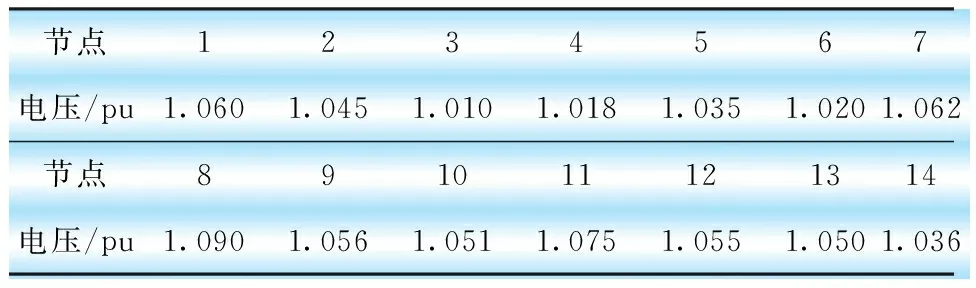
表2 IEEE14節點系統初始各節點電壓計算結果
經過粒子群算法和數據包絡分析法的無功功率多目標優化計算,計算結果見表3、表4。
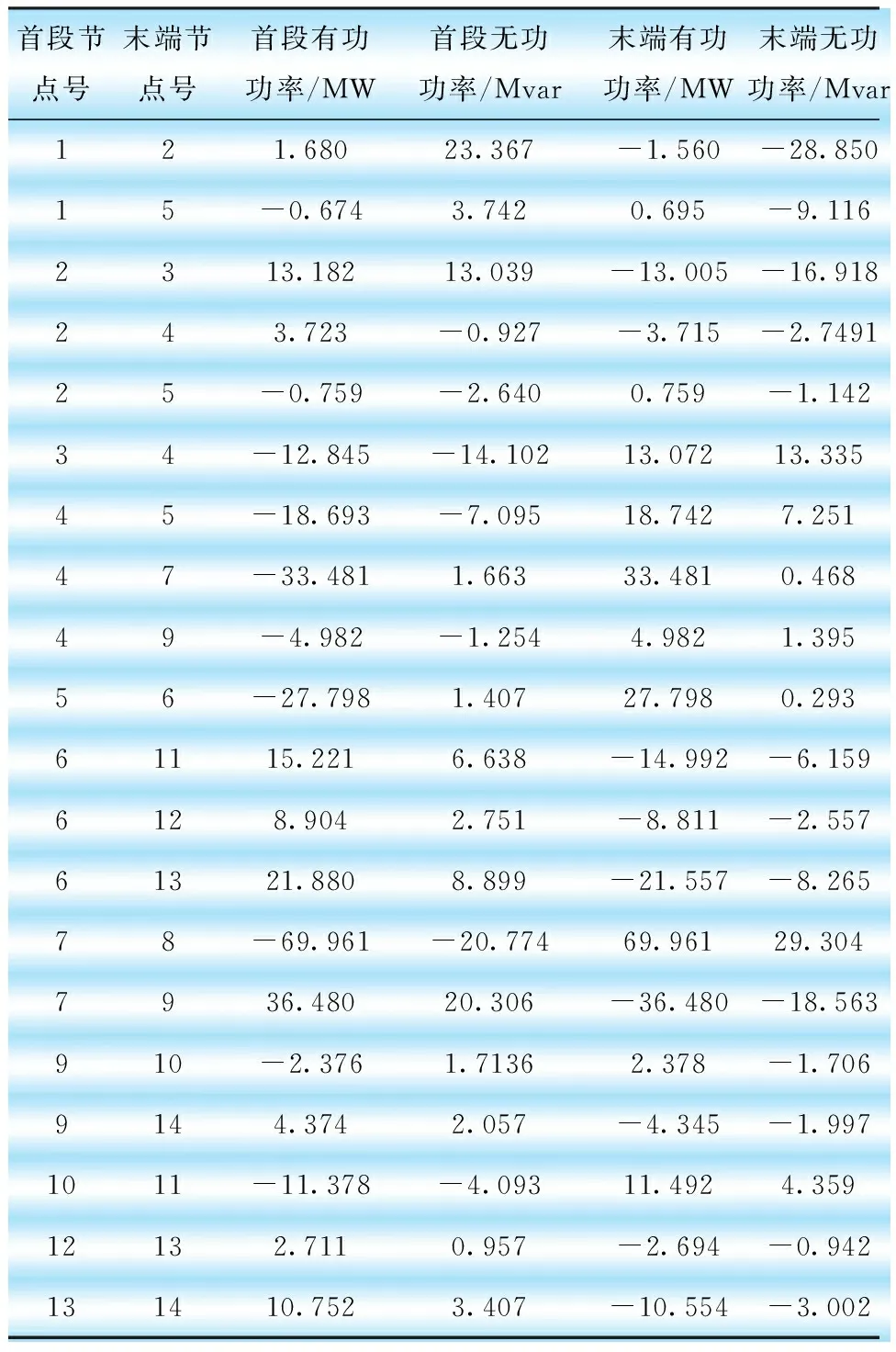
表3 IEEE14節點系統潮流優化結果
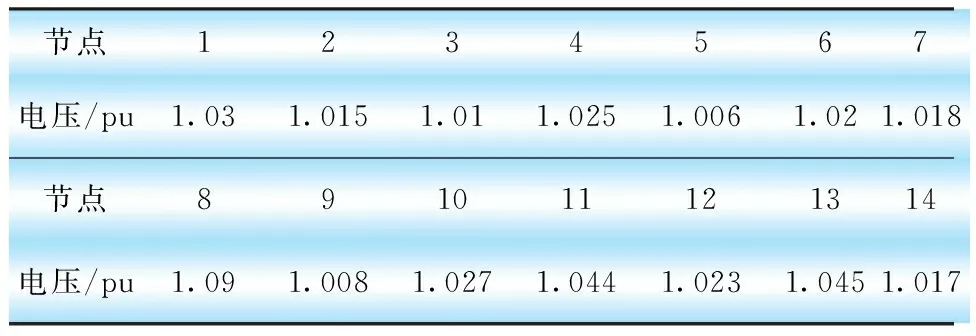
表4 IEEE14節點系統各節點電壓優化計算結果
IEEE14節點系統原始潮流無功損耗約為54.54 Mvar,經過優化后系統無功損耗約為17.79 Mvar,經對比可知,無功損耗減少36.75 Mvar,網絡中無功損耗情況得到很大的改觀。原始數據IEEE14系統有功損耗約為13.393 MW,經過優化后有功系統損耗約為1.482 MW,經過對比,有功損耗減少11.911 MW,有功損耗也相應降低。
由表5和表6可知,表5中機組2、表6中機組3和機組4的DEA有效值θ均達到1,表明其機組運行經濟效率最高,其余機組的DEA有效性指標θ均不為1,DEA有效值低于1表明經濟效率有待提高。機組DEA有效值越接近1,其機組運行的經濟效率越高,對系統而言機組的運行潛力開發越高。通過本文數據包絡分析進行計算后可得知,在已經經過優化的電網中,機組3和機組4的經濟運行效率得到充分開發,電力公司調整發電曲線時可從機組3和機組4著手,從而最大限度提高電網運行經濟效率。
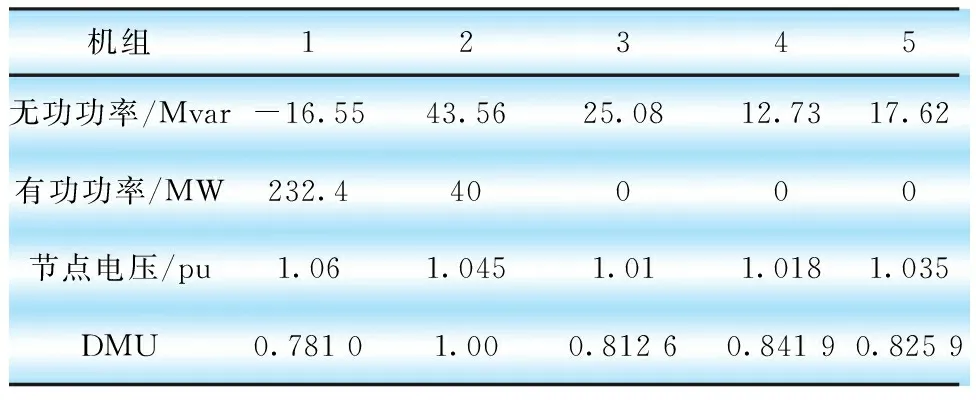
表5 初始機組數據包絡分析指標

表6 優化后機組數據包絡分析指標
5 結束語
針對傳統的解決無功功率優化問題時集中關注于系統有功損耗最小的情況,本文通過采用粒子群算法和數據包絡分析方法對系統無功功率進行優化,從提高機組運行無功經濟效率的角度出發,將提高機組運行無功傳輸經濟效率與降低有功損耗并重,通過算例證明本文所提方法在降低系統有功損耗和提高機組運行無功傳輸經濟效率方面具有雙重指導意義。
參考文獻:
[1] 郝思鵬,王正風.電力市場下的無功定價研究[J].繼電器,2006,34(19):51-54.
[2] 代紅才,彭建春,楊幫宇,等.基于邊際成本和潮流追蹤的無功定價[J].電網技術,2007,31(7):59-63.
[3] 張勇軍,任 震,李邦峰.電力系統無功優化調度研究綜述[J].電網技術,2005,29(2):50-56.
[4] 岳 青,魏宇存,孫 蕾,等.榆林電網無功優化運行研究[J].電工電氣,2012, 3(3):21-25.
[5] 魏權齡.數據包絡分析(DEA)[J].科學通報,2000,45 (17):1 793-1 808.
[6] 羅道平,肖 笛.數據包絡分析(DEA)在電力工業的應用[J].系統工程理論與實踐,1996, 4(4):60-66,112.
[7] 樓旭明,竇彩蘭,汪貴浦.基于DEA的中國電力改革績效相對有效性評價[J].當代財經,2006,4(4):90-93.
[8] 解百臣,吳育華.基于SE-DEA的電力企業效率評估[J].電子科技大學學報(社科版),2005,7(4):25-27.
[9] 朱春波. DEA在電網企業投入產出績效評價中的應用研究[D]. 重慶:重慶大學,2008.
[10] 曾嘉俊,劉志剛,何士玉,等.一種基于子區域粒子群的無功優化算法研究[J].電力系統保護與控制,2012,40 (1):37-42.
[11] 侯云鶴,魯麗娟,熊信艮,等.改進粒子群算法及其在電力系統經濟負荷分配中的應用[J].中國電機工程學報,2004,24(7):99-104.

