統計的思想方法
渠 英
我們的生活、工作離不開數據,要做到心中有數、用數據說話是信息社會對人的基本要求.因此,收集、整理、分析數據,并在此基礎上做出推斷就是必不可少的步驟了.而隨機抽樣與統計推斷是最重要的一環.我們要善于利用樣本的某種特征去估計總體的相應特征,用樣本的平均水平、波動情況、分布規律等特征估計總體的平均水平、波動情況和分布規律,根據統計結果做出判斷和預測.
例1 為了解某水果批發市場荔枝的銷售情況,某部門對該市場的三種荔枝A、B、C在6月上半月的銷售進行調查統計,繪制成如下兩個統計圖(均不完整).請你結合圖中的信息,解答下列問題:
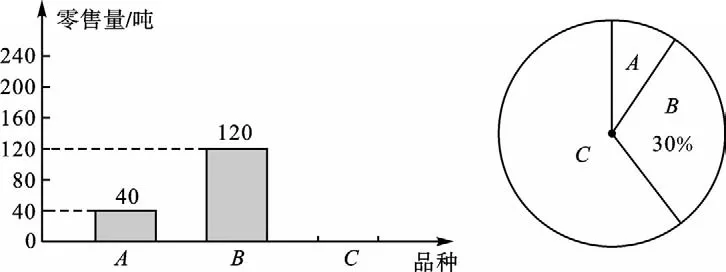

(1)該市場6月上半月共銷售這三種荔枝多少噸?
(2)該市場某商場計劃六月下半月進貨A、B、C三種荔枝共500噸,根據該市場6月上半月的銷售情況,求該商場應購進C品種荔枝多少噸比較合理?
【分析】(1)根據B品種有120噸,占30%即可求得調查的這三種荔枝的總噸數;(2)總數量乘C品種荔枝所占的百分比,即可求出應購C類品種數量.
解:(1)120÷30%=400(噸).
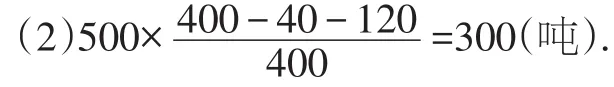
【點評】本題考查的是條形統計圖和扇形統計圖的綜合運用,讀懂統計圖,從不同的統計圖中得到必要的信息是解決問題的關鍵.條形統計圖能清楚地展示出每個項目的數據;扇形統計圖直接反映部分占總體的百分比大小.運用數學知識解決實際問題的過程是:從實際問題中獲取必要的信息——分析處理有關信息——建立數學模型——解決這個數學問題.利用圖表獲取數據信息,收集、整理分析數據,再運用統計量的意義去分析,這是用統計的思想方法解決問題的基本方式.
例2 為了幫助九年級學生做好體育考試項目的選考工作,某校統計了本縣上屆九年級畢業生體育考試各個項目參加的男、女生人數及平均成績,并繪制成兩個統計圖如下圖,請結合統計圖信息解決問題.

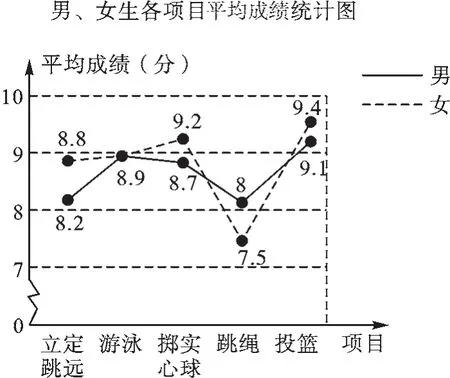
(1)“擲實心球”項目男、女生總人數是“跳繩”項目男、女生總人數的2倍,求“跳繩”項目的女生人數;
(2)若一個考試項目的男、女生總平均成績不小于9分為“優秀”,試判斷該縣上屆畢業生的考試項目中平均成績達到“優秀”的有哪些項目,并說明理由;
(3)請結合統計圖信息和實際情況,給該校九年級學生體育考試項目的選擇提出合理化建議.
【分析】(1)根據統計圖得到“擲實心球”項目男、女生總人數為1000名,“擲實心球”項目男、女生總人數是“跳繩”項目男、女生總人數的2倍,可求出“跳繩”項目男、女生總人數為500名,因為男生人數為260名,所以“跳繩”項目的女生人數為240名;(2)根據男、女生各項目平均成績統計圖計算出“優秀”的項目;(3)根據統計圖提出合理化建議,合理即可.
解:(1)(400+600)÷2-260=240(人).
(2)觀察男、女生各項目平均成績統計圖可知:“立定跳遠”“游泳”“跳繩”三項目的男、女生平均成績均小于9分,所以男、女生總平均成績也小于9分;“投籃”項目的男、女生平均成績都大于9分,所以男、女生總平均成績也大于9分;“擲實心球”項目的男、女生總平均成績為=9分,所以屬于“優秀”項目的有“投籃”“擲實心球”兩個項目.
(3)基于上屆畢業生的體育成績和學生的身體素質以及市體育優秀標準,可選“投籃”,人數雖然不是最多,但平均成績較高,所以建議選“投籃”;“游泳”項目考試的人數最多,平均成績接近9分,故也可以選考“游泳”.“跳繩”項目的報名人數少且平均成績又低,若不是跳繩水平很高,建議不選該項目.
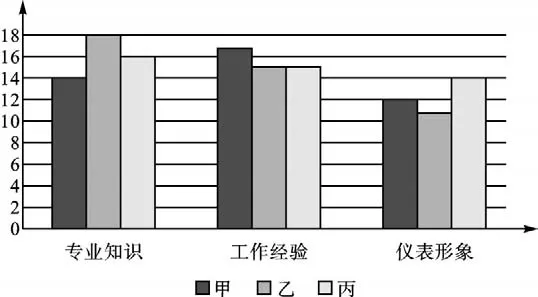
例3 某集團公司對應聘者甲、乙、丙進行面試,并從專業知識、工作經驗、儀表形象三方面給應聘者打分,每一方面滿分20分,最后的打分制成條形統計圖(如圖).
(1)利用圖中提供的信息,在專業知識方面3人得分的極差是多少?在工作經驗方面3人得分的眾數是多少?在儀表形象方面3人誰最有優勢?
(2)如果專業知識、工作經驗、儀表形象三個方面的重要性之比為10∶7∶3,那么作為人事主管,你應該錄用哪一位應聘者?為什么?
(3)在(2)的條件下,你對落聘者有何建議?
【分析】(1)一組數據中,最大值與最小值的差叫極差,眾數是一組數據中出現次數最多的數,有時一組數據中的眾數不止一個,有時沒有眾數,某項中得分最高者最有優勢;(2)根據3人的各項得分占的比算出總分,高者被錄用;(3)根據統計計算結果,做出合理的判斷,較清楚表達自己的觀點.
解:(1)專業知識方面3人得分分別為14分、18分、16分,所以,極差是18-14=4;在工作經驗方面,3人得分分別是17分、15分、15分,所以眾數是15;在儀表形象方面3人得分分別為12分、11分、14分,所以丙最有優勢.

乙得分最高,所以乙被錄用.
(3)建議例如:對甲而言,應加強專業知識的學習,同時要注意自己的儀表形象;對丙而言,三方面都要努力,重點在專業知識和工作經驗.
【點評】一組數據從不同的角度出發,常常會有不同的結論,在我們生活中,評選先進、選拔人才等,會因不同的權重,得出迥異的結果.可見我們要妥善安排,使權重盡量合理,以突出重點,優劣得當.
例4 為吸引更多更好的初中畢業生報考,某校在招生廣告上大力宣傳該校近年來的辦學成就,并制作了近五年該校高中畢業生升入大學的人數統計圖.
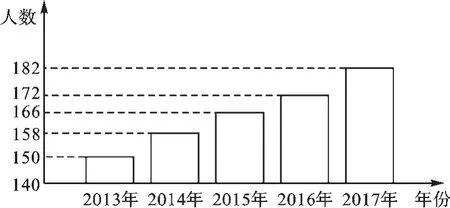
(1)你認為該校制作的統計圖是否存在誤導的成分?
(2)“升入大學的人數”與“升入大學的人數占當年學校畢業生總人數的比例”這兩個統計量中哪個更能說明問題?
(3)作為一名初中畢業生,如果你打算報考該校,那么你認為還需了解哪些信息以便使你做出正確的決策?
【分析】這是一個容易引起誤導決策的統計圖,雖然看起來升學人數一路攀升,但是這個攀升是在怎樣的背景下產生的?高中、大學招生人數是年年在大幅度增加還是在減少?
解:(1)學校只統計了每年升入大學的人數,而沒有統計當年的畢業生總人數,所以存在誤導.
(2)選用“升入大學的學生數占當年學校畢業生數的比例”這一統計量顯然比“升入大學的人數”更合理.
(3)還需了解每年同期其他學校升入大學的學生數占當年學校畢業生數的比例、近幾年大學是否存在“大規模擴招”等現象;還可了解該校每屆畢業生當年入學時的總體成績情況以便與畢業時高考成績作比較.
【點評】本題是一道分析廣告信息是否合理性的實際問題,面對廣告數據,我們應全面分析,才能做出決策.

