待定系數法在初中數學中的應用
吳 琴

對于某些數學問題,如果已知所求結果具有某種確定的形式,則可引進一些尚待確定的系數來表示這種結果,通過已知條件建立起給定的算式和結果之間的關系式,得到以待定系數為元的方程或方程組,解得待定系數,從而使問題得以解決,這個方法叫待定系數法.此法在初中數學中有著廣泛的應用,下面舉例予以說明.
一、函數方面的應用
待定系數法最常見的就是在函數方面的應用,用以確定函數表達式.主要原因就是不管是一次函數、反比例函數還是二次函數都有其固定的形式,這為建立方程(組)提供了依據.
例1 已知二次函數的圖像經過點(-1,-6)、(1,-2)和(2,3).求這個二次函數的關系式.
【分析】因為題中給的是圖像過三個普通點,所以應該設二次函數的一般形式y=ax2+bx+c(a,b,c為常數,a≠0),接著將點的橫、縱坐標代入函數表達式,求出a,b,c的值.
解:設二次函數的解析式為y=ax2+bx+c(a,b,c為常數,a≠0),
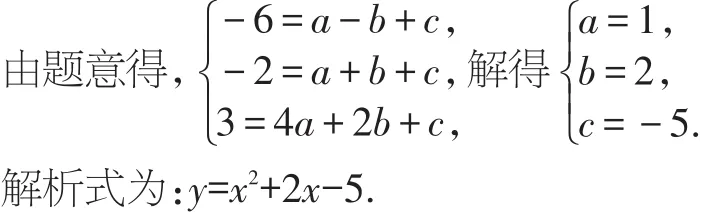
【點評】本題主要考查的是如何用待定系數法確定函數的表達式,正確解答此題的關鍵是設出函數的一般形式,代入點的坐標,得到方程組,求出系數,即可求出函數表達式.
例2 已知關于x的一次函數y=kx+b的圖像平行于直線y=-3x+4,且其圖像經過點(3,0),求此一次函數的解析式.
【分析】兩個一次函數的圖像互相平行,即k的值相同.
解:因為一次函數y=kx+b的圖像平行于直線y=-3x+4,所以k=-3,所求一次函數為y=-3x+b,
把x=3,y=0代入y=-3x+b中得0=-9+b,
∴b=9,
∴一次函數的解析式為y=-3x+9.
【點評】若一次函數y=k1x+b1與y=k2x+b2的圖像互相平行,則k1=k2且b1≠b2.故求一次函數的解析式時,可先直接求出k的值,再找一個條件求出b的值即可.兩個圖像(直線)平移也屬互相平行關系.
二、因式分解中的應用
例3 如果x3+ax2+bx+8有兩個因式x+1和x+2,則a+b=( ).
A.7 B.8 C.15 D.21
【分析】原多項式必能分解為三個一次因式的積,第三個因式應該是形如x+c的一次二項式,故可以考慮用待定系數法求解本題.
解:可設x3+ax2+bx+8=(x+1)(x+2)(x+c),展開等號右邊部分得x3+ax2+bx+8=x3+(3+c)x2+(2+3c)x+2c,比較系數,

a+b=21,故選D.
【點評】本題主要考查因式分解的概念,解決本題的關鍵是利用代數恒等式的定義,系數對應相等,從而求出待定的系數.
例4 分解因式x4+x3+4x2-3x+5.
【分析】這是一個關于x的四次多項式,可考慮用待定系數法分解成兩個二次三項式的乘積.
解:設x4+x3+4x2-3x+5
=(x2+ax+1)(x2+bx+5)
=x4+(a+b)x3+(ab+6)x2+(5a+b)x+5,
比較等式兩邊同次項的系數,

由①③式確定a=-1,b=2,代入②成立,
∴x4+x3+4x2-3x+5=(x2-x+1)(x2+2x+5).
【點評】在上述過程中,又因為5=(-1)×(-5),若設原式=(x2+ax-1)(x2+bx-5),則得到關于a,b的方程組無解.故運用待定系數法時,有時需要用計算來排除某種分解不可能的情況.
三、用于拆分分式

【點評】本題主要考查將一個分式分成幾個分式的和.解決本題首先應將分母去掉,這樣形式上會簡單很多,然后等號兩邊分別整理,利用代數恒等式的定義,得到關于系數的方程組,從而求出待定系數的值.
綜上,待定系數法實質上是一種求未知系數的方法.經常將一個多項式表示成另一種含有待定系數的新的形式,這樣就得到一個代數恒等式.然后根據代數恒等式的性質得出系數應滿足的方程或方程組,其后通過解方程或方程組便可求出待定的系數,或找出某些系數所滿足的關系式.

