歸納猜想見微知著

孔雙玉

歸納猜想型問題也是規律探索型問題，主要有“數、式、圖形”等類型，對同學們的觀察、歸納、分析及推理能力要求較高，經常以選擇、填空、壓軸題的形式出現.我們常用的解析模式是“特殊—一般—特殊”，這也是人類認識新生事物的一般規律.歸納猜想有利于培養創造性思維能力，是學習初中數學知識所必備的數學核心素養之一.下面讓我們一起在相關問題的解析中，感受“歸納猜想”的魅力.

一、歸納數式的變化規律

例1 觀察下列等式：

第1層 1+2=3

第2層 4+5+6=7+8

第3層 9+10+11+12=13+14+15

第4層 16+17+18+19+20=21+22+23+24

……

在上述數字寶塔中，從上往下數，數字2016在第 層.

【分析】本題的塔狀數式規律看似明顯，同學們往往抓不住觀察的“要點”，而兩端數據的規律發現，則是本題的突破口，不同視角的觀察、歸納、猜想，也成就了數學的趣味性.

解：由觀察可知：

1=12；4=22；9=32；16=42；…

經計算，易知442＜2016＜452

所以2016在第44層.

【點評】數學源于自然，在貌似平常的自然現象中蘊含的數學規律，能讓我們感受到數學的奇妙與魅力，這也是中考命題的源泉.

例2 把所有正奇數從小到大排列，并按如下規律分組：（1），（3，5，7），（9，11，13，15，17），（19，21，23，25，27，29，31），…，現有等式Am=（i，j）表示正奇數m是第i組第j個數（從左往右數），如A7=（2，3），則A2015=（ ）.

A.（31，50）B.（32，47）

C.（33，46）D.（34，42）

【分析】本題考查同學們對于數據的次序及個數的準確認知.我們首先要認清數據在數軸上的數點表示，而且要對等差數列求和的相關知識有所了解，并能夠準確應用.

解：令2n-1=2015，解得n=1008，

經計算，易知 312＜1008＜322，所以1008-312=47.

綜上可知，A2015=（32，47）.

【點評】要想準確快速地解決此類問題，必需有意識地培養數學思維的層次性，從數點和數列求和的不同視角審視問題，積累等差數列相關的性質、運算技巧，同時為高中數學的學習打下堅實的基礎.

二、歸納圖形的變化規律

例3 如圖1，已知直角三角形ACB，AC=3，BC=4，過直角頂點C作CA1⊥AB，垂足為A1，再過 A1作 A1C1⊥BC，垂足為 C1；過 C1作 C1A2⊥AB，垂足為 A2，再過 A2作 A2C2⊥BC，垂足為C2……這樣一直作下去，得到一組線段：CA1，A1C1，C1A2……則第10條線段A5C5= .

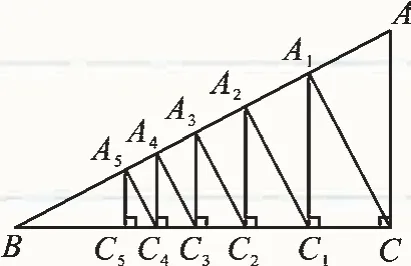
圖1

【分析】直角三角形相關知識是中考數學考查的重點，尤其像這種垂直線段的迭代關系，一定要著眼于抓住變化中的“不變量”，加以歸納、運用.

在Rt△AA1C中，易知A1C=3sinA，

【點評】直角三角形中銳角三角函數的靈活運用是中考的熱點問題，在迭代規律的應用中，要及時觀察歸納數據規律，并加以合理的猜想運用，這會讓我們體會到數學的簡約之美、應用之美.

例4 如圖2，對面積為1的△ABC逐次進行以下操作：第一次操作，分別延長AB、BC、CA 至點 A1、B1、C1，得到 A1B=2AB，B1C=2BC，C1A=2CA.順次連接 A1、B1、C1，得到△A1B1C1，記其面積為S1；第二次操作，分別延長A1B1、B1C1、C1A1至 點 A2、B2、C2，使 得 A2B1=2A1B1，B2C1=2B1C1，C2A1=2C1A1，順次連接 A2、B2、C2，得到△A2B2C2，記其面積為S2……按此規律繼續下去，可得到△A5B5C5，則其面積S5=_____.

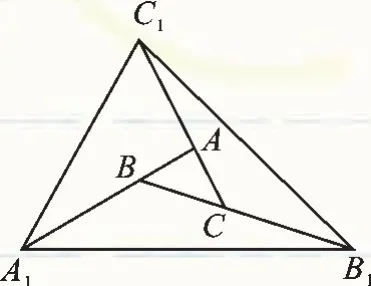
圖2

【分析】本題考查同學們的觀察發現能力，以及對于三角形面積比例問題的敏銳性.易錯點在于，誤認為是三角形的相似變化，實則不然，需要運用輔助線分割處理，才能歸納出迭代操作中面積的變化規律.

解：連接A1C，

由A1B=2AB，B1C=2BC，C1A=2CA，

【點評】迭代操作問題的解決，關鍵在于每一次操作后圖形變化規律的發現、歸納；同時，平面幾何問題的解決也往往需要輔助線的幫助.

三.歸納坐標的變化規律

例5點B（11，y1）、B（22，y2）、…、B（nn，yn）（n是正整數）依次為一次函數y=x+圖像上的點，如圖4，已知點A（1x1，0）、A（2x2，0）、…、A（nxn，0）（n是正整數）依次為x軸正半軸上的點，已知x1=a（0＜a＜1），△A1B1A2、△A2B2A3、△A3B3A4、…、△AnBnAn+1分別是以B1、B2、B3、…、Bn為頂點的等腰三角形.

圖4

（1）寫出B2、Bn兩點的坐標.

（2）求x2、x（3用含a的代數式表示）；分析圖形中各等腰三角形底邊長度之間的關系，寫出你認為成立的兩個結論.

（3）當a（0＜a＜1）變化時，在上述所有的等腰三角形中，是否存在直角三角形？若存在，求出相應的a的值；若不存在，請說明理由.

【分析】本題主要考查初等函數的應用及觀察、歸納、分析論證的綜合能力，尤其是奇數位置、偶數位置上等腰三角形底邊長規律的發現，是解析問題的突破口.

解：（1）因為點 B2，Bn在直線 y=x+上，且橫坐標分別為2，n，

（2）由等腰三角形“三線合一”的性質及數軸上兩點間距離的概念，易知：

x2=1+（1-a）=2-a，

x3=2+［2-（2-a）］=2+a.

結論 1：頂點為 B1，B3，B5…這些奇數位置上的等腰三角形底邊的長都等于2-2a；

結論 2：頂點為 B2，B4，B6…這些偶數位置上的等腰三角形底邊的長都等于2a；

結論3：每相鄰的兩個等腰三角形底邊之和都等于常數2.

（3）設第n個等腰三角形恰好是直角三角形，則這個三角形的底邊長等于高yn的2倍.

由（2）知：①當n為奇數時，有

綜上所述，存在等腰直角三角形.當a=時，第一個三角形是等腰三角形；當a=時，第二個三角形是等腰直角三角形；當a=時，第三個三角形是等腰直角三角形.

【點評】面對函數情境中坐標的變化，問題解決的關鍵點在于等腰三角形底邊長度規律的歸納、猜想及應用，其次才是n范圍的限定求值.