1200 MW級汽輪發電機定子繞組端部模態分析

陳力飛，吳新亞，董興建，彭志科，孟 光

（1.上海交通大學 機械系統與振動國家重點實驗室 振動、沖擊、噪聲研究所，上海 200240；2.上海電氣電站設備有限公司 發電機廠，上海 200240）

大型汽輪發電機運行過程中，定子端部受二倍工頻(即100 Hz)的電磁激振力。如果定子端部的模態頻率接近100 Hz，將發生諧振，從而可能因振幅過大而發生結構件松動、磨損、絕緣損壞等現象，影響汽輪發電機的正常運行，甚至造成重大事故[1]。

根據GB/T20140-2016《隱極同步發電定子繞組端部動態特性和振動測量方法及評定》，在汽輪發電機的設計中須根據定子端部的模態特性進行結構優化，以使其模態頻率避開95 Hz～110 Hz。為此，針對定子端部的模型建立與模態計算，學者們開展了持續深入的研究。黃偉、趙清等認為錐環與定位支架之間是固定的，采用MPC綁定實現定位支架與錐環的連接，以此建立定子端部有限元模型，通過實驗進行驗證并分析誤差來源[2–3]。楊昔科等分別利用梁單元和實體單元建立了線棒和膠體，對灌注式汽輪發電機定子繞組端部結構進行了分步有限元仿真模態分析，修正了仿真模型的關鍵參數[4]。王益軒等將定子端部及其支撐部分簡化成均勻連續的錐殼及旋轉對稱薄板組合結構，對模型的材料參數和幾何參數進行動態優化設計[5–6]。

然而，在目前的研究工作中，存在著三個問題。第一，處理邊界條件時將定位支架與錐環作綁定約束，在實際工況下，定位支架與錐環是接觸關系，會發生相對滑動，將這兩部分直接綁定連接會帶來誤差[7]；第二，采用梁單元建立線棒的建模方式必須通過MPC綁定將線棒與膠體連接，這種連接方式使線棒-膠體結構的模型整體動力特性與實際結構相比有很大的偏差；第三，在有關模型的優化設計的工作中，采用的模型過于簡化，優化結果精確性不高。

針對當前研究的不足，以1200 MW灌注式汽輪發電機定子繞組端部為研究對象，提出了一種線棒-膠體的均勻化等效建模方法，以降低其建模難度并提高精度，基于接觸靜力學分析確定定位支架與錐環之間的等效剛度，通過靈敏度分析明確影響汽輪發電機定子端部模態的關鍵因素，為定子端部的結構設計提供指導意見。

1 定子端部結構特征及錐環的簡化

1.1 端部結構特征

如圖1，灌注式汽輪發電機定子繞組端部主要由鐵心、錐環、線棒-膠體、壓圈、壓板、絕緣拉桿及定位支架等部分組成。定位支架焊接在鐵心上，錐環通過定位支架安裝在鐵心上。

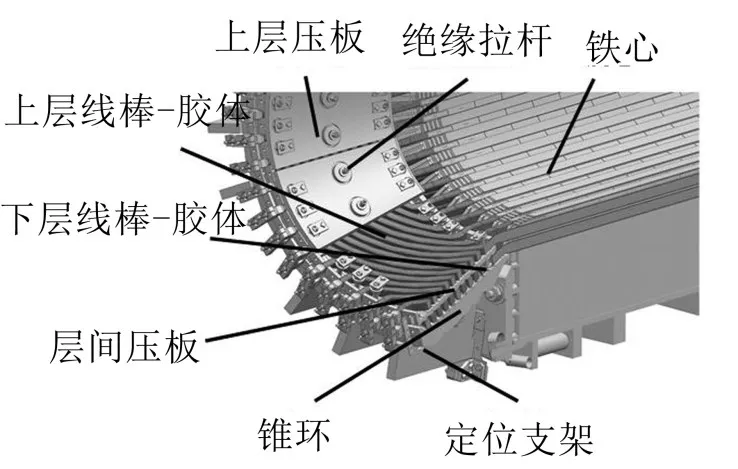
圖1 汽輪發電機定子繞組端部模型

線棒又稱繞組，分為上下兩層。線棒外圍灌注室溫固化樹脂膠體，形成線棒-膠體結構。絕緣拉桿將層間壓板、上層壓板以及線棒-膠體結構壓緊并固定在錐環上，使發電機定子繞組端部成為一個整體，具有很強的剛度[8]。

1.2 錐環的簡化模型

錐環是發電機定子繞組端部結構的重要組成部分，由浸漬熱態高性能環氧樹脂的玻璃纖維材料纏繞而成。如圖2所示，根據纖維材料的編織方向，錐環可以分成內層和外層。內層材料由纖維沿著表面±45度交叉纏繞而成，外層材料由纖維沿著周向纏繞而成，具體材料參數如表1。

表1 錐環內外層材料參數

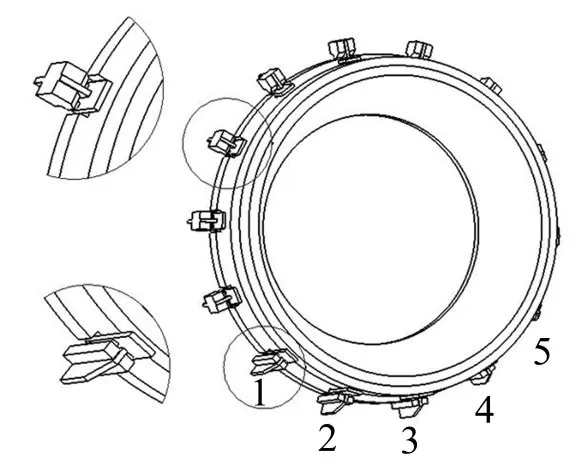
圖2 錐環模型

忽略錐環結構中的螺孔和凹槽，建立其有限元模型。對錐環結構分別進行了實驗模態分析和有限元模態分析，前兩階模態的頻率如表2所示。

表2 錐環模態實驗結果與仿真結果對比

與實驗結果相比，仿真結果的前2階模態頻率誤差都小于3%，認為錐環有限元模型足夠精確。

2 定位支架與錐環的接觸剛度

錐環與定位支架之間是接觸關系，在模態分析中無法模擬接觸邊界條件。為此，擬通過接觸靜力學計算獲得錐環與定位支架的接觸剛度，用彈簧單元表征接觸剛度，近似模擬接觸邊界條件。如圖3。錐環下方1－5號定位支架為完全相同的承重支架，其它定位支架為非承重支架。實驗表明，非承重支架的剛度遠小于承重支架，因此忽略非承重支架的剛度。

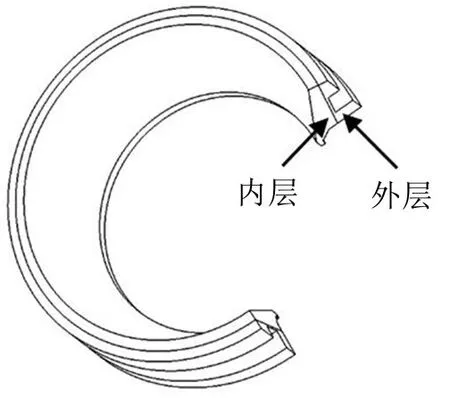
圖3 錐環支架示意圖

采用接觸靜力學分析方法確定單個承重支架的等效剛度。建立承重支架的有限元模型，在其上方建立與錐環表面曲率相同的弧形板以模擬承重支架與錐環的接觸關系。在承重支架的上表面用TARGE170建立目標單元，弧形板下表面用CONTA174建立接觸單元，通過面-面接觸方式實現弧形板和承重支架的接觸，設摩擦系數為0.2，接觸剛度系數FKN為默認值1.0。通過對弧形板施加不同大小的壓力，計算得到承重支架上表面的位移量與對應受力大小的關系，從而獲得支架在不同變形量情況下的剛度，具體結果如圖4。

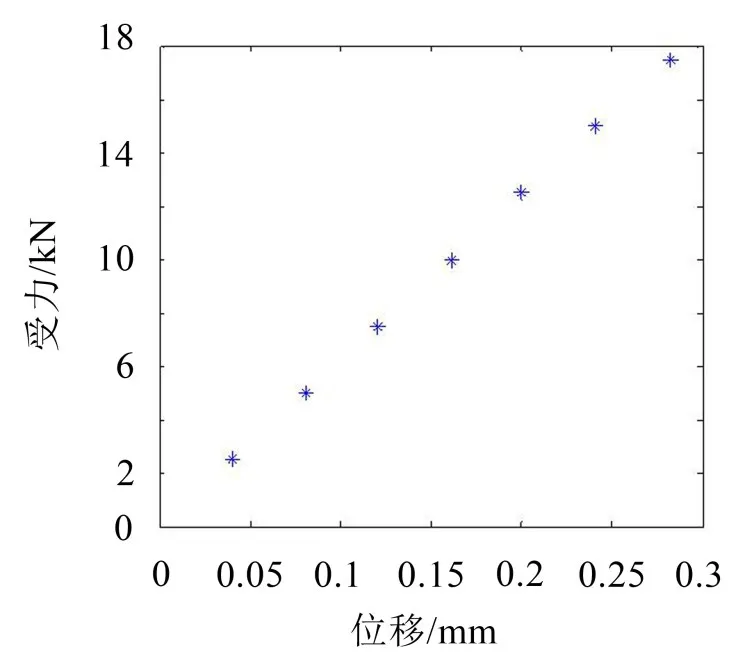
圖4 定位鍵支架受力變形圖

忽略鐵心的變形，將五個承重支架與鐵心焊接面的所有自由度固定，施加重力場使錐環的重力施加在承重支架上，單元的設置、摩擦系數的大小、接觸剛度系數FKN與單個承重支架的設置相同。通過靜力學分析，得到5個承重支架上表面的平均位移均在0.26 mm左右。

由圖4知，承重支架的位移為0.26 mm時，剛度約為6.22×104N/mm。在建立端部仿真模型時，用相同剛度的彈簧單元替換這些支架。

3 線棒-膠體結構的均勻化建模方法

3.1 線棒-膠體分區域建模策略

發電機端部線棒結構較為復雜，為漸開線結構，外圍通過灌注室溫固化樹脂膠體，形成線棒-膠體結構。目前，線棒-膠體結構的建模方式主要有兩種：一種是將線棒和膠體分別采用梁單元和殼單元進行建模，另一種是將線棒和膠體分別采用梁單元和實體單元進行建模，這兩種方法均無法將線棒和膠體的網格匹配起來，只能通過MPC將兩者綁定，導致線棒-膠體結構的模型整體動力特性與實際結構相比有很大的偏差。

考慮到上述兩種建模方式在節點耦合方面的問題，采用將線棒-膠體等效均勻化的建模策略，把復雜的線棒-膠體結構等效成由正交各向異性材料建立的均勻實體單元錐環型結構，通過等效材料的材料參數和主軸方向來體現線棒-膠體結構的結構特性，降低了建模難度并提高了精度。

如圖5所示，根據端部線棒的走向，將一層線棒-膠體分成3個區域，每個區域中線棒和膠體的體積比不同。

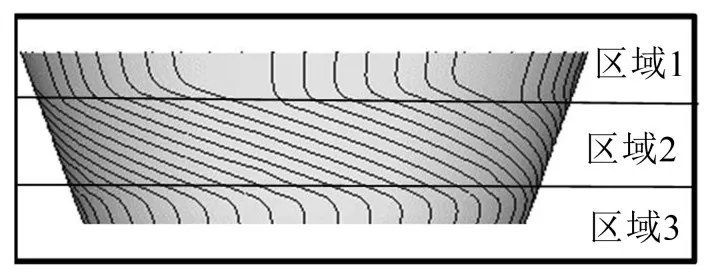
圖5 “線棒-膠體”分塊示意圖

簡化起見，將每個區域等效為均勻的正交各向異性材料，每個區域的材料參數和材料主軸方向均不一樣。利用solid186單元的層合功能控制每個區域材料的主軸方向。采用優化算法得到不同體積比下的線棒-膠體材料參數。

3.2 線板-膠體材料的均勻化方法

（a）優化方法的原理及目標函數

如圖6，采用實體單元建立特定體積比的線棒-膠體板狀結構，在自由邊界條下對其進行模態分析，設其前5階的模態頻率（除去前6階自由模態）分別為F1、F2、F3、F4、F5。

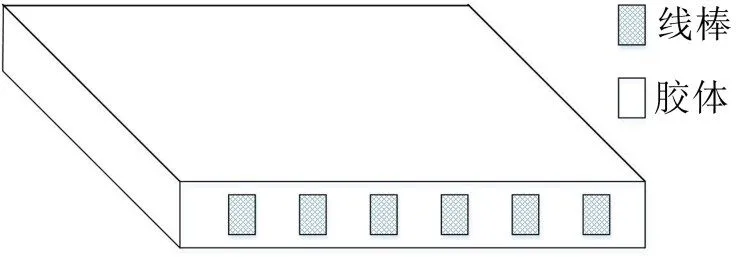
圖6板狀線棒膠體實體模型

采用實體單元另建立一塊相同形狀的均勻板狀結構，在自由邊界條件下對其進行模態分析，在保證其前5階模態振型（除去前6階自由模態）與線棒-膠體板狀結構相同的情況下，前5階模態頻率為f1、f2、f3、f4、f5。

等效均勻化方法是利用均勻化結構替代線棒-膠體結構，需要保證均勻化結構的動力學特性與實際結構相同。為此，建立如式(1)目標函數

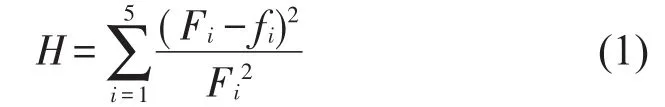
當目標函數H小于2.5×10-3時，每1階模態頻率的誤差均小于5%，以此保證線棒-膠體均勻化的等效材料參數足夠精確。具體材料參數利用ANSYS的優化功能來獲得。

（b）優化變量及優化結果

優化變量為：E1、E2、G12。基于經典復合材料理論給出優化變量的初值。設線棒走向為方向1，膠體厚度方向為方向3，另外一個方向為方向2，依據單層復合材料宏觀正交各向異性材料的材料參數表達式

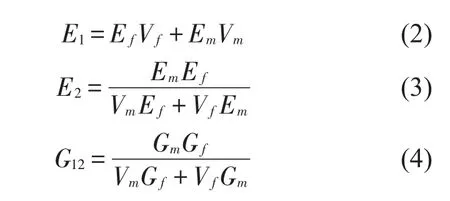
其中：Ef、G、μf、Vf分別表示線棒材料的彈性模量、剪切模量、泊松比以及線棒體積所占結構總體積的比重，Em、G、μm、Vm分別代表了膠體材料的對應特性參數。由式(2)、式(3)、式(4)獲得E1、E2、G12的初值，E3、G23、G13對模態頻率不產生影響[9]，以膠體材料的材料參數作為其初值。根據3個不同區域線棒和膠體的體積比，建立不同的線棒-膠體模型以及均勻化模型，通過ANSYS的1階優化方法進行迭代優化，獲得的材料參數如表3所示。數值計算表明，計算的結果不受結構形狀大小及模型的邊界條件影響。

4 模態分析及靈敏度分析

4.1 模態分析

至此，可建立定子端部的仿真模型。在自由狀態下對定子端部仿真模型進行模態分析，模態振型如圖7，模態頻率如表4所示。

采用錘擊法對端部結構進行模態實驗。測量時，在上層壓板表面布置兩圈測點，每一圈12個測點。錘擊法實驗得到的振型如圖8，模態頻率如表4所示。

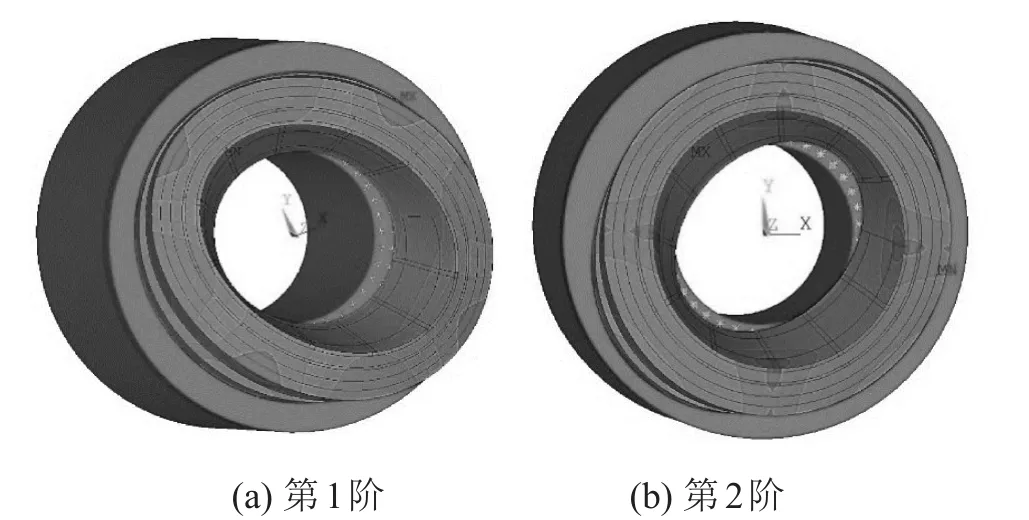
圖7 端部仿真模態振型

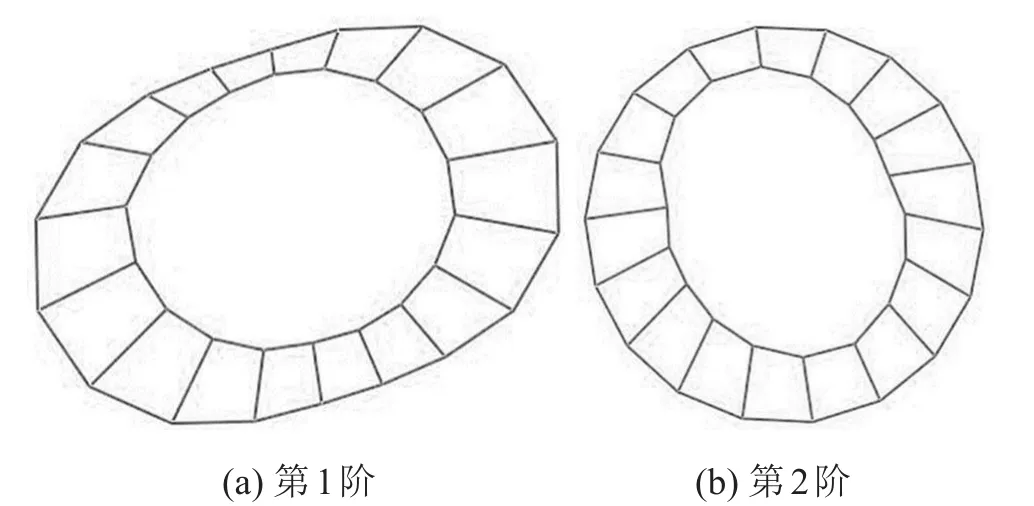
圖8 端部實驗模態振型

表3 線棒-膠體均勻化優化結果

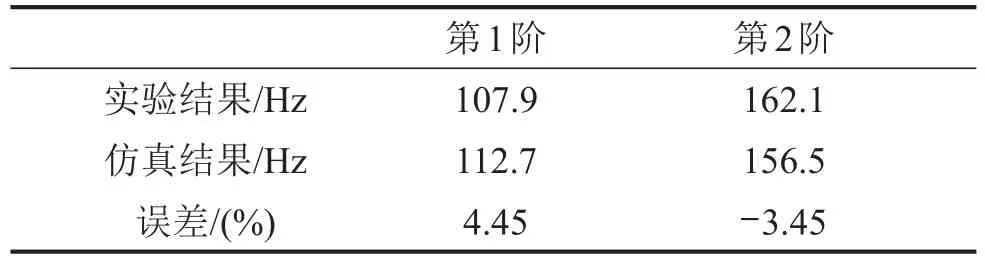
表4 端部模態實驗結果與仿真結果對比

如圖7所示，模態實驗得到定子端部的前2階振型均為橢圓振型，第1階振型靠鐵心一側振幅較小，另一側振幅較大，第2階振型靠鐵心一側振幅較大，另一側振幅較小，圖8仿真結果的模態振型與之相符。根據表5，仿真模型前兩階模態頻率的誤差均保持在5%以內。模態振型和模態頻率的對比結果表明，計算模型準確可靠。

4.2 靈敏度分析

為了對定子端部結構的動態設計提供指導意見，研究了端部1階模態頻率f對錐環上下沿的外徑D1、D2，上層壓板材料的彈性模量EX1和壓板厚度TH，層間壓板材料的彈性模量為EX2等參數的靈敏度。靠鐵心一側為錐環上沿，另一側為下沿。

通過ANSYS的1階優化方法，在第一次迭代之前獲得目標參數f對于這些變量的靈敏度，具體結果如表5所示。

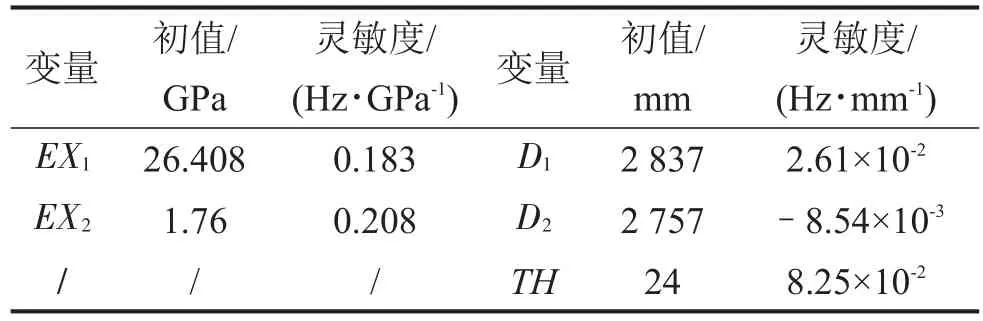
表51階端部模態頻率關于部分參數的靈敏度

根據上表結果，可以得到以下結論：

(1)假設材料參數的大小可以通過更換材料從而產生50%以內的改變，以此來分析材料參數對端部模態頻率產生的影響。EX1為上層壓板的彈性模量，而它的數量級在26 GPa左右，更換材料可以對端部1階模態頻率產生2 Hz左右的影響；EX2為層間壓板的彈性模量，由于其本身數量級太小，更換材料對定子端部1階模態頻率影響不到1 Hz，不予考慮。因此，可以通過更換上層壓板的材料來改變定子端部的1階模態頻率。

(2)D1為錐環上沿外徑，它的變化范圍為±300 mm，修改D1可以對端部模態產生8 Hz左右的影響，其余兩個參數的變化對端部1階模態頻率影響較小。因此，可以通過修改錐環上沿外徑D1來改變定子端部的1階模態頻率。

5 結語

通過接觸靜力學計算獲得錐環與定位支架的接觸剛度，用彈簧單元表征接觸剛度，實現了在定子端部模態分析中模觸邊界條件的模擬。提出了一種線棒-膠體的等效建模方式，將線棒-膠體等效成一種均勻的正交各向異性材料，降低其建模難度并提高精度。最后，通過計算靈敏度定量分析了端部各結構的材料參數和幾何參數對端部模態頻率的影響，發現上層壓板的彈性模量以及錐環的上沿外徑對端部的1階模態頻率影響較大，可以通過更換上層壓板的材料、修改錐環的上沿外徑來改變端部的1階模態頻率。

[1]白亞民.發電機定子繞組端部動態特性實驗的實踐意義和標準掌握[J].電力設備，2003(1)：56-59.

[2]黃偉，孫首群.大型汽輪發電機定子繞組端部模態仿真與實驗研究[J].噪聲與振動控制，2015，35(2)：41-43+136.

[3]趙清.大型汽輪發電機定子端部連接部位的處理及模態分析[J].上海電氣技術，2013，6(4)：20-23+40.

[4]楊昔科，吳新亞，李新巖，等.1000 MW級汽輪發電機定子端部繞組模態分析及有限元仿真[J].電機技術，2016，(06)：1-4.

[5]王益軒，朱繼梅.大型汽輪發電機定子端部繞組的動態仿真模型[J].機械工程學報，2005(9)：217-222.

[6]王益軒，朱繼梅.大型汽輪發電機定子端部繞組的動態優化設計[J].機械科學與技術，2008(2)：205-208.

[7]李輝光，劉恒，虞烈.考慮接觸剛度的燃氣輪機拉桿轉子動力特性研究[J].振動與沖擊，2012，31(7)：4-8.

[8]王玉田，袁曉紅.大型汽輪發電機定子繞組端部固定方法[J].大電機技術，2011(2)：15-16+19.

[9]陸韜，姜東，吳邵慶，等.2.5維C/SiC復合材料板彈性參數識別方法研究[J].振動與沖擊，2014，33(8)：42-47.