一種基于信度函數的復雜網絡重要節點識別方法

莫泓銘

(四川民族學院圖書館，四川康定 626001)

在科學技術突飛猛進的今天，人們的生活中充滿了各種各樣的信息化的系統，如電力系統、交通網絡系統、通信系統、在線社交系統等.這些應用系統或者本身就是網絡化的，或者可以抽象為網絡.復雜網絡的“無標度”[1]和“小世界”[2]等特性的發現，掀起了一輪又一輪的復雜網絡研究熱潮[3].在復雜網絡的眾多研究領域中，節點重要度識別一直是一個熱門話題.所謂重要節點，在不同的網絡結構或應用領域中有不同的理解.通俗地講，重要節點是相對的，它或它們相對于網絡中的其他非重要節點而言能更大程度地影響網絡的結構或功能[4].網絡中的重要節點的數量通常比較少，但通過它們，可以快速地影響到網絡中的絕大部分節點.比如，在無標度網絡中針對重要節點的蓄意攻擊可以快速導致網絡的級聯失效[5]，微博中的大V用戶所發布的信息可以快速傳遍微博[6]，等等.

尋找網絡中的重要節點，一方面可以通過其進一步挖掘網絡結構，另一方面可以對其加以重點利用，從而更好地優化網絡結構，促進網絡的良好運轉[7].研究者們提出了許多關于復雜網絡重要節點的識別方法，常見的有節點的度中心算法[8]、接近中心算法[9]、結構洞中心算法[10-11]等.這些算法大多是從節點單一屬性出發，或局部或全局地衡量節點的重要性.相關研究表明，節點是具有多重屬性的[12].如何利用節點的多屬性這一特性來更好更準確地識別復雜網絡中的重要節點是一個值得探討的問題.于會等[13-14]基于TOPSIS結合節點的度中心性、介數中心性、接近中心性和結構洞等屬性探討節點的重要度，常振超等[15]基于節點多屬性檢測網絡社團，李文蘭等[16]基于節點多屬性識別合著網絡中的關鍵節點.證據理論，又稱信度函數，作為一種不確定信息處理工具[17-18]，近年來被廣泛地運用于各類決策應用中[19-22].為了解決復雜網絡中的節點重要度識別問題，本文提出了一種基于信度函數的復雜網絡節點重要性識別方法，該方法將節點的度中心、接近中心性、結構洞等屬性視為不同的信度函數，運用證據理論中的組合規則將它們進行充分融合，得到節點的一個綜合評估值.實例驗證表明該方法具有有效性和全面性，能集成單一算法的優點同時克服其不足.

1 預備知識

1.1 常見的復雜網絡節點重要性算法

節點的度中心性(Degree Centrality)是指與節點直接相連的一級鄰居數量，其計算公式為：

(1)

其中，vij表示節點i與j直接相連的狀態，vij=1表示節點i與j之間有一條邊直接相連，vij=0表示節點i與j之間無直接邊相連.節點擁有的直接鄰居越多，其度越大，就越重要.節點度中心算法從網絡局部信息出發來衡量節點的重要性，具有簡單、快捷等特點.然而，網絡中的許多節點通常具有相同數量的一級鄰居，其度值相同，在這種情況下，度中心算法視它們的重要程序一樣，因而無法進一步區分.

節點的接近中心性(Closeness Centrality)衡量的是從某個特定節點出發到網絡中其他節點的最短路徑所含邊的數量的倒數，其計算公式為：

(2)

其中，dij代表節點i與節點j之間的最短路徑中的邊的數量.

接近中心算法是節點在網絡中所處的位置這一屬性出發來衡量節點的重要性.節點的接近中心值越大，說明其在網絡中處于中心位置的可能越大，就越重要.節點的接近中心算法從網絡全局的角度來衡量節點的重要程序，需遍歷整個網絡，相對度中心算法而言，其運算復雜度較高.

1.2 結構洞

結構洞理論是由美國社會學家Burt在其著作《結構洞：競爭的社會結構》中提出的[9].Burt認為網絡中的位置比關系的強弱更為重要，節點在網絡中的位置決定了其地位的高低，相應地擁有更多的信息、資源與權力.結構洞理論認為，如果兩個節點之間無法直接聯系，必須通過第三者才能取得聯系，那么這兩個節點之間的第三者就占據了一個結構洞.衡量結構洞的指標有網絡約束系數(Constraint，CT)、網絡有效規模(Effective Size，ES)、效率(Efficient，EF)、等級度(Hierarchy，HI)等，不同的指標適用于不同的應用場合.在本文中，采用網絡約束系數作為衡量結構洞的指標.網絡約束系數是指網絡節點形成結構洞時所受到的約束，其計算公式為：

(3)

其中，Γ(i)為節點i的所有一級鄰居的集合，節點q為節點i與j的共同鄰居.pij為節點i為維持與節點j的鄰居關系所付出的精力與總精力的比例，piq和pqj分別為節點i與j與共同鄰居q維持關系所付出精力占其總精力的比例.pij的計算公式如下：

(4)

其中，zij表示節點i到j的關系，當節點i到j之間有聯系時，其值為1，否則為0.piq和pqj的計算公式與pij類似.

結合公式(3)和(4)可知，節點的網絡約束系數指標能夠反映節點的一級鄰居數量及它們之間聯系的緊密程度情況.節點i的度越大，則其一級鄰居數量越多，pij的值就越小，說明一級鄰居數量越多的節點更容易形成結構洞.piq和pqj從節點的共同鄰居的角度出發，節點i,j,q之間聯系越緊密，它們之間形成的三角形拓撲結構就越多.由此可見，節點的網絡約束系數值就越大，說明該節點的鄰居很少且與其他鄰居的閉合或重合程度很高，這類節點的影響范圍有限，不易獲得更多的新的關系支援，因而在競爭中處于不利的地位.反之，節點的網絡約束系數越小，其越容易形成結構洞，進而有利于獲得新的關系支援，在競爭中處于有利的地位，即網絡約束系數小的節點在網絡中的影響力較大.結構洞理論在復雜網絡的節點重要度識別[23-26]、社會網絡分析[27-28]和企業管理[29]等方面得到了廣泛應用.

1.3 信度函數

信度函數理論又稱為證據理論，是Dempster于1967年提出的[17]，其試圖運用傳統概率中的上下限來表達實際問題中的不確定性，隨后其學生Shafer于1976年對其進行了進一步推廣[18].證據理論相比較傳統的主觀貝葉斯理論，最大的特點在于不需要先驗信息，并且可以直接表達“不確定”與“不知道”.證據理論中的信度函數允許我們基于信度和組合規則，使用一個問題的概率來推導另一個相關問題的概率.證據理論的相關概念簡要介紹如下：

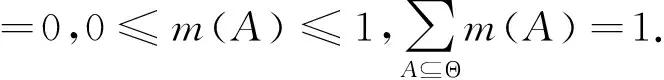
(5)

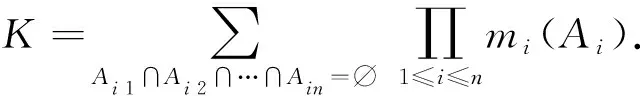
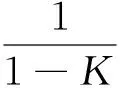
2 基于信度函數的融合節點重要度識別模型

基于信度函數的節點重要度識別模型如圖1所示，主要由以下幾部分構成：①選擇節點相關屬性；②測定相關選定屬性值；③構建信度函數框架并將測得的屬性值轉換為信度函數；④運用Dempster組合規則融合節點屬性信度函數；⑤分析融合結果并據此排序.

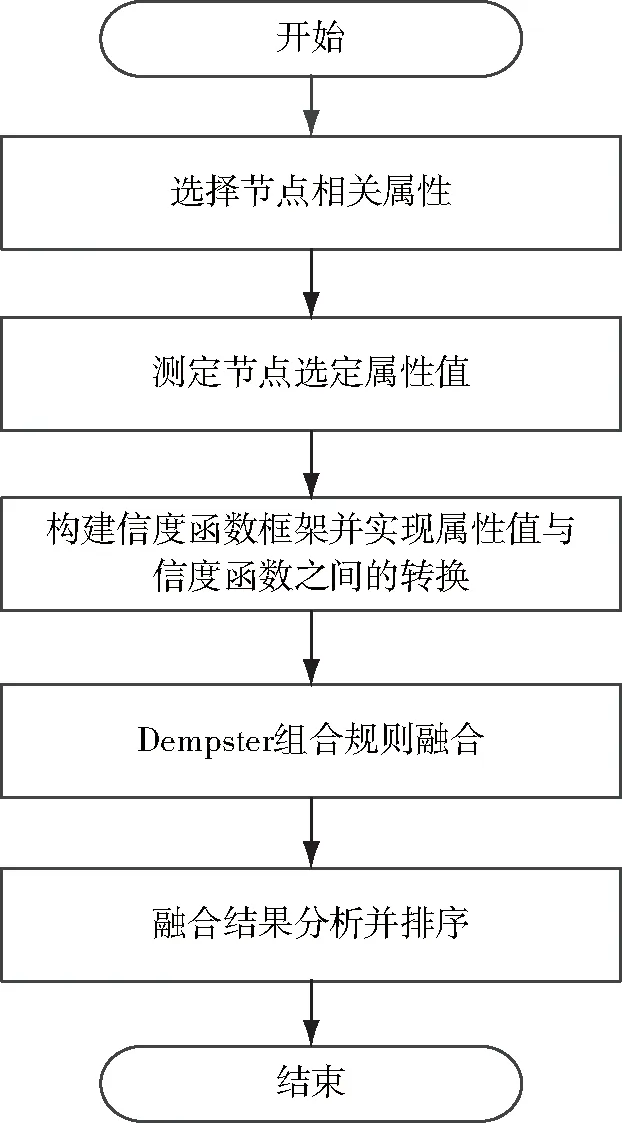
圖1 基于信度函數的復雜網絡節點重要度識別模型

3 實例應用

在本例中，采用USAir97數據集來驗證本模型的有效性.USAir97是一個加權的有向網絡，為簡便描述，將其視為無權的無向網絡.USAir97數據集中包含了332個節點、2126條邊，節點的最大度值為139，最小為1[30].USAir97網絡如圖2所示.下面將運用新建立的節點重要度識別模型來識別USAir97網絡中節點的重要度情況.

圖2 USAir97網絡

Step1 結合USAir97網絡特性，選取節點的度、緊密度和結構洞等屬性作為測定指標.

Step2 分別運用相關算法，測得節點的度、緊密度和結構洞等屬性值，如表1中第2、4、6列所示.需要說明的是，由于結構洞屬性中的網絡約束系數是一個逆指標，即數值越小其影響力越大，而度與緊密度指標均是正向指標，為統一測量指標體系，需對節點的網絡約束系數值進行相應處理.由于該網絡節點眾多，限于篇幅，表1只列出了部分節點.

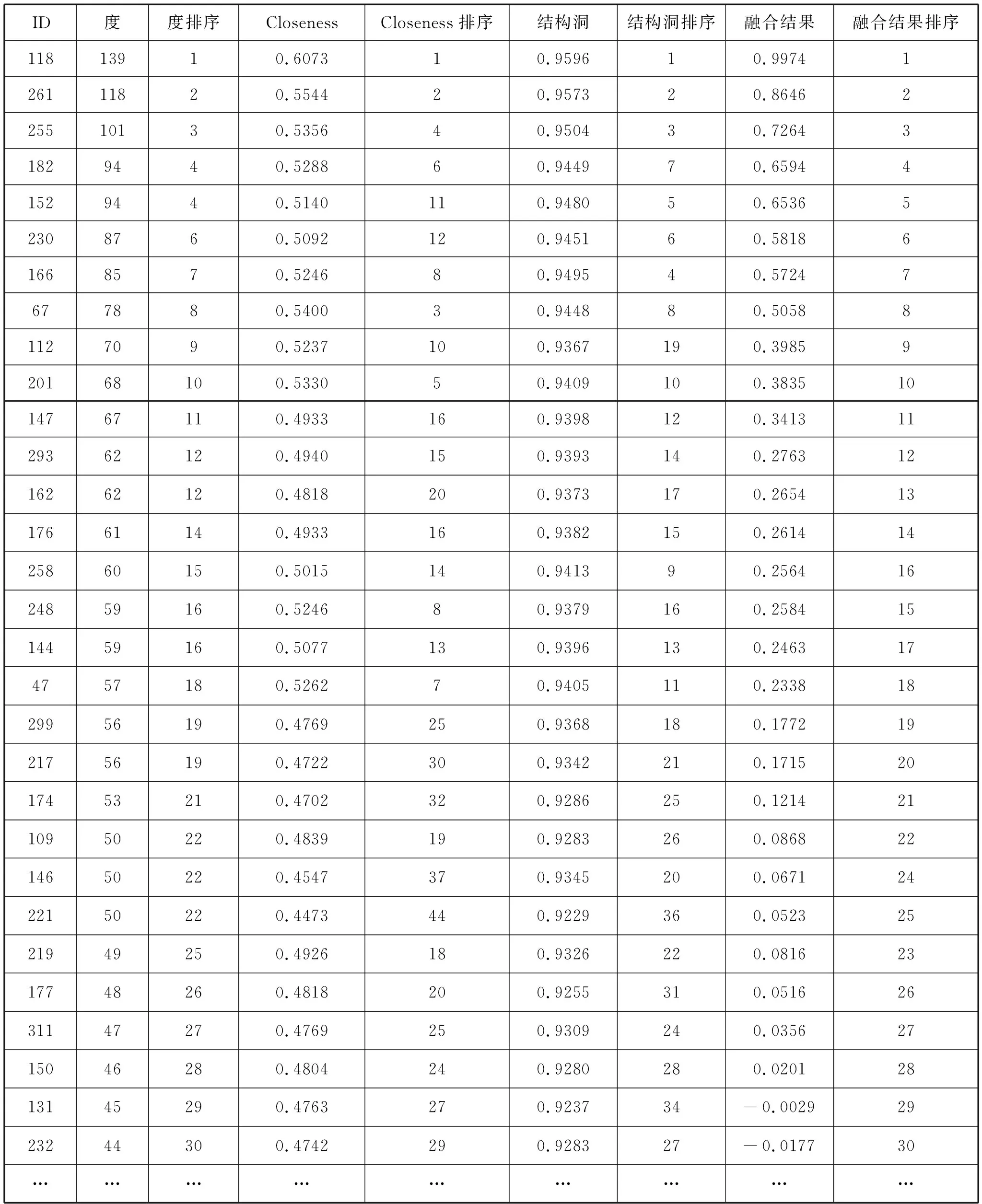
表1 節點相關屬性值及排序

Step3 構建信度函數理論框架.在本例中，主要測試節點的重要程度，即可簡單地將節點的重要與否劃分為重要與不重要，即其辨識框架為{重要，不重要}，數學化表示為Θ={H,L}.Θ為辨識框架，H代表重要，L代表不重要.建立好辨識框架后，接下來需要將相關屬性值轉化為信度函數的形式.

首先，選擇參考值.選擇相關屬性值的最大值和最小值作為參考值，則：

DCmax=max{DC1,DC2,DC3,…,DCn},

DCmin=min{DC1,DC2,DC3,…,DCn},

CCmax=max{CC1,CC2,CC3,…,CCn},

CCmin=min{CC1,CC2,CC3,…,CCn},

Cmax=max{C1,C2,C3,…,Cn},

Cmin=min{C1,C2,C3,…,Cn}.

其中，DCmax為度值中的最大值，DCmin為度值中的最小值，CCmax為聚集系數值中的最大值，CCmin為聚集系數值中的最小值，Cmax為結構洞屬性中網絡約束系數值中的最大值，Cmin為結構洞屬性中網絡約束系數值中的最小值，即DCmax=139,DCmin=1,CCmax=0.6073,CCmin=0.1978,Cmax=0.9596,Cmin=0.

其次，構建信度函數轉換模型.以節點i的度為例，mDCi(H)和mDCi(L)分別代表節點i在度中心算法中的重要程度與不重要程度，同理有mCCi(H)、mCCi(L)、mCi(H)和mCi(L).節點i的相關屬性的信度函數可通過下列模型轉換得到：

其中，ω為可調節參數，其目的在于避免當最大值與最小值一樣時上述轉換模型出現分母為0的情況.理論上，ω可取值為任意非零實數，為簡便，在本模型中ω取值為1.節點i的各相關屬性信度函數經整理，有：

MDC(i)=(mDCi(H),mDCi(L),mDCi(Θ)),

MCC(i)=(mCCi(H),mCCi(L),mCCi(Θ)),

MC(i)=(mCi(H),mCi(L),mCi(Θ)).

其中，

mDCi(Θ)=1-mDCi(H)-mDCi(L),

mCCi(Θ)=1-mCCi(H)-mCCi(L),

mCi(Θ)=1-mCi(H)-mCi(L).

以節點118為例，節點118的度、聚集系數、結構洞為：

整理可得節點1的各屬性信度函數有：

MDC(118)=(mDC118(H),mDC118(L),mDC118(Θ))=(0.9928,0,0.0072).

(6)

MCC(118)=(mCC118(H),mCC118(L),mCC118(Θ))=(0.2905,0,0.7095).

(7)

MC(118)=(mC118(H),mC118(L),mC118(Θ))=(0.4897,0,0.5103).

(8)

Step4 融合相關信度函數.在得到節點各屬性的信度函數后，運用Dempster組合規則，對節點屬性的信度函數進行兩兩融合，最終得到節點的一個綜合決策信度函數：

M(i)=(mi(H),mi(L),mi(Θ)).

(9)

在本例中，對節點1，運用公式(5)，依次融合公式(6)～(8)，得到節點118的綜合決策信度函數：

M(118)=(m118(H),m118(L),m118(Θ))=(0.9974,0,0.0026).

(10)

Step5 公式(9)中的mi(Θ)代表系統無法進一步將該部分數值分配給H或L，在本模型中，為簡便起見，將mi(Θ)平均分配給mi(H)和mi(L).則節點的融合最終值可由如下公式獲得：

(11)

對節點1，有F(118)=m118(H)-m118(L)=0.9947-0=0.9947.

重復上述步驟，同理可得其它節點的融合最終值，如表1中第8列所示.

4 分析討論

由表1中第2～3列可看出，度中心算法從節點的鄰居數量這一局部屬性出發，能快速地計算出網絡中各節點的一級鄰居數量，并依此進行排序，然而對于度值相同的節點，其無法進一步區分其重要性，只能將它們視作同等重要，如節點182和節點152，節點293和節點162等.緊密度中心從節點在網絡中所處的位置這一全局屬性出發來衡量節點的影響力，表1的第4～5列表明，那些處于網絡拓樸中心地位的節點更為重要，能識別不同網絡的不同影響力，特別是對于那些度值相同的節點，能根據它們的位置信息進行有效的區分，如節點182和節點152雖然都具有相同的鄰居數，但由于它們在網絡中所處的位置不同，因而其排名也不同，分別為6和11.結構洞算法從當前節點的鄰居的角度來考量節點的影響力，其不僅考量節點的一級鄰居數量，還將節點的鄰居對該節點的貢獻及鄰居的影響力等納入了考慮范圍.表1中的第6～7列表明，節點所擁有的鄰居數量及鄰居的影響力也是很重要的，如節點182和節點152，雖然都擁有相同數量的一級鄰居，但由于鄰居的影響力不一樣，因而它們的排序也不一樣.總體而言，上述三種方法都是從特定角度來衡量節點的影響力，有側重，也有不足，得到的結果也有差異.網絡中的節點不是孤立存在的，它受網絡拓樸、節點鄰居數量、鄰居的影響力等多方因素的影響.節點是多屬性的.在本文中，基于信度函數通過融合節點的多種屬性，以期更為準確地衡量節點的影響力.從表1中的第8～9列可以看出，新方法通過融合節點的度、緊密度和結構洞等屬性，最終得到節點的綜合唯一評估值，且不存在無法進一步區分的情況.從排序結果來看，本文方法較好地考慮了節點的度中心、緊密度中心和結構洞中心等因素，排名前10的節點分別覆蓋了度中心、緊密度中心和結構洞中心的前10、9和7個節點.

5 結語

本文提出了一種基于信度函數的復雜網絡中識別節點重要性的方法，通過將節點的相關屬性轉換為信度函數并據此進行融合，最終得到節點的綜合評價指標值并以此排序.實例驗證表明，此方法是有效的，能夠綜合節點單一屬性算法的優點，并克服單一屬性算法的不足.需要說明的是，本文提出的方法僅考慮了節點的少數屬性，并且僅運用于無向無權的網絡中，在下一步的工作中，我們將考慮融合節點更多的屬性，并且將該方法進一步推廣運用到有向有權的網絡中.

[參考文獻]

[1]Albert-László Barabási,Réka Albert.Emergence of scaling in random networks[J].Science,1999(286):509-512.

[2]Duncan J Watts,Steven H Strogatz.Collective dynamics of‘small-world’networks[J].Nature,1998(393): 440-442.

[3]周濤,張子柯,陳關榮,等.復雜網絡研究的機遇與挑戰[J].電子科技大學學報,2014(1):1-5.

[4]任曉龍,呂琳媛.網絡重要節點排序方法綜述[J].科學通報,2014(13):1175-1197.

[5]Réka Albert,Hawoong Jeong,Albert-László Barabási.Error and attack tolerance of complex networks[J].Nature, 2000(406):378-382.

[6]Jianshu Weng,Ee-Peng Lim,Jing Jiang,et al.Twitterrank:finding topic-sensitive influential twitterers[C]. ACM,2010:261-270.

[7]莫泓銘.節點重要度在復雜網絡魯棒性中的應用[J].長春師范大學學報,2016(2):22-25.

[8]Linton C Freeman.Centrality in social networks conceptual clarification[J].Social networks,1978(3):215-239.

[9]Kazuya Okamoto,Wei Chen,Xiang-Yang Li.Ranking of closeness centrality for large-scale social networks[J]. Lecture Notes in Computer Science,2008(59):186-195.

[10]Phillip Bonacich.Factoring and weighting approaches to status scores and clique identification[J].Journal of Mathematical Sociology,1972(1):113-120.

[11]張惠玲,張蒙.基于結構洞指數的網絡節點重要度評估[J].計算技術與自動化,2016(1):101-103.

[12]王勁松,李宗育,徐晏琦.基于多屬性決策的復雜網絡節點攻擊研究[J].電光與控制,2016(4):42-47.

[13]Ronald S Burt.Structural holes:the social structure of competition[M].Harvard University Press,2009.

[14]于會,劉尊,李勇軍.基于多屬性決策的復雜網絡節點重要性綜合評價方法[J].物理學報,2013(2):46-54.

[15]常振超,陳鴻昶,劉陽,等.基于聯合矩陣分解的節點多屬性網絡社團檢測[J].物理學報,2015(21):456-465.

[16]李文蘭,王野,李立,等.基于多屬性決策合著網絡關鍵節點識別研究[J].情報理論與實踐,2017(9):95-100.

[17]Arthur P Dempster.Upper and lower probabilities induced by a multivalued mapping[J].The Annals of Mathematical Statistics,1967(2):325-339.

[18]Glenn Shafer.A mathematical theory of evidence[M].Princeton University Press,1976.

[19]蔣雯,張安,鄧勇.基于信度函數的決策及應用[J].計算機工程與應用,2008(31):36-38.

[20]莫泓銘,夏齡.基于證據理論的川西水電開發生態環境評價研究[J].長春師范大學學報,2017(2):35-40.

[21]趙汝鵬,田潤瀾,王曉峰.基于證據理論的雷達信號融合識別算法改進研究[J].電子技術應用,2017(6):19-22.

[22]韓德強,楊藝,韓崇昭.DS證據理論研究進展及相關問題探討[J].控制與決策,2014(1):1-11.

[23]王運明,王青野,潘成勝,等.面向結構洞的指揮控制網絡關鍵節點識別方法[J].火力與指揮控制,2017(3):59-63.

[24]劉世超,朱福喜,馮曦.復雜網絡的重疊社區及社區間的結構洞識別[J].電子學報,2016(11):2600-2606.

[25]韓忠明,吳楊,譚旭升,等.面向結構洞的復雜網絡關鍵節點排序[J].物理學報,2015(5):421-429.

[26]蘇曉萍,宋玉蓉.利用鄰域“結構洞”尋找社會網絡中最具影響力節點[J].物理學報,2015(2):1-11.

[27]廖麗平,胡仁杰,張光宇.模糊社會網絡的結構洞分析方法[J].東南大學學報:自然科學版,2013(4):900-904.

[28]郭秋萍,趙靜,郭祥.基于結構洞的人際情報網絡分析[J].情報理論與實踐,2016(3):26-31.

[29]章丹,胡祖光.網絡結構洞對企業技術創新活動的影響研究[J].科研管理,2013(6):34-41.

[30]V Batageli,Mrvar A.Pajek datasets[EB/OL].(2013-11-07)[2017-02-15].http://vlado.fmf.uni-lj.si/pub/networks/data/default.htm.