基于分布式計算的大數據聚類算法預測強度優化研究

郭燁旻

(吉林工程技術師范學院信息工程學院，吉林長春 130052)

大數據聚類算法的應用主要集中在圖形處理、模式匹配、市場分析等領域。大數據的聚類分析研究存在著各種困難，而這些困難是由大數據本身的特點所決定的。進入大數據時代后需要處理的數據量規模劇增，使用串行方式進行數據分析的傳統聚類方法已經難以適應當前云計算網絡環境下的數據處理需求，本研究采用并行的方式，以預測強度為切入點對大數據聚類算法進行研究和優化。

對某一指定的數據集以其一項或幾項屬性為出發點，對其進行分類的這一過程被稱為聚類，而在聚類的過程中并不需要對數據集的全部屬性進行充分的了解。一般將所分的多個類別中的每一個稱為一個蔟(Cluster)，以數據在一項或幾項特定屬性上的相似度，作為不同蔟之間的劃分標準。所以，在聚類的過程中并不需要預先設置分類標準，而是以數據本身的特定屬性為依據，自動進行分類。

1 數據分析系統

當前大數據分析處理系統主要有兩大方向：以Hadoop為代表的批處理系統；為特定應用所開發的流處理(Stream Processing)系統。其主要區別在于批處理系統需要儲存后再處理，而流處理系統則是直接處理。單一的數據分析處理系統對當前云計算網絡環境下數據量劇增的情況難以適應，應用體系結構與底層設計語言混合以及大數據處理高層計算模式混合的混合式數據分析系統更加適應當前的應用需要。

2 預測強度優化的聚類算法

預期中要將數據集劃分為蔟的數量是聚類過程中的重要參數，本研究在計算聚類數時使用Tibshirani在2001年提出的基于預測強度的方法。

具體的計算步驟為：

(1)將當前數據集以隨機劃分的方式分為測試集A和測試集B；

(2)以k作為當前聚類數，對兩個子集進行聚類，記錄結果；

(3)將兩個子集的聚類結果進行判別；

(4)統計集合A所有蔟中的樣本在集合B中的分類誤差，計算分配的正確率；

(5)以k為聚類數的預測強度為所有正確率中的最小值。

在預測強度定義中，C(A,k)表示將集合A聚為k類，Akj表示集合B聚成的第j類，nkj代表Akj中的元素數量，D[C(A,k),B]ii′為聚類結果判別矩陣中i行i′列的元素值。由此可見，預測強度值pk(s)∈[0,1]，受聚類數影響。預測強度值越大，說明當前聚類算法能夠將新數據元素劃分到正確的蔟的預測能力越強。

預測集合和測試集合對數據的隨機劃分，會導致預測強度受到偶然因素干擾比較嚴重。本文提出將數據先行劃分成多個隨機類，分別作為測試集計算預測強度，取多個預測強度的平均值作為當前聚類數下的最終預測強度，從而減小偶然因素對預測強度的干擾，起到優化算法的作用。

通過預測強度確定聚類數k，從而進行聚類的對應算法如下：

輸入：數據集D={d1,d2,…,di,…,dn}，當前最佳聚類數k

(1)從D集合中選取k個屬于D的數據點d1′,…,dk′作為聚類后的蔟的質心；

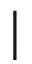
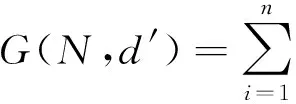
(5)循環運行步驟(2)和步驟(3)，直到(4)的值不再變化，顯而易見，準則函數值是在不斷縮小的。

其中，Nj應為距數據di最近的質心dj′所在的蔟，sign(Nj=j)表示當Nj=j時其值為1，其他所有情況其值為0。

輸出：質心d1′,…,dk′所在的蔟N1,…,Nk

取某直播平臺訪客在不同欄目上停留時間的數據，輸入三個欄目的數據，以主播數量3作為變量數進行分析。選用BIC準則建立模型，生成變量數與聚類數之間的函數曲線，對比優化后的基于預測強度的變量數與聚類數關系函數曲線如圖1所示。

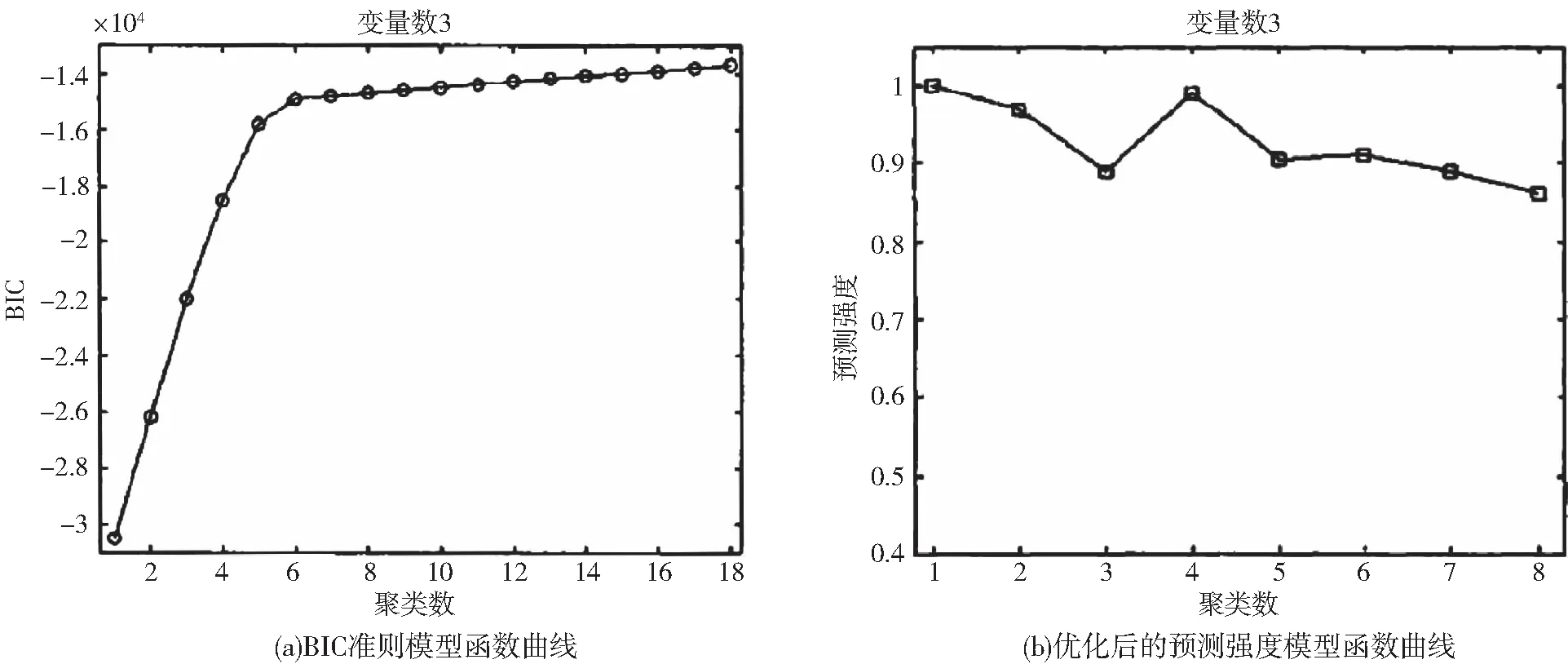
圖1 優化后算法與已有算法對比圖

在相同變量數的條件下，BIC準則本身對聚類數的確定沒有影響，從使用BIC準則的圖1中可看出，當聚類數超過4之后圖像趨于平穩，受偶然因素干擾程度較小，聚類數應為超過4的值，但無法完全確定具體取值。而使用優化后的算法可得到聚類數為4時預測強度有最大值，能夠較為準確地確定聚類數。

按照測試強度確定聚類數為4，聚類分析后的曲線如圖2所示。

通過對圖2的分析可以明顯看出，具有第一類屬性的訪客對大部分欄目都有較大的興趣，他們所具有的屬性與平臺的欄目設置方向一致性較大，對該屬性用戶的服務可以做適當的傾斜。而第四類用戶明顯對平臺當前的內容興趣欠缺，在沒有開設新欄目之前可以對具有第四類屬性的用戶適當忽略。

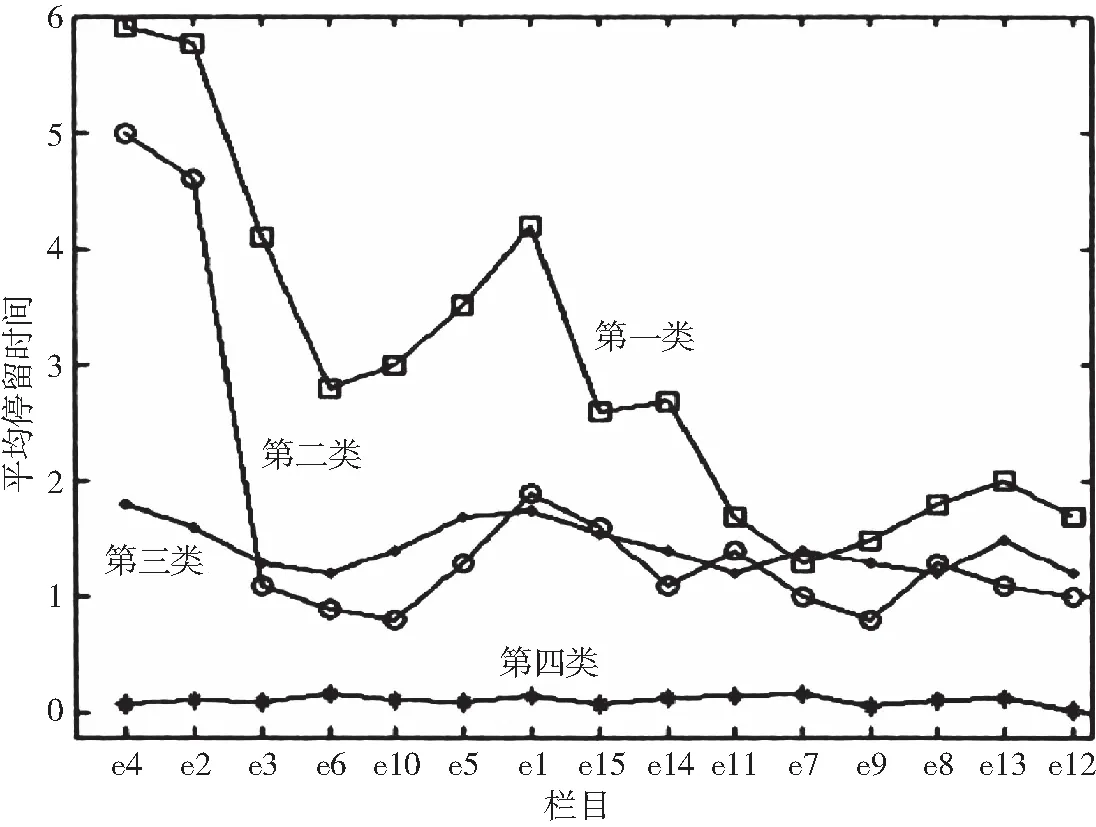
圖2 不同類訪客在所有欄目上的平均停留時間

3 結語

通過以上測試可以看到優化后的聚類算法在實際應用中的作用。以傳統聚類算法為基礎，對確定具體聚類數量的方法進行適當的優化，可以有效地減少偶然因素對聚類結果的干擾，使用該算法在進行大量數據聚類分析時能夠有效地減少時間復雜度以及經濟支出，具有一定的應用價值。

[參考文獻]

[1]李國杰,程學旗.大數據研究:未來科技及經濟社會發展的重大戰略領域——大數據的研究現狀與科學思考[J].網絡新媒體技術,2012(6):647-657.

[2]黃宜華.深入理解大數據:大數據處理與編程實踐[M].北京:機械工業出版社,2014.

[3]楊彥侃.并行的聚類算法研究[D].包頭:內蒙古科技大學,2010.

[4]R Tibshirani,G Walther.Cluster Validation by Predication Strength[J].Journal of Computational & Graphical Statistics,2005(3):511-528.