離散社會群體優(yōu)化算法求解旅行商問題
劉亞軍,陳得寶,鄒 鋒,王蘇霞,吳樂會
(淮北師范大學物理與電子信息學院,安徽淮北 235000)
[通訊作者]陳得寶(1975- ),男,教授,碩士生導師,博士,從事智能計算、模式識別研究。
社會群體優(yōu)化算法(SGO)是Suresh Satapathy等于2016年提出的一種新型優(yōu)化算法[1],源自社會群體學習知識提高能力的過程。此算法操作簡單,易于實現(xiàn),故在一些問題優(yōu)化中取得了良好的效果[2]。與其他算法相比,SGO算法在兩個學習階段都以群體最好的個體作為學習向導,算法的收斂速度較快。因此,在優(yōu)化領域,SGO算法在連續(xù)域問題求解上取得了不錯的效果。SGO算法作為一種新型優(yōu)化算法,在離散域問題上的應用較少。為了使SGO算法在離散問題的解決中也取得不錯的效果,本文研究離散后的SGO算法在TSP中的應用,并分析了仿真后的結果。
本文主要對SGO算法進行離散化處理,并用于求解TSP問題。首先介紹TSP問題模型和基本SGO算法,接著將基本SGO算法的運算規(guī)則進行離散化處理,最后通過TSP問題的仿真實驗。結果表明,社會群體優(yōu)化算法在解決TSP問題中具有良好的性能。
1 TSP模型和基本SGO算法
1.1 TSP問題模型
旅行商問題(Traveling Salesman Problem,TSP)是一個典型的NP完全問題[3]。TSP問題目的:從某一個城市出發(fā),找到一條通過所有城市再回到起點的最短路徑,每座城市必須且只能訪問一次。TSP已經被證明是NP完全問題,且在車輛調度、物流管理等方面具有廣泛的應用[4]。研究人員對此提出多種優(yōu)化算法來解決TSP問題,都取得了不錯的效果。如遺傳算法(GA)[5]、粒子群優(yōu)化算法(PSO)[6]、蟻群算法(ACO)[7]等。本文采用TSPLIB中的TSP數據作為此次實驗數據及優(yōu)化結果的對比數據。
1.2 基本SGO算法
SGO算法是一種基于社會群體學習和提升自身解決問題能力的新型優(yōu)化算法。在現(xiàn)實生活中,很多工作或者難題的處理需要多方面因素的參與。當學習者欠缺此方面的能力時,須向周圍或擁有此項能力的個體學習,以便達到相應的目的。SGO算法是基于此種思想提出的,其實現(xiàn)過程主要包含三個步驟:種群初始化、提高階段學習、獲得階段學習。
1.2.1 種群初始化
隨機初始化種群P,如式(1)所示。
Xi,j=xmin+r*(1,D)*(xmax-xmin).
(1)
其中,i=1,2,…,N,j=1,2,…,D,N為種群的規(guī)模,D為變量的維數;r∈[0,1];xmax與xmin分別為變量的上限與下限;P為進化種群,X為個體位置。
1.2.2 提高階段學習
SGO算法在此階段采用的學習策略如式(2)所示。
Xnewi,j=c*Xoldi,j+r*(gbestj-Xoldi,j).
(2)
其中,c為自我反省參數,c∈[0,1]。文獻[1]實驗結果表明,當c為0.2時,算法效果較好;gbestj為當前最優(yōu)個體的第j維變量。Xnewi,j與Xoldi,j分別為第i個個體更新前后的第j維變量。
1.2.3 獲得階段學習
在獲得階段,每個個體從種群中隨機選擇一個個體作為學習對象,并結合當前代群體的最優(yōu)個體信息進行學習,具體學習方法如式(3)(4)所示。
Iff(Xi)isbetterthanf(Xk):
Xnewi,j=Xoldi,j+r1*(Xi,j-Xk,j)+r2*(gbestj-Xi,j).
(3)
Else
Xnewi,j=Xoldi,j+r1*(Xk,j-Xi,j)+r2*(gbestj-Xi,j).
(4)
其中,Xi,j與Xk,j分別為個體i和個體k的第j維變量;Xnewi,j與Xoldi,j分別為第i個個體更新前后的第j維變量;gbestj為當前代最優(yōu)個體的第j維變量。
2 離散SGO算法
SGO算法最初是用來優(yōu)化連續(xù)域函數問題的,而在實際工程應用中有很多組合優(yōu)化問題屬于離散域范疇。基于這個前提,本文在基本SGO算法的基礎上發(fā)展了離散SGO算法來求解離散化問題。離散化問題的典型代表是TSP問題,本文以提出的離散SGO算法來解決TSP問題,提出的離散SGO算法易于實現(xiàn)。操作步驟:首先,使用隨機初始化策略產生一個具有NP個學習者的種群;其次,獲取此種群中的最優(yōu)個體作為教師;然后,在提高階段和獲得階段分別采用交叉、變異操作來生成新學習者,以此提高種群的多樣性;最后,通過對原學習者和新學習者的比較進行種群更新。
2.1 個體初始化和教師的確定
在此階段TSP問題中,采用隨機初始化方法生成學習者群體。假設群體的大小為NP,求解的TSP問題的城市規(guī)模為N,則初始化后會生成一個NP×N的矩陣。矩陣中的第i行對應著第i個學習者個體,學習者個體的每一列代表一個城市,從第1列到第N列代表著對應城市遍訪順序。第i個學習者個體的初始化公式如下:
Xi=randperm(N).
(5)
其中,randperm(N)表示產生一個包含數值1到N的隨機排列的N維向量。
在基本SGO算法中,種群中個體向當代本群的最好個體(即教師)學習知識,提高自身的能力,學習者的更新是根據教師來實現(xiàn)的。Teacher為種群中的最好學習者個體,其表達式如下所示:
Teacher=Best(X1,X2,…,Xi).
(6)
其中,X1,X2,…,Xi為種群中學習者個體。
2.2 離散SGO算法的提高階段
在基本SGO算法的提高階段,學習者是根據式(2)更新知識的,但這適用于優(yōu)化連續(xù)域問題,而TSP問題屬于離散化范疇。因此,應重新定義學習者的更新方法來求解TSP問題。在提高階段的更新公式如下所示:
TXi=Xi?Teacher.
(7)
其中,?表示交叉操作。
交叉操作的具體步驟可以概述如下:
假設以種群中任意兩個學習者個體A和B為例:
然后,隨機從A、B中選擇兩段基因位,并交換兩段基因位中相對應的元素,得到:
由于在AA、BB中出現(xiàn)了遍歷重復,根據位置合法性檢測,逐一交換,得到newA、newB:
以上交叉操作完成后,接著執(zhí)行變異操作來產生新的學習者,更新公式如下:
newXi=ΘTXi.
(8)
其中,Θ表示變異操作。
在本文中,種群中采用的是翻轉變異,其具體操作步驟如下:在城市序列中隨機選擇兩基因位,再將這兩基因位內的子序列按反序插入原位置。如序列newA的兩基因位為2和6,則經翻轉后,得到新學習者newAA如下:
與基本SGO算法一樣,在提高階段這兩部分操作完成后,種群會產生新的學習者,新的學習者的學習能力可能比原先的學習者的能力強。若是這樣,種群中學習能力強的學習者將會取代能力差的個體,其更新可以描述為:如果f(newXi) 在基本SGO算法的獲得階段,種群中學習者Xi是根據當前從種群中隨機選擇的學習者Xj之間的差異及當前種群最好學習者的信息進行知識更新的。在離散SGO算法中,此操作可以被定義如下: TXi=Xi?Xj. (9) TXi=Xi?Teacher. (10) 其中,?表示交叉操作,與提高階段的交叉操作一樣;Teacher=Best(X1,X2,…,Xi)。 同提高階段一樣,當交叉操作完成后,接著進行變異操作來產生新的學習者。獲得階段的變異采用的也是翻轉變異,其操作流程與提高階段相同,表達式如下: newXi=ΘTXi. (11) 其中,Θ表示變異操作。 與基本SGO算法一樣,在獲得階段這兩部分操作完成后,種群會產生新的學習者。學習能力強的學習者將會取代能力差的個體,其更新可以描述如下:如果f(newXi) 為了驗證離散SGO算法的有效性與正確性,選用6個TSP標準測試問題進行實驗仿真測試,并與其他4個算法進行比較,得出相應的結果。 為了檢驗算法的有效性,選取在TSPLIB庫中不同城市樣例。選取的比較算法在合適的參數下方能達到較為理想的結果。本文選取的4個比較算法是分別是ACO[8]、ABC[9]、GA和PSO算法。GA、PSO與SGO算法的參數設置如下: SGO:pc=2,pm=0.1; GA:pc=0.8,pm=0.4; PSO:pm=0.3,個體經驗保留概率為0.25,全局經驗保留概率為0.55。 本文所有算法的種群規(guī)模均設置成40,迭代次數設置為1000。為了測試結果的真實性,每個算法獨立運行20次。 各算法仿真結果如表1所示。KOS表示在TSPLIB中已知的最好解,加粗的數字表示各個算法對不同城市個數的TSP問題獨立運行20次時所得到的平均最優(yōu)結果。 表1 試驗結果的比較 從表1可以看出,對于burma14問題,PSO、GA與SGO算法在獨立運行20次后的平均值均能達到已知最優(yōu)解30.87;對于Oliver30問題,ACO、SGO的最優(yōu)解均是423.74,比已知最優(yōu)解相差0.24,相比較其他3種算法效果要好;對于chn31問題,SGO算法的最優(yōu)結果達到了已知最優(yōu)結果15381,而其他4種算法最優(yōu)解均不能達到已知最優(yōu)解15381;對于dantzig42問題,SGO算法最優(yōu)解692.03,要比已知最優(yōu)解699好,ABC算法同樣達到了已知最優(yōu)解;對于st70和kroA100問題,SGO算法雖都未能達到已知最優(yōu)解,但是較其他3種算法結果要好,更接近已知最優(yōu)解。從表1中數據可以看出,SGO算法在求解TSP問題上有明顯的優(yōu)勢。 為了證明SGO算法的有效性,本文以chn31為例進行簡單證明。圖1為SGO算法在chn31下最優(yōu)路徑回路圖,圖2為SGO算法在chn31下的迭代收斂曲線圖。對于SGO算法,隨著迭代的進行,算法收斂速度較快(僅迭代了180代左右就實現(xiàn)了最優(yōu)),從而搜索路徑更優(yōu)(該算法得到的最短路徑長度為15381)。由圖2可以看出,在大致迭代180代后,各代的最短路徑和平均距離保持一致。 圖1 SGO算法chn31最優(yōu)路徑圖 圖2 SGO算法chn31迭代收斂曲線 為了更好地求解TSP問題,本文將基本SGO算法進行了離散化處理。在算法的提高階段和獲得階段分別引入了交叉與變異操作,增加了算法的多樣性,減小了算法整體陷入局部最優(yōu)的可能性。對6個不同的TSP問題進行了仿真試驗,結果證明SGO算法應用在TSP問題上的有效性。但從實驗數據可知,隨著城市規(guī)模的增大,離散SGO算法的性能也隨之降低。因此,如何改進SGO算法來解決大城市規(guī)模問題將是一個新的研究方向。 [參考文獻] [1]Satapathy S, Naik A. Social group optimization (SGO): a new population evolutionary optimization technique[J].Complex & Intelligent Systems, 2016(3):1-31. [2]Naik A,Satapathy S C,Ashour A S,et al.Social group optimization for global optimization of multimodal functions and data clustering problems[J].Neural Computing & Applications,2016:1-17. [3]Lawler E L.The traveling salesman problem:a guided tour of combinatorial optimization[M].Wiley,1985:535-536. [4]Wang Y.The hybrid genetic algorithm with two local optimization strategies for traveling salesman problem[J].Computers & Industrial Engineering,2014(70):124-133. [5]Liu Y H.Different initial solution generators in genetic algorithms for solving the probabilistic traveling salesman problem[J].Applied Mathematics and Computation,2010(1):125-137. [6]程畢蕓,魯海燕,黃洋,等.求解TSP的自適應優(yōu)秀系數粒子群優(yōu)化算法[J].計算機應用,2017(3):750-754. [7]Chen S M,Chien C Y.Solving the traveling salesman problem based on the genetic simulated annealing ant colony system with particle swarm optimization techniques[J].Expert Systems with Applications,2011(12):14439-14450. [8]Liu Yin,Ma Liang.Fuzzy artificial bee colony algorithm for solving traveling salesman problem[J].Application Research of Computers,2013(9):2694-2696. [9]胡中華,趙敏.基于人工蜂群算法的TSP仿真[J].北京理工大學學報,2009(11):978-982.2.3 離散SGO算法的獲得階段
3 求解TSP的離散SGO算法
3.1 參數設置
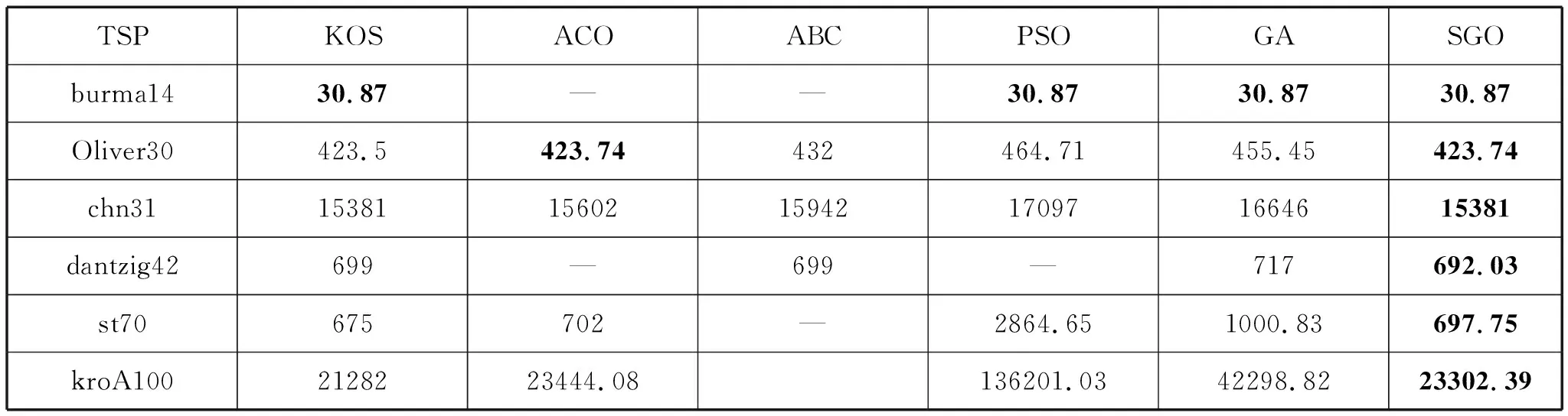
3.2 仿真結果比較
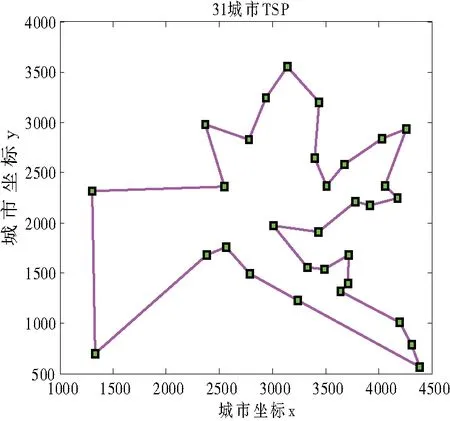
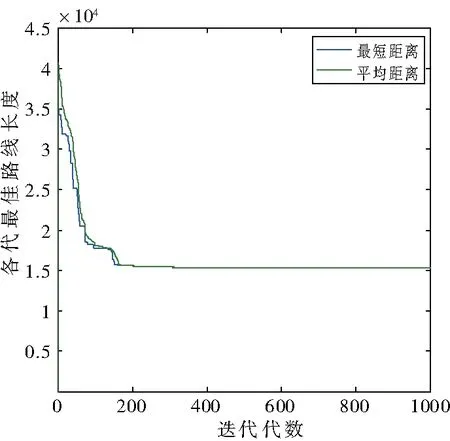
4 結語

