應力敏感性碳酸鹽巖氣藏斜井生產動態規律分析

孟凡坤， 雷 群， 何東博， 閆海軍， 徐 偉

( 1. 中國石油勘探開發研究院，北京 100083； 2. 中國石油西南油氣田分公司 勘探開發研究院，四川 成都 610051 )

0 引言

為提高油氣井產能、改善油氣藏開發效果，斜井、水平井等復雜井型得到廣泛的應用。以開發中的高石梯—磨溪碳酸鹽巖氣藏為例，斜井約占投產井總數的1/2，生產動態呈現高產穩產的變化特征[1]。目前氣藏處于開發早期，對斜井動態變化規律及增產機理認識不清，且儲層應力敏感性較強[2-3]，因此亟需考慮儲層特征，建立斜井數學模型，預測斜井動態變化規律，明確斜井增產機理，從而指導斜井的開發設計。

人們建立多種斜井流動數學模型，模型本質上主要分為三類：一類是以Cinco H等為代表，運用格林函數、Newman乘積等方法，建立實空間斜井數學模型，其理論及計算過程較為簡潔，但未考慮井儲、表皮效應等復雜因素[4-7]；二類為基于傳統的滲流擴散方程，綜合運用Laplace變換、鏡像映射及泊松變換等方法，確立不同邊界條件下的點源函數解，通過數值積分及Stehfest數值反演對斜井模型進行求解，特點是考慮較為復雜的儲層及生產狀況，但推導、計算過程較為復雜[8-13]；三類為在建立斜井滲流模型基礎上，運用有限元等數值方法對模型離散求解，處理過程難度較大，可應用性較差[14-15]。另外，對于應力敏感性的考慮，主要采用數值離散或攝動變換技術進行處理，求解過程復雜，應用條件也較為苛刻[16-21]。

借鑒文獻[22]的研究方法，考慮高石梯—磨溪區塊碳酸鹽巖氣藏儲層滲流特征與邊界特性，基于傳統滲流擴散方程，引入擬壓力及擬時間函數描述滲透率變化規律，綜合運用Laplace變換、Fourier變換及其反變換、點源函數疊加等方法，建立碳酸鹽巖氣藏斜井滲流數學模型；結合氣藏物質平衡方程，對模型進行求解，分析應力敏感因數、井斜角等對生產動態的影響，以指導不同厚度地層井斜角的設計。

1 儲層應力敏感性分析

選取高石梯—磨溪區塊儲層巖心，利用異常高壓巖心驅替裝置，在室溫條件下，開展應力敏感性分析實驗，因裂縫滲透率遠大于基質滲透率，假定測得的巖石滲透率等價于裂縫系統滲透率。在實驗過程中保持圍壓恒定，以5 MPa為間隔逐漸降低內壓，模擬氣藏衰竭式開采過程，測試不同有效應力(凈壓力)時滲透率。定義無因次滲透率(各測試點滲透率與初始測定滲透率之比)，繪制巖心無因次滲透率與有效應力之間的關系曲線(見圖1)。

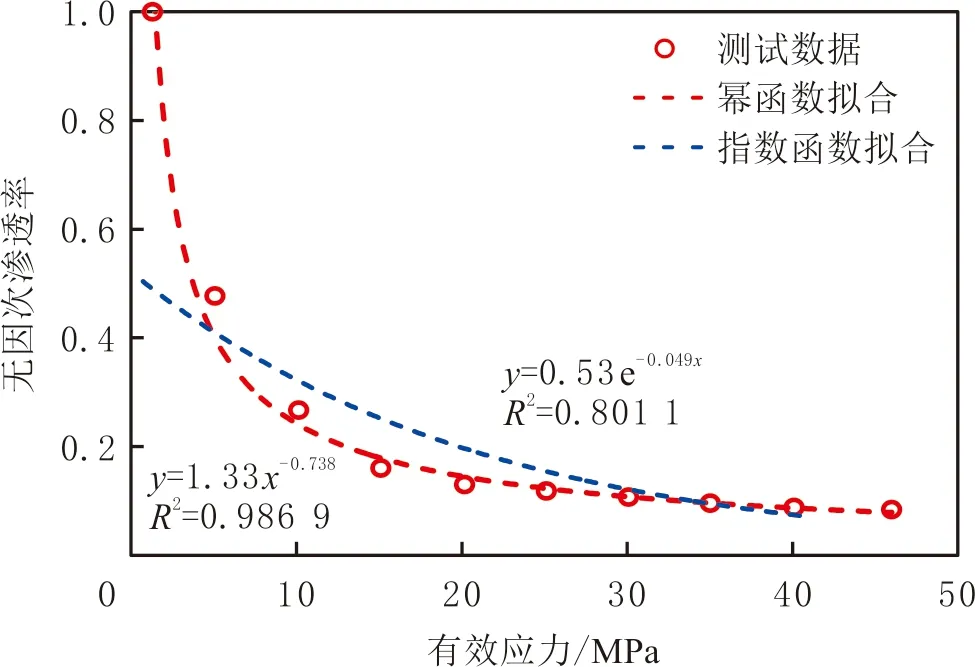
圖1 儲層無因次滲透率隨有效應力變化關系曲線Fig.1 The relation between formation dimensionless permeability and net confining stress

分別運用冪函數與指數函數進行回歸擬合，結果表明冪函數擬合效果較好。根據量綱一致性原則，對回歸公式進行處理[3]，求得無因次滲透率與有效應力變化關系式為

(1)

式中：p為實驗流壓；ps、pi為實驗圍壓與初始流壓；kf為巖石裂縫滲透率；kfi為初始流壓下測定的裂縫系統滲透率；α為儲層應力敏感因數，α=0.738。實驗和實際氣藏開發存在對應關系，氣藏上覆巖層壓力、平均地層壓力及原始地層壓力分別對應實驗圍壓、流壓和初始流壓。

2 模型建立

2.1 物理模型

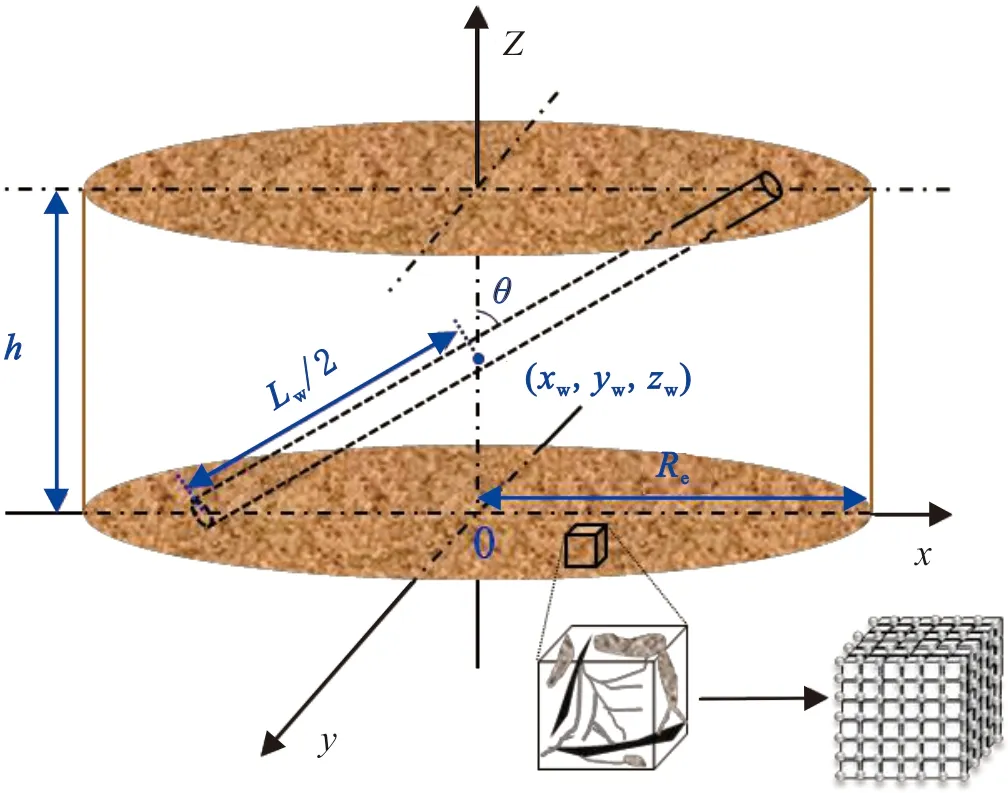
圖2 碳酸鹽巖氣藏封閉邊界斜井模型示意Fig.2 Schematic of a slanted well in carbonate gas reservoir with closed boundary

綜合考慮高石梯—磨溪區塊震旦系氣藏地質特征與開發井型，建立碳酸鹽巖氣藏三重孔隙介質斜井滲流物理模型(見圖2，其中Lw為斜井長度)。

假設：

(1)氣井以恒定產量qg生產，井斜角為θ，完全射開，沿井筒方向氣體流量均勻分布，生產前氣藏中各點壓力相等，等于原始地層壓力pi；

(2)地層水平，統一厚度為h，上下邊界、徑向外邊界封閉，半徑為Re，滿足θ≤arctan(2Re/h)；

(3)基質、溶洞為主要的儲集空間，裂縫為主要的滲流通道，基質向裂縫為擬穩態竄流，裂縫系統滲透率存在應力敏感效應；

(4)考慮氣藏水平與垂直方向裂縫滲透率的各向異性，水平、垂直裂縫滲透率分別為kfh、kfv；

(5)氣體為可壓縮性氣體，忽略巖石及束縛水的壓縮性；

(6)流動為達西滲流，忽略重力、毛管力的影響。

2.2 數學模型

2.2.1 點源數學模型

根據物理模型假設，建立碳酸鹽巖氣藏三重孔隙介質斜井滲流數學模型。先推導滲流數學模型的點源函數解，給出點源模型的基本微分方程、初始條件和邊界條件。

基本微分方程：

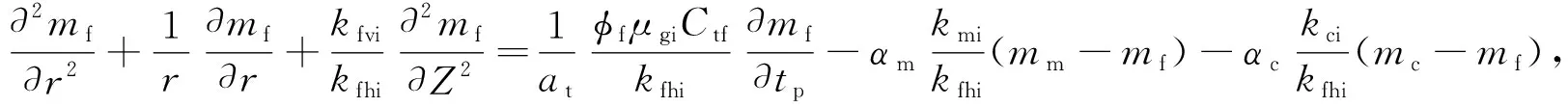
(2)

(3)

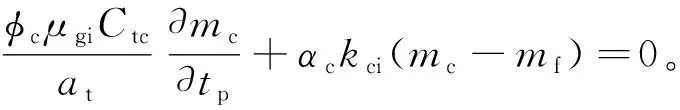
(4)

初始條件：

mf=mc=mm=mpi,tp=0。

(5)

邊界條件：

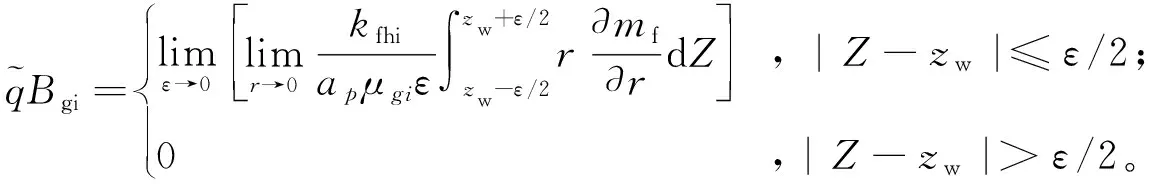
(6)

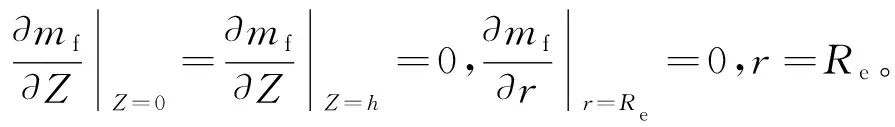
(7)

式(2-7)中：mf、mm、mc、mpi分別為裂縫、基質、溶洞系統及原始地層壓力對應的擬壓力，

(8)

Ctf、Ctm、Ctc分別為裂縫、基質及溶洞系統綜合壓縮系數，

Ctf=Cgi(1-Swfi),Ctm=Cgi(1-Swmi),Ctc=Cgi(1-Swci);

(9)

式(2-7)中存在近似：

(10)

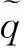
2.2.2 模型無因次化

(11)

(12)

(13)

mcD=mmD=mfD=0,tD=0。

(14)

(15)

(16)

式(11-16)中：rD為無因次半徑；ReD為氣藏無因次半徑；hD為無因次地層厚度；mfD、mmD、mcD分別為裂縫、基質與溶洞系統無因次擬壓力；ωm、ωc、ωf分別為基質、溶洞及裂縫系統儲容比；λm、λc分別為基質、溶洞向裂縫系統的竄流系數。

各無因次變量的定義為

3 模型求解與驗證

3.1 模型求解

3.1.1 斜井無因次擬井底流壓

先對數學模型(式(11-16))進行關于tD的拉氏變換：

(17)

然后引入Fourier變換及其反變換關系式：

(18)

(19)

代入邊界條件，得拉氏空間中的點源函數解為

(20)

(21)

由于產氣量沿斜井段均勻分布，根據連續點源疊加原理，首先對坐標系進行旋轉變換；然后對點源函數解(式(20))沿斜井段積分，得斜井在拉氏空間的無因次壓力為

(22)

(23)

式(17-23)中：s為拉氏變量；LwD為斜井無因次長度；θ、θ′為井斜角和等效井斜角；xD、yD、zD分別為等效壓力點無因次坐標；xwD、ywD、zwD分別為斜井中心點的無因次坐標，表達式為

為了簡化計算，需選擇恰當的等效壓力點，借鑒文獻[4,11-12]的研究方法，等效壓力點無因次坐標設為

(24)

對式(22)進行數值積分，運用Stehfest數值反演方法[23]，可求得無因次井底流壓；有因次化后，可求得擬井底流壓。

3.1.2 斜井井底流壓

由于擬壓力函數考慮氣體性質、儲層滲透率等隨壓力的變化(式(10))，有較強的非線性，因此采用數值積分法構造數值表，通過線性插值確定擬壓力對應的壓力。分別采用Lee-Gonzalez-Eakin半經驗公式法和Hall-Yarbough方法，計算氣體黏度、壓縮因子[24-25]，用式(1)描述滲透率變化。結合物質平衡方程，通過數值積分計算擬時間函數，運用D-A-K方法計算壓縮系數[26]。

數學模型求解步驟為：

(1)計算不同時刻累計產氣量Gp：

Gp=qgt。

(25)

(2)求解物質平衡方程，通過插值求取每一時間步氣藏平均壓力：

(26)

式中：Gsc為氣藏地質儲量，由容積法計算求得。

(3)計算氣體黏度、壓縮系數等PVT參數，根據式(10)計算擬時間tp。

(4)對擬時間進行無因次化，求取無因次井底流壓，有因次化后得到擬井底流壓，通過插值求得實際井底流壓。

3.2 模型驗證

選取高石梯—磨溪區塊兩口投產斜井(X1和X2井)，整理并綜合儲層與生產工藝參數，獲得敏感性分析基礎參數，見表1。天然氣組分測試顯示兩口井的采出氣組成相近，氣體相對密度為0.59，臨界壓力為4.82 MPa，臨界溫度為199.3 K。儲層應力敏感因數由實驗分析和曲線擬合求得，取為0.738。通過井口油壓迭代計算求得井底流壓[27]，將兩口井的實際儲層及流體參數代入文中模型進行計算，與實際生產數據進行對比(見圖3)。

表1 碳酸鹽巖氣藏儲層及生產參數

圖3 文中模型計算結果與實際生產數據Fig.3 Comparison between calculated results and practical data

由圖3可見，兩口井的計算井底流壓與實際井底流壓總體吻合程度較好，驗證文中模型的有效性，表明文中模型可較為準確地描述與預測斜井的生產動態。由圖3(a)可見，在X1井生產初期，計算井底流壓與實際井底流壓之間存在微小差別。原因在于X1井初期實際配產為13×104m3/d，低于計算方案配產(14×104m3/d)，造成計算結果低于實際結果，隨氣井配產提高并保持相對穩定，實際結果與計算結果符合程度變好。

4 參數敏感性分析

儲層特征與井斜角是影響氣井生產動態的主要因素[28]。根據礦場實際，在定產生產條件下，從應力敏感因數、井斜角、地層厚度等方面分析井底流壓的影響規律，確定地層厚度與井斜角之間最佳的匹配關系。

4.1 應力敏感因數

不同應力敏感因數(α為0、0.5、1.0)時，規定最小井底流壓為5.0 MPa，繪制井底流壓隨生產時間變化曲線(見圖4)。由圖4可見，在生產初期，由于采出氣量較少，平均地層壓力下降幅度較小，不同應力敏感因數時裂縫滲透率差值不大，因而各方案井底流壓較為接近；隨開采時間增加，采氣量不斷增大，平均地層壓力下降幅度持續擴大，應力敏感因數越大，裂縫閉合愈嚴重，導致井底流壓遞減速率加快，因而各方案井底流壓的差值不斷增大。當α為1.0、生產時間為950 d時，井底流壓達到設定的最小值而關井；在不考慮應力敏感因數(α=0)時，井底流壓為20.0 MPa，遠高于α為0.5時的井底流壓(約為15.0 MPa)。

4.2 井斜角

不同井斜角θ時氣井井底流壓隨時間變化曲線見圖5。由圖5可見，在生產初期與中期，各方案之間的井底流壓遞減速率較為接近；在生產后期，由于井斜角較小的氣井井底流壓快速降低，高井斜角與低井斜角氣井井底流壓差值劇烈增大。主要在于模型假設流量沿井筒均勻分布，井斜角越大，井筒與地層之間接觸面積越大，在流量恒定條件下，生產壓差越小，井底流壓越高。由于不同井斜角的氣井與地層接觸面積的差值保持恒定，在生產初期與中期，各方案的井底流壓的差值保持穩定；在生產后期，地層能量難以維持設定產量，導致井斜角較小的方案的井底流壓快速降低，各方案之間井底流壓的差值迅速增大。

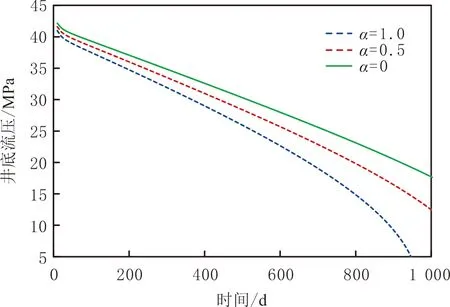
圖4 不同應力敏感因數時氣井井底流壓隨生產時間變化曲線Fig.4 Bottom-hole pressure versus time under different stress-sensitive coefficients

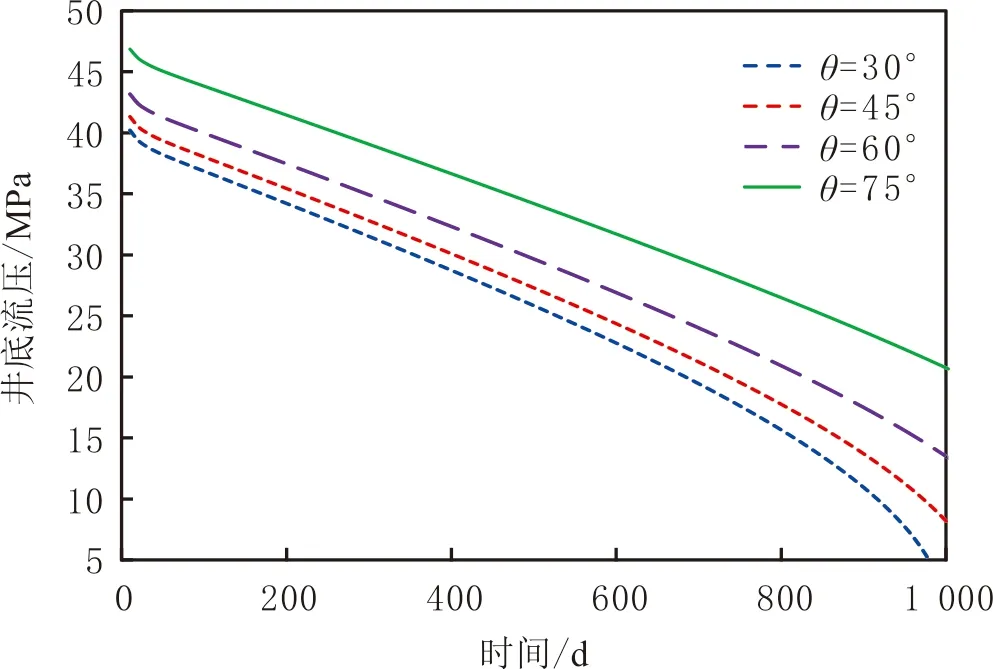
圖5 不同井斜角時氣井井底流壓隨生產時間變化曲線Fig.5 Bottom-hole pressure versus time for different inclined angles

4.3 地層厚度

碳酸鹽巖氣藏非均質性強，同一層系不同位置地層厚度差異較大。保持井斜角恒定，繪制不同地層厚度h時氣井井底流壓隨時間變化曲線(見圖6)。由圖6可見，由于地層厚度越大，井筒與地層接觸面積越大，在產量恒定的條件下，生產壓差越小，井底流壓越高，呈某一時刻井底流壓隨地層厚度的增加而增大的變化趨勢。地層厚度與某一時刻井底流壓之間存在非線性關系，即隨地層厚度的不斷增大，井底流壓增加量逐漸減小，表現為井底流壓曲線相互接近。

由圖5-6可見，對于某一厚度地層，井底流壓隨井斜角的減小而降低，但減少量不斷減小，存在某一井斜角使井底流壓保持在較高的水平(見圖5)；當井斜角恒定時，井底流壓隨地層厚度增加而升高，但增加量逐漸減少，存在某一地層厚度使井底流壓保持相對穩定(見圖6)。為明確地層厚度與井斜角之間的變化關系，設定不同井斜角、地層厚度，繪制氣井生產100 d后井底流壓隨地層厚度變化曲線(見圖7)。

由圖7可見，對于某一特定井斜角氣井，井底流壓隨地層厚度的增加而增大，初始上升速率較快，后期較為平緩，存在最優的地層厚度與之匹配，且井斜角越大，與之匹配的最優地層厚度越小。反之，當氣藏地層厚度已知，在某一生產時刻或時間段內，必存在唯一的井斜角使井底流壓維持在相對穩定的水平。

圖6 不同地層厚度時氣井井底流壓隨生產時間變化曲線Fig.6 Bottom-hole pressure versus time for different formation thickness

圖7 不同井斜角時氣井生產100 d后井底流壓隨地層厚度變化曲線Fig.7 Correlation chart between formation thickness and bottom-hole pressure for different inclined angles on the 100th day

5 結論

(1)考慮儲層地質特征與應力敏感性，建立碳酸鹽巖氣藏三重孔隙介質封閉邊界斜井流動數學模型，通過與礦場實際生產數據的對比，驗證模型的有效性，為生產動態分析和預測奠定基礎。

(2)儲層應力敏感效應隨生產時間增加而影響程度愈發顯著，大幅縮短氣井的穩產時間；在生產初期與中期，不同井斜角時井底流壓有近似相同的遞減速率，在生產后期井底流壓差值迅速擴大，井斜角、地層厚度越大，氣井穩產時間越長。

(3)對于某一厚度儲層，存在唯一最優的井斜角，在某一生產時刻或時間段內井底流壓保持相對穩定，可以為不同厚度碳酸鹽巖儲層井斜角的設計提供參考。

參考文獻(References):

[1] 王文之,楊躍明,張璽華,等.四川盆地震旦系燈影組儲層特征及成因[J].東北石油大學學報,2016,40(2):1-10.

Wang Wenzhi, Yang Yueming, Zhang Xihua, et al. Reservoir characteristics and genesis of the Sinian Dengying formation in Sichuan basin [J]. Journal of Northeast Petroleum University, 2016,40(2):1-10.

[2] 徐新麗.含微裂縫低滲儲層應力敏感性及其對產能影響[J].特種油氣藏,2015,22(1):127-130.

Xu Xinli. Stress sensitivity of low-permeability reservoir containing micro-fracture and its influence on productivity [J]. Special Oil & Gas Reservoirs, 2015,22(1):127-130.

[3] 孟凡坤,雷群,閆海軍,等.高石梯—磨溪碳酸鹽巖氣藏斜井產能評價[J].特種油氣藏,2017,24(5):111-115.

Meng Fankun, Lei Qun, Yan Haijun, et al. Deliverability evaluation for inclined well in Gaoshiti-Moxi carbonate gas reservoir [J]. Special Oil & Gas Reservoirs, 2017,24(5):111-115.

[4] Cinco H, Miller F G. Unsteady-state pressure distribution created by a directionally drilled well [J]. Journal of Petroleum Technology, 1975,27(11):1392-1400.

[5] Abbaszadeh M, Hegeman P S. Pressure-transient analysis for a slanted well in a reservoir with vertical pressure support [J]. SPE Formation Evaluation, 1990,5(3):277-284.

[6] 李巍,盧德唐,王磊,等.復雜邊界斜井試井分析方法研究[J].油氣井測試,2009,18(6):1-5.

Li Wei, Lu Detang, Wang Lei, et al. A transient pressure solution for inclined wells with complex boundaries [J]. Well Testing, 2009,18(6):1-5.

[7] 王海靜,仝興華,薛世峰,等.板狀油藏大斜度井流入動態[J].中國石油大學學報:自然科學版,2011,35(6):88-94.

Wang Haijing, Tong Xinghua, Xu Shifeng, et al. Inflow performance of highly deviated well in slab reservoir [J]. Journal of China University of Petroleum: Edition of Natural Sciences, 2011,35(6):88-94.

[8] Ozkan E, Raghavan R. New solutions for well-test analysis problems, part 1: Analytical considerations [J]. SPE Formation Evaluation, 1991,6(3):359-368.

[9] Ozkan E, Raghavan R. New solutions for well-test-analysis problems, part 2: Computational considerations and applications [J]. SPE Formation Evaluation, 1991,6(3):369-378.

[10] Ozkan E. New solutions for well-test-analysis problems: Part Ⅲ-additional algorithms [R]//SPE 69th Annual Technical Conference and Exhibition. Society of Petroleum Engineers, 1994.

[11] Ozkan E, Raghavan R. A computationally efficient, transient-pressure solution for inclined wells [J]. SPE Reservoir Evaluation & Engineering, 2000,3(5):414-425.

[12] Wang Haitao, Zhang Liehui, Guo Jingjing, et al. An efficient algorithm to compute transient pressure responses of slanted wells with arbitrary inclination in reservoirs [J]. Petroleum Science, 2012,9(2):212-222.

[13] 廖新維.雙重介質擬穩態油藏斜井試井模型研究[J].石油勘探與開發,1998,25(5):57-61.

Liao Xinwei. Discussion of slanted well test model in dual-porosity reservoirs with pseudo steady state flow [J]. Petroleum Exploration & Development, 1998,25(5):57-61.

[14] Khatteb H A, Yeh N S, Agarwal R G. Pressure transient behavior of slanted wells in single and multiple-layered systems [R]//SPE 66th Annual Technical Conference and Exhibition. Society of Petroleum Engineers, 1991.

[15] 楊志興,楊明,劉海成,等.低滲變形介質油藏斜井試井及現場應用[J].科學技術與工程,2014,14(21):81-88.

Yang Zhixing, Yang Ming, Liu Haicheng, et al. Deviated well test in low permeability reservoirs with deformational media [J]. Science Technology and Engineering, 2014,14(21):81-88.

[16] Chin L Y, Raghavan R, Thomas L K. Fully coupled analysis of well responses in stress-sensitive reservoirs [J]. SPE Reservoir Evaluation & Engineering, 2000,3(5):435-443.

[17] Raghavan R, Scorer J D T, Miller F G. An investigation by numerical methods of the effect of pressure-dependent rock and fluid properties on well flow tests [J]. Society of Petroleum Engineers Journal, 1972,12(3):267-275.

[18] 張磊,同登科,馬曉丹.變形三重介質三滲模型的壓力動態分析[J].工程力學,2008,25(10):103-109.

Zhang Lei, Tong Dengke, Ma Xiaodan. Pressure dynamic analysis of triple permeability model in deformed triple porosity reservoirs [J]. Engineering Mechanics, 2008,25(10):103-109.

[19] Kikani J, Pedrosa O A. Perturbation analysis of stress-sensitive reservoirs [J]. SPE Formation Evaluation, 1991,6(3):379-386.

[20] 王文環.應力敏感砂巖地層三區復合凝析氣藏不穩定試井模型[J].石油勘探與開發,2005,32(3):117-119.

Wang Wenhuan. Three-zone composite well test model of condensate gas reservoir in stress-sensitive sandstone [J]. Petroleum Exploration & Development, 2005,32(3):117-119.

[21] 寧正福,廖新維,高旺來,等.應力敏感裂縫性雙區復合氣藏壓力動態特征[J].大慶石油學院學報,2004,28(2):34-36.

Ning Zhengfu, Liao Xinwei, Gao Wanglai, et al. Pressure transient response in deep-seated geothermal stress-sensitive fissured composite gas reservoir [J]. Journal of Daqing Petroleum Institute, 2004,28(2):34-36.

[22] 任俊杰,郭平,汪周華.三重介質油藏斜井壓力動態特征分析[J].水動力學研究與進展,2012,27(1):7-15.

Ren Junjie, Guo Ping, Wang Zhouhua. Dynamical characteristics analysis of inclined well in triple medium reservoir [J]. Chinese Journal of Hydrodynamics, 2012,27(1):7-15.

[23] Stehfest H. Algorithm 368: Numerical inversion of Laplace transforms [J]. Communications of the ACM, 1970,13(1):47-49.

[24] Lee A, Gonzalez M, Eakin B. The viscosity of natural gases [J]. Journal of Petroleum Technology, 1966,18(8):997-1000.

[25] Hall Kenneth R, Lyman Yarborough. A new equation of state forZ-factor calculations [J]. Oil and Gas Journal, 1973,71(7):82-92.

[26] Dranchukp M, Purvisr A, Robinson D B. Computer calculation of natural gas compressibility factors using the Standing and Katz correlation [M]. Edmonton: Petroleum Society of Canada, 1973.

[27] 李士倫.天然氣工程[M].北京:石油工業出版社,2008:112-127.

Li Shilun. Natural gas engineering [M]. Beijing: Petroleum Industry Press, 2008:112-127.

[28] 李紀,李曉平.不同井型下氣井產能對比研究與評價[J].特種油氣藏,2016,23(2):108-111.

Li Ji, Li Xiaoping. Productivity comparison and evaluation of gas wells with different well-types [J]. Special Oil & Gas Reservoirs, 2016,23(2):108-111.