基于Gamma隨機過程的水工鋼閘門時變可靠度方法

徐衛敏,盧鵬程,范興朗

XU Weimin，LU Pengcheng，FAN Xinglang

(1.浙江建設職業技術學院,浙江 杭州 311231；2.浙江科技學院,浙江 杭州 310023；3.浙江工業大學建筑工程學院,浙江 杭州 310014)

結構在服役過程中,由于受荷載作用、材料內部作用和環境作用等因素影響,往往會引起其結構抗力和剛度的退化,從而帶來正常服役可靠度的降低[1]。對于水工鋼閘門結構而言,影響其抗力和剛度的最重要因素是鋼板的銹蝕[2-3]。因此,為了預測現役鋼閘門結構在未來使用期內的壽命,必須了解鋼板的銹蝕規律,從而掌握其抗力和剛度隨時間的變化規律。

引起鋼板銹蝕的因素眾多,主要有周圍環境含有的腐蝕性物質(空氣中的SO2含量等)、水中的酸堿性物質和腐蝕微生物等。另外,當鋼閘門所處不同地理位置時,受當地風速、溫度、泥沙以及水流流速等因素影響,其腐蝕程度也是不同的。文獻[4]對收集國內水工鋼閘門銹蝕檢測的數據,確定了現役鋼閘門銹蝕速率的概率分布模型。研究結果表明我國水工鋼閘門銹蝕速率的均值和變異系數分別為0.034mm/a和0.43。文獻[5]對部分工程實測數據的統計數據表明,銹蝕速率均值的變化范圍為0.015～0.07mm/a,變異系數的變化范圍為0.37～0.88。

在對已有鋼閘門結構進行評估和維修規劃時,考慮服役過程中承載力的退化規律是非常重要的。目前國內外學者已經對此進行了研究，Mlakar和Bryant[6]分析了平面鋼閘門均勻腐蝕引起構件厚度減小時的可靠度。Patev等[7]在考慮腐蝕損傷對鋼材屈服強度影響的基礎上,分別采用了時變可靠性分析方法和危險函數方法分析了鋼閘門的時變可靠度。周建方等[5]在總結閘門構件銹蝕規律的基礎上對衰減函數為確定性函數和隨機變量的情況鋼閘門結構的時變可靠度進行了分析。研究結果表明,當衰減函數為確定性函數時,其計算結果偏于不安全。李典慶和常曉林的綜述文章[7]對這方面的研究做了較為全面的總結。

從以上研究結果可以看出,盡管已有研究通過衰減函數考慮了鋼板銹蝕對鋼閘門承載力退化的影響,但是該函數并未考慮結構在演化過程中的時變隨機性。實際上,鋼板銹蝕的過程是一個隨機累積的過程,相應的抗力衰減函數應該通過隨機過程進行模擬。基于此,本文根據鋼板銹蝕過程的基本特點,通過Gamma隨機過程對銹蝕過程進行模擬,提出了一個基于退化的時變可靠度分析方法。

1　鋼板銹蝕過程模擬及參數估計

實際工程中,影響水工鋼閘門鋼板銹蝕的因素眾多,主要有銹蝕時間、銹蝕速度等,且這些因素大多具有不確定性。在數據較易獲得的情況下,可以將各個因素處理為隨機變量,并通過所得到的數據獲得這些隨機變量的分布類型和統計參數,然后采用Monte-Carlo的方法確定鋼板銹蝕量的統計參數。對于大多數工程,獲取這些數據難度較大,本文采用Gamma隨機過程模擬鋼板銹蝕深度。

Gamma隨機過程是一種考慮獨立、非負退化增量的隨機過程,適合模擬具有微小增量的累積漸變過程,如疲勞、徐變和銹蝕等[9]。該過程可通過形狀參數和尺度參數進行描述。

假定{d(t),t≥0}為一個隨機Gamma過程,其概率密度函數可以表達為：

(1)

式(1)中:Gamma隨機過程具有如下性質[10]：

1)d(0)=0；

2)對于任意的τ>t≥0,增量d(τ)-d(t)服從Gamma分布,即:

d(τ)-d(t)～Ga[α(τ)-α(t),λ].

(2)

3)d(t)是一個獨立增量過程,即對于任意t12),各增量d(t2)-d(t1),…,d(tn)-d(tn-1)相互獨立。

根據Gamma過程的性質,銹蝕量d(t)的平均值和方差可以表示為：

(3)

(4)

(5)

鋼板銹蝕量可以通過改變Gamma過程形狀參數α(t)來表征其隨時間的變化規律。一般來說,α(t)可以表達成關于時間t的冪函數形式[1]：

α(t)=ctb.

(6)

對于特定的退化過程,通常可以根據相應的工程知識來確定相應的退化過程曲線形狀參數。文獻[11]列出了幾種常見的退化過程參數b的值。本文取b為1.0。

對鋼閘門結構進行可靠度評估時,當鋼板銹蝕量數據足夠時,形狀函數α(t)中的參數c和Gamma過程的尺度參數λ可以采用最大似然估計法或者矩估計法進行確定[12]。但是對于大多數水工鋼閘門而言,由于對結構某個區域連續監測或者歷時較短的檢測較難進行,本文主要通過已有銹蝕率的統計參數對進行參數c和λ進行反向標定得到。事先假定參數λ為某個固定值,根據式(3)并結合參數λ即可確定參數c。

確定參數后,銹蝕累積量可用下列順序采樣方法進行模擬[13]：

1)t=0,d0=0；將總時間T等分為n個子區間；

2)當t=ti時,產生服從Gamma分布函數Ga(α(ti)-α(ti-1),λ)的隨機數Δdi,該隨機數即為時段ti-ti-1內產生的銹蝕增量。ti時刻銹蝕累計量

di=di-1+Δdi;

3)重復過程2)直到達到總時間T為止。

2　時變可靠度計算方法

服役過程中由于各種環境因素會導致抗力退化,因此結構抗力R(t)是一個隨時間遞減的隨機過程。目前國內外研究者通常將抗力R(t)表示為如下形式[14-15]：

R(t)=R0φ(t).

(7)

式(7)中：R0為初始時刻的抗力隨機變量；φ(t)為抗力退化因子,當不考慮維修過程時,它是從1開始單調遞減的。根據處理方式不同,φ(t)可以表示為確定函數和隨機過程兩種形式。

對于水工鋼閘門結構,在初始厚度相同的情況下,φ(t)可以寫成[5]：

(8)

式(8)中:D0表示鋼板初始厚度。當構件各部分鋼板厚度不同時,表達式相對較復雜。

結構的功能函數可以表示為:

Z=R(t)-S(t).

(9)

其中,R(t)和S(t)分別表示為結構的抗力與荷載效應,它們都是隨機過程。根據可靠度的定義,在服役期間[0,T]內,結構失效的概率可以表示為

pf=1-Pr{R(t)>S(t)|?t∈[0,T]}.

(10)

一般情況下,式(10)很難通過解析方式求解得到。因此,本文采用Monte-Carlo方法進行模擬求解。具體模擬過程如下：

1)給定鋼板初始厚度d0、鋼板銹蝕速率統計特征和服役時間T,確定Gamma過程統計參數；

2)根據抗力變量分布類型生成承載力初始值R0的一個樣本值r0；

3)將服役時間T劃為n個等子區間[t0,t1],[t1,t2],…，[tn-1,tn],根據Gamma過程分別計算t1，t2，…，tn時刻對應的銹蝕量d(ti),其中ti=iT/n,i=1,2,3,…,n；

4)根據荷載分布類型生成服役期T內n個荷載樣本值si,i=1,2,3,…,n；

5)分別計算服役期內ti時刻對應的承載力r(ti)=r0φ(ti),其中ti=iT/n。如果對于i=1,2,3,…,n均有r(ti)≥si成立,則此次模擬結構安全；否則,結構失效；

重復步驟2)～5)直到滿足模擬精度。若最終模擬次數為N,失效次數為M,則結構可靠度可近似采用nf=M/N表示。

3　數值算例及討論

計算某水工鋼閘門結構某構件在服役期T= 50 a內的結構可靠度。其承載力極限狀態方程為：

Z=R-SW-SQ=0.

(11)

其中,R=φ(t)R0,R0為承載力初始值；SW和SQ分別為靜水壓力和其他活荷載對應的荷載效應。、SW和SQ的設計值存在如下關系：

R0K=1.5(SWK+SQK).

(12)

為后續計算方便,假定SWK=1.0,SQK/SWK=0.1,R0、SW和SQ的分布類型和統計參數分別見表1。

表1　隨機變量統計參數和分布類型

計算中,事先假定參數λ為0.5,參數c通過銹蝕率計算得到。計算中考慮了三種不同銹蝕率(0.03mm/a、0.05mm/a和0.07mm/a),及三種不同的鋼板初始厚度(20mm、25mm和30mm)和不同的衰減函數形式確定函數形式和Gamma隨機過程。

圖1表示三種不同銹蝕速率時鋼閘門時變可靠度變化情況。從圖1可以看出,當銹蝕速率為0.07mm/a時,經過50年服役期,可靠度從3.92降低為1.73。銹蝕速率越大,可靠度降低越多,且隨著服役年限增大可靠度降低越多。

圖1　不同銹蝕率條件時變可靠度變化情況

圖2表示為三種不同初始板厚時鋼閘門時變可靠度變化情況。從圖2可以看出,當鋼板初始厚度為25mm時,經過50年服役期,可靠度從3.92降低為2.06。當鋼板初始厚度從20mm變化到30mm時,在T為50年時,可靠度變化0.45,變化幅度較銹蝕速率緩慢。

圖2　不同初始厚度條件時變可靠度變化情況

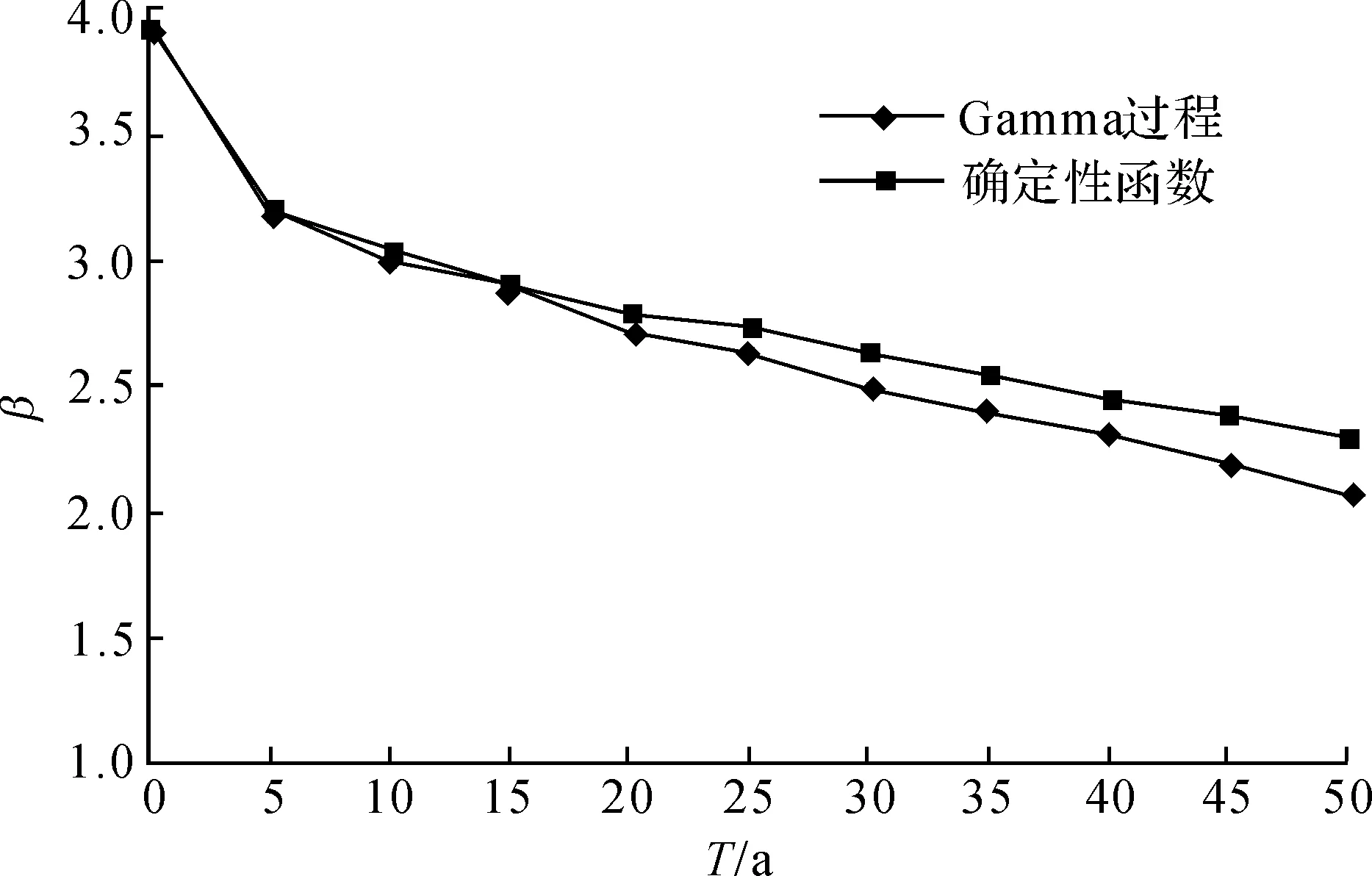
圖3　不同衰減函數條件時變可靠度變化情況

圖3比較了采用確定性衰減函數和Gamma退化過程時鋼閘門時變可靠度的變化情況。從圖3可以看出,在服役壽命早期,采用兩種形式對可靠度計算結果影響不大；當服役壽命超過30年后,兩者差別逐漸加大,且采用確定性衰減函數計算時計算結果偏于不安全,這是與文獻[5]的結論相一致的。

4　結　語

鑒于目前正在運行的鋼閘門有許多已經達到或超過了規范規定的折舊使用年限,故對在役鋼閘門進行剩余壽命預測并進行加固維修勢在必行。如何考慮由于鋼板銹蝕引起鋼閘門結構抗力退化進而導致結構可靠度降低是剩余壽命預測中的關鍵問題。本文根據鋼閘門鋼板銹蝕微小累積性和隨機性的特點,采用Gamma隨機過程對鋼板銹蝕量進行了模擬,進而得到衰減函數的隨機過程表達式,采用Monte-Carlo法對鋼閘門結構時變可靠度進行了計算。研究結果表明：

1)相比于目前使用的衰減函數確定性函數和隨機變量模型,本文將之擴展至隨機過程模型。計算結果表明,采用確定性函數形式進行時變可靠度計算結果偏于不安全。

2)減小初始板厚度和增大銹蝕速率均可引起可靠度降低,且隨著服役年限增大可靠度降低越多。相比于初始板厚度,銹蝕速率對時變可靠度的影響更大。