中國傳統紋樣在現代服飾中的設計實踐
郭 影,汪思佳,鄭 婷,秦 芳,張海晨,張小卉
(金陵科技學院 藝術學院,江蘇 南京211169)
傳統紋樣作為中國傳統文化中不可或缺的一部分,一直被人們用來表達不同的祈愿。尤其是在物質生活豐富的當代,傳統紋樣不僅能滿足人們精神層面的需求,同時也能滿足人們對于服裝審美的需求。紋樣的起始可追溯到商周時期的青銅器紋,當時出現的龍紋寓意著吉祥和尊貴,是華夏子孫的守護神獸。中國傳統紋樣發展于唐宋時期并盛行于唐代,當時出現了忍冬、牡丹等不同的花草紋樣,在經過波形曲線的結構形式處理后排列組合而成,寓意生機勃勃。明清時期多見組合圖案紋飾,以畫面形式寄托寓意,圖必有意,意必吉祥。
1 中國傳統紋樣的發展歷程及研究價值
中國傳統紋樣大多來自民間,經歷了數千年的沉淀,反映出華夏民族的民間藝術和風俗文化。而紋樣的發展也是一個逐漸深入的過程,是人類文化從低級到高級,從簡樸到豐富的過程[1]。從殷商時期出現大量龍紋的青銅器紋飾開始,到戰國時期多采用更具有藝術表現力的對稱、連續等方式出現的傳統紋樣;再到秦漢時期,充滿人類想象力和創造力的紋飾以抽象的方式出現(圖1);再到隋唐時期,紋樣表現以團花紋為主要形式(圖2);再到宋元時期,傳統紋樣轉為清雅、婉約的寫實風格,隨處可見幾何圖案的紋飾(圖3)。回紋是幾何紋樣中比較有代表性的一種,回紋的線條大多呈方形,沿邊緣有規律地進行曲折卷曲,象征富貴連綿不斷,常做邊緣裝飾之用。到明清時期,傳統紋樣以組合形式的圖案出現,并與節日開始聯系起來,總體趨于成熟。直到現代,傳統紋樣形式萬千,造型百態。
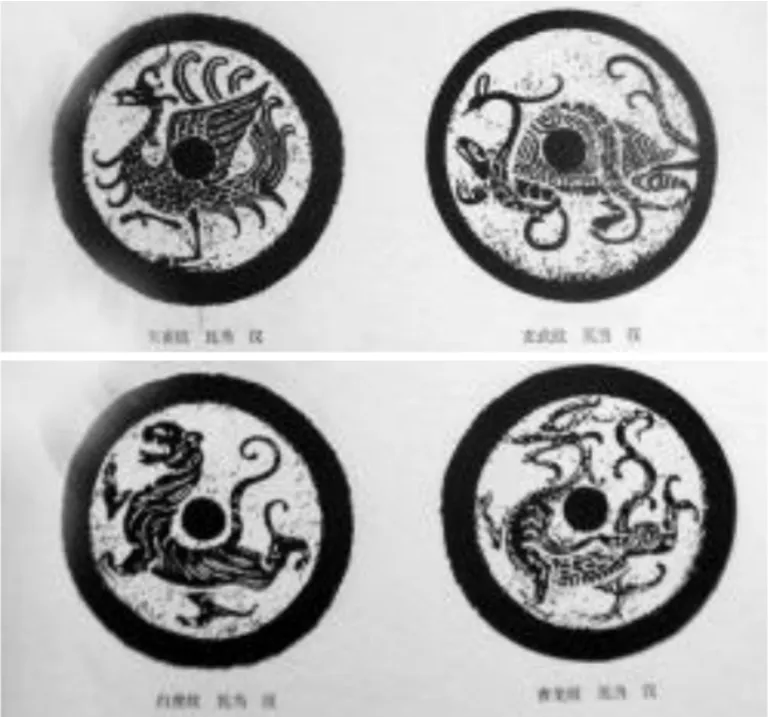
圖1 秦漢時期瓦當紋樣
隨著歷史的進程不斷演變,傳統紋樣不僅是人們表達美好愿望的載體,更代表著一個民族不斷積累和沉淀的藝術結晶,是無價的瑰寶。作為服裝設計師應該挖掘傳統紋樣的象征意義,創造出具有中國文化特色的服裝設計作品,讓傳統紋樣得到廣泛傳播,讓更多的人意識到傳統文化的重要性。

圖3 宋代回紋陶碗
2 中國傳統紋樣在現代服飾設計上的應用
2.1 應用形式
傳統紋樣發展歷史悠久,紋樣本身及其組合形式多種多樣,相較其他紋樣而言略顯復雜,現代服裝設計為了能夠大批量生產且便于傳播,普遍采用簡單明了的圖案紋樣,講究實用性大于設計性。現代應用紋樣也不適合過滿,應局部應用,以單獨紋樣的形式出現比較好。傳統紋樣在進行變形設計時,可以保留大致輪廓,對細節進行刪繁就簡或是概括抽象。在當前的服裝設計中,可以根據圖案的設計目的和現代服飾的造型審美特點進行分解組合,將圖案的組成要素分開來,制作成系列性的產品,使其具有創意的同時不失本真[2]。
一般單獨式的構成是采用獨立的形體構成,其自身可以作為裝飾的主體,且沒有外輪廓的限制,作為圖形的最小單位,也可以作為構成后者連續圖案的基本單位,在構圖中的應用非常靈活[3]。不同的服裝款式需要與特定的傳統紋樣類型進行搭配(圖4)。具體而論,寬松的服裝款式,整體空間面積較大,傳統紋樣若是過小,會顯得服裝不倫不類、小家子氣,相較而言可以選擇風格更大氣、顏色更明快的傳統紋樣,而且需要貼近服裝主基調,才能更加協調。對于貼身的服裝款式來說,容易體現人體形態,圖案過大,會顯得人體形態不協調,需要選擇與人體形態相協調、較小一點的傳統紋樣,做到既要適合人體結構形態,又要突出表達且不流于形式、主次分明。這需要對傳統紋樣有一定的了解,并且進行服裝上的實驗,掌握經驗,才能得心應手地運用傳統紋樣。
通過分析傳統紋樣的發展歷程、工藝技法,結合現代服裝設計中傳統紋樣的實際運用形式,可以幫助我們探索傳統紋樣在服裝設計領域未來的發展方向。突破傳統、局限的理念,結合現代設計元素,為傳統紋樣產生無限的空間。

圖4 不同服裝款式與傳統紋樣的搭配
2.2 工藝表現
在服裝上裝飾傳統紋樣,不僅能豐富服裝的整體設計造型,還能給面料帶來不同的肌理效果。將傳統紋樣與不同質感的服裝進行有機融合,如刺繡、印花的傳統紋樣局部肌理與面料主體不一樣,能產生意想不到的造型效果。相較于棉、麻、絲綢等傳統面料與傳統紋樣結合頗顯質樸,現代合成纖維材料與傳統紋樣結合更加時尚,符合潮流。
在現代服裝設計中,除了刺繡、盤扣、釘珠、手繪、染印等傳統手工藝可以在織物表面進行傳統紋樣的處理,很多現代工藝技術也可以在織物表面處理傳統紋樣,例如面料的藝術再造、印花等現代工藝技術(圖5)也可以實現其獨特的裝飾效果。由于成本低、制造快的特點,印花在現代服飾圖案工藝表現中是最常見的。不僅如此還可以對傳統紋樣的結構和框架進行適當的破壞和刪減,以達到更好的裝飾效果。

圖5 傳統與現代工藝技術
2.3 運用價值
中國作為一個服裝產業大國,其服裝的文化、觀念以及設計越來越備受世界的矚目。中國服裝設計已從單純的產品設計轉向強調市場意識、創新能力和品牌能力的綜合性產業鏈,遵循創新與繼承相結合,挖掘中國元素的設計表達方法,將傳統服裝的優點和現代時尚元素緊密結合并發揚光大,同時激勵服裝品牌發展戰略的構建[4]。
中國設計應該是向內看,向東方看。我們自身的文化需要我們自己來挖掘,必須要花精力去研究中國文化,這也是對世界的一種貢獻[5]。近年一帶一路的提出,帶動了我國與周邊各國的經濟貿易,社會發展越來越好,提升了國民的生活質量。如今中國國力強大,提及中華民族的傳統文化,民族自豪感油然而生,也使傳統紋樣在國內市場有了更好的表現。
隨著世界經濟的快速發展和科技的日新月異,服裝背后的個性和民族意義得到更多的重視,設計文化逐步形成一個更加開放的大染缸,不同的文化在這里融合、重鑄、新生。具有東方文化的服飾設計開始登上世界時裝的舞臺,不僅是本土的服裝設計師,西方的服裝設計師也開始對東方元素感興趣,各種風格的服裝作品如雨后春筍般駐扎在時尚的鎂光燈下,競相爭艷。而且,在現代服飾設計中充分地融入傳統紋樣具有一定的現實意義和實用性,不僅可以滿足人們對設計的多元層次要求,也可以使中國的傳統文化得以傳承,讓現代設計在保持時尚美感的同時又體現出中國濃厚的民族特征[6]。
蓋婭傳說是近年比較具有代表性的中國風高級成衣品牌新秀,由中國著名服裝設計師熊英女士創立,僅僅用2年時間就走上了中國國際時裝周,3年時間就在巴黎時裝周的舞臺上大放異彩。蓋婭傳說將傳承中國傳統文化作為品牌的基石,希望能將中國風韻時裝推向國際舞臺。想要利用“中國元素”打入服裝市場,不僅要追趕國際大牌的步伐,還要和眾多像黑馬一樣異軍突起的本土品牌競爭。可以說,誰能準確敏銳地把握“中國元素”的新變化和新運用,誰就可以占領未來的消費市場。
3 中國傳統紋樣在本設計中的應用實踐
3.1 設計靈感來源與構思
本系列設計作品的靈感來自于對中國傳統紋樣的了解及探索,在深入接觸的過程中迸發了將云紋、鶴紋這2種典型的傳統紋樣通過現代設計手法的形式表達在作品中的想法(圖6)。云紋作為中華民族經典的傳統紋樣之一,是中國非物質文化遺產的一部分,其包含的文化內涵和美學意味根植在深厚的民族文化沃土中。鶴是中國傳統紋樣中的經典形象,人們常將它與其他紋樣組成新的圖案,借此來抒發內心的情感與愿望,表達人們祈求福壽安康以及對美好生活的向往。

圖6 云紋與鶴紋
因此,本系列設計的主題為“承·祥”,主要圍繞中國傳統紋樣——云紋與鶴紋,旨在通過創新設計來表達中國傳統紋樣在現代服飾設計中的藝術美感。通過對傳統紋樣的靈活運用,將千百年來傳承的傳統文化表達在設計作品中。最終結合傳統紋樣的圖片和文獻,并查找歷年傳統紋樣元素在現代服飾設計上應用的優秀作品,體會傳統紋樣與現代服飾設計相融合的韻味,成功將云紋與鶴紋元素運用在現代時尚設計中,做出了既有時尚感又有文化底蘊的現代服裝。
3.2 設計實踐的具體分析
本系列設計通過對傳統云紋以及鶴紋寓意和內涵的探索,對傳統云紋紋樣與鶴紋紋樣的結構進行提煉和再設計,主要采用云紋紋樣中的曲線元素以及其多變的形式與鶴紋紋樣中鶴所表現的優雅形態,采用面料再造、機器印花、手工刺繡等多種表現手法對云紋與鶴紋做抽象、概括形式的表達。借用云紋流暢優美的曲線和柔和的色彩與鶴紋蘊含的美好傳統文化,使設計的服裝符合現代女性優雅神秘的感覺。所以,將傳統紋樣加入到現代服裝設計里面,不僅增加了服飾的美觀性,也植入了很深的文化底蘊[7]。
從材料選擇來看,傳統云紋樣線條彎曲流暢,流動感非常強,再考慮到生活中的云,也是造型多變,縹緲虛幻。因此,要想同時滿足云紋既彎曲流暢又縹緲虛幻的特點,面料必須要輕薄可透,視覺上有延伸的感覺,所以紗是首選面料(圖7)。而傳統鶴紋樣常常以優美的姿態出現,多采用刺繡與印花的方式來表現,因此,面料更傾向于具有一定挺括度,便于印花與手工刺繡的面料。在綜合考慮了材質對比與可實施度之后,最終選擇了針織錦棉羅馬布(圖8)。

圖7 輕薄可透的歐根紗面料
在本系列設計中,選擇白、灰、黑、暗紅色為服飾設計的主色調,在色彩上打破傳統以五色為主要用色的觀點,色彩的選擇上與當代色彩流行趨勢相結合,充分考慮服裝色彩與款式之間的關系,讓設計盡量做到與現代時尚感和諧統一,更加符合當代人的審美標準。另外以這幾種顏色為主色調,除了削弱了傳統紋樣的固用色彩體系,同時也達到了現代人在色彩情感上的滿足,促進了云紋元素與鶴紋元素在現代服飾設計上存在更廣闊的空間。白與灰,黑與暗紅,色彩之間壓制,削弱了最亮與最暗的對比關系,使服裝整體呈現出優雅、高貴、大氣的感覺,增加了本系列服裝設計的層次感與時代感。

圖8 具有一定挺括度的羅馬布面料
工藝上,則選擇了面料再造、手工刺繡與機器印花3種工藝手法。面料再造主要運用在云紋的表現上,要將云紋造型多變、縹緲虛幻的特點表現出來,所以選擇將面料層層堆積,并通過做圓版的方式來進行面料裁剪(圖9),依此所形成的云紋能夠形成優美流暢的弧線與云層的視覺效果(圖10)。手工刺繡主要運用在鶴紋的表現手法上,因為鶴紋動態較復雜,所以提煉其動作的最基本姿勢,進行簡易的手工刺繡,刺繡手法主要為平針繡與盤金繡,選擇銀線刺繡,增強紋樣與服裝整體帶來的視覺效果(圖11)。另外,鶴紋通過機器印花的方式表現出來(圖12)。

圖9 做圓版

圖10 面料堆積在服裝上的表現

圖11 手工刺繡在服裝上的表現

圖12 機器印花在服裝上的表現
3.3 成品效果
本系列設計圍繞中國傳統紋樣展開,所選用的云紋、鶴紋是典型的傳統吉祥紋樣。千百年來,吉祥文化一直是國人對美好生活的熱切表達。作品《承·祥》以現代服飾為載體,通過現代面料堆積、傳統手工刺繡、現代機器印花等工藝手法將傳統紋樣靈活運用在現代服裝設計中(圖13),充分實現了對中國傳統服飾文化的傳承與創新。本系列設計(圖14)將傳統紋樣中流暢的線條、豐富的造型特征和其所蘊含的民族文化通過各種創造手法應用在服飾設計上,不僅是對中國傳統文化的解讀,同時也是對傳統服飾文化的一種繼承。該系列設計作品可以讓中國傳統紋樣在當代得以保存和延續,引發人們對傳統紋樣運用到現代時尚設計中進行打破與再創造的深層思考,進一步詮釋民族文化,增強人們的民族歸屬感和文化認同感。

圖13 采用的工藝手法

圖14 作品《承·祥》成品圖
4 結語
傳統紋樣包含著博大精深的中國傳統文化內涵。在現代服飾設計中運用傳統紋樣,作為設計師應該通過傳統紋樣外化具象的“形”,抓住民族文化抽象的“神”,抽離出傳統紋樣元素的本質內涵,打破對傳統紋樣的具象認識,將傳統元素符號進行解構,使設計的服裝既有時尚感又有文化底蘊[8],這是對中國特色文化服裝設計成長之路的摸索。再設計,需要在不斷創新的同時,把握和突出傳統紋樣的神韻,最終將這種傳統的具有民族特色的元素與現代服裝設計緊密融合,完成這一設計實踐探索既要保留原有的文化內涵,還要賦予其新的時代特征,讓云紋在現代服飾設計中更好地體現現代人的審美價值[9]。以現代設計審美的眼光和手法,將傳統紋樣在造型結構和應用形式上進行一定的創新,通過服裝這一媒介,以單獨紋樣的形式重新組合,表達出傳統紋樣背后的寓意和文化內涵,并以此來尋求傳統文化與現代設計在融合發展過程中的突破,賦予傳統紋樣新的活力和延續力。

