講好例題

彭凌云

例題的作用老師們都知道，無需贅述。例題的講解，老師們幾乎每天都要進行，如何講呢？我想就說說這個事。

一、先做后講

出示例題后，老師不要急于講解，而是先讓學生獨立做一會兒。老師要利用學生做的這段時間，了解學生的思路、亮點、困難處，為后面的講解積累材料。這樣做，老師的講解才能講到學生心坎上，引起學生思維的同步。不顧學生實情的胡亂講解，只能是浪費時間。老師們常常抱怨，不管如何講，講了多少遍，學生面對同樣的問題時還是出錯。盡管原因是復雜的，但肯定與老師講解例題的方式有關。因此，先做后講非常有必要。

例如，教學“兩位數加一位數、整十數”時，老師出示這個例題（如圖所示）后，學生先獨立做幾分鐘。老師巡視，看看學生有哪些做法，然后大家交流。教師再根據全班做、交流的情況，選擇要講的內容。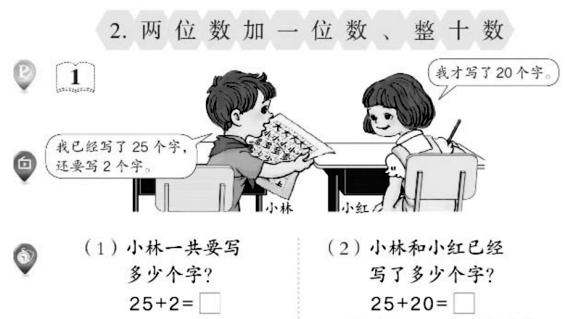

有學生說，25=20+5，2+5=7，因此25+2=27。這種方法就是教材上的，說明是學生很容易想到的方法。

也有學生說，25+2就是從25開始往后再數2，就是27。這里運用的是數數方法。雖然數數方法比較笨，但對數不大的情況還是很管用。這也說明學生對加法概念掌握得很到位。老師應該肯定，同時要指出，如果數比較大，數數就不方便了，希望孩子能夠接受新的算法。

對25+20，學生也會算。25=20+5，20+20=40，40+5=45。因此，25+20=45。

這些算法，如果能出自學生之手，那么，老師再講解將一個數分為整十數與另一個數的和，然后再加，學生記憶就會深刻得多。

二、學會分析

學生對應用題感到難，主要是難在不知從哪兒入手。……