基于AR(m)-QAR-GARCH模型的滬深指數VaR測度研究

奚曉軍 王淼晗 章貴軍

?

基于AR(m)-QAR-GARCH模型的滬深指數VaR測度研究

奚曉軍1王淼晗2章貴軍3

（1．閩南師范大學商學院，福建漳州 363000）（2．上海德勤稅務事務所有限公司北京分所，北京 100738）（3．江西財經大學統計學院，江西南昌 330013）

傳統的GARCH模型在測度我國滬深指數日對數收益率VaR時，由于不能兼顧其尖峰、厚尾、有偏性和自相關性的特征往往效果不佳。針對滬深指數日對數收益率的上述特點，提出利用AR(m)-QAR-GARCH模型測度我國三大股指的VaR。基于Kupiec似然比和DQ檢驗表明：AR(m)-QAR-GARCH模型測度滬深指數VaR預測準確性要好于自相關性不明顯的恒生指數和日經指數；AR(m)-QAR-GARCH模型對滬深指數VaR測度效果要好于幾種沒有考慮自相關性的GARCH模型；對于我國滬深指數收益率自相關性可能存在的階段性特點，AR(m)-QAR-GARCH模型也適合。

VaR；自相關性；GARCH；Kupiec檢驗；DQ檢驗

我國證券交易市場自1990年創立以來，對促進企業融資、繁榮我國金融市場和改善人民收入都起到了非常重要的作用。為了發展和完善我國股票交易市場、降低投資風險，我國政府出臺了一系列與發達國家不同的交易制度。一系列別具一格的交易制度以及我國證券交易市場獨具特色的融資行為和投資行為，都可能造成我國證券指數與發達國家表現不一致的地方。具體可能表現在我國滬深證券指數方面，證券指數是刻畫證券交易市場投資風險的重要指標，成熟的證券市場指數的股指收益率一般不具有自相關性①[1,3]。由于我國證券市場各項制度的改革是逐步出臺的，這可能造成我國證券指數收益率自相關性呈現“此一時，彼一時”的特點。目前，針對這種指數收益率自相關性出現階段性特點，國內外還缺乏對其VaR測度模型的探討。

GARCH類模型能有效地刻畫金融資產收益率波動的聚類特征和異方差現象，逐漸發展成為測度VaR成員中重要的一員。由于傳統的GARCH模型參數估計是在具體的條件分布假定下進行的，當假定的分布不正確時，GARCH模型測度VaR的精確度就會下降[5,9]。為了克服這一缺陷，Engle和Gonzàlez-Rivera提出利用非參數方法可以更好地描述波動率分布特征。結合分位數回歸思想，Koenker和Zhao提出利用不需要對分布進行假定的條件分位數回歸ARCH模型測度波動率情況，并且認為該模型具有更加穩健的估計性質[7]。Xiao和Koenker發展了Q-ARCH模型的思想并提出基于線性GARCH（p，q）的條件分位數自回歸GARCH模型，并提出估計模型參數的兩步估計方法[10]。魏宇的研究表明，GARCH模型可以比較精確地預測我國金融市場VaR[13]。張穎、張富祥對比了遞歸形式的CAViaR和分位數回歸形式的GARCH模型，發現IGARCH-CAViaR模型更適合刻畫相對成熟的美國和日本金融市場風險的演化過程，分位數回歸的GARCH模型對上證綜指和深圳成指描述情況較好[15]。

到目前為止，還沒有基于分位數回歸的GARCH模型在測度VaR時考慮到股市收益率的自相關性問題。我國股市收益率不僅具有尖峰、厚尾和有偏性，而且具有自相關性，因此有必要探討考慮收益率自相關性因素的基于分位數回歸的GARCH模型。鑒于此，本文構建了考慮股市收益率自相關性因素的基于分位數回歸的GARCH模型，然后分析和比較了其在測度我國滬深證券市場收益率VaR時的統計特征。

一、測度模型及檢驗方法

（一）QAR-GARCH模型

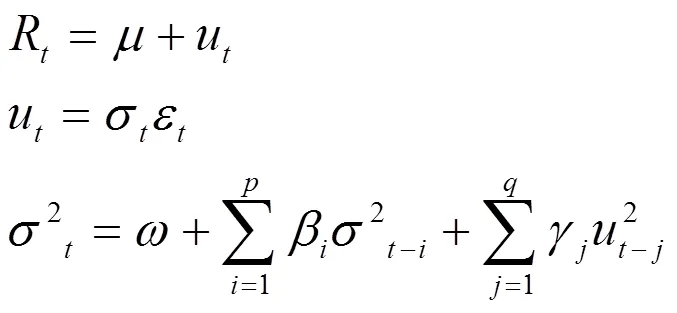
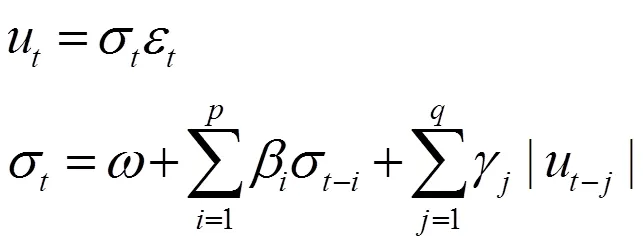
根據VaR定義，有：

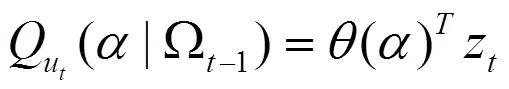
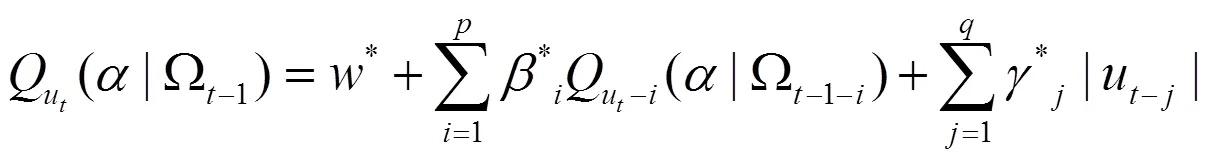
（二）AR(m)-QAR-GARCH模型及估計步驟

本文給出測度VaR時考慮收益率自相關的QAR-GARCH模型，表達式如式（6）所示：

式（6）實際上是由自回歸部分和QAR-GARCH模型兩部分構成，其中自回歸AR(m)部分寫成式（7）的形式：

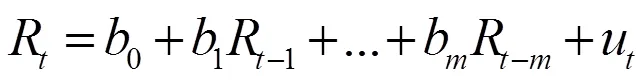
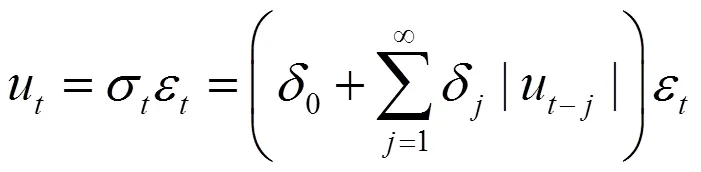
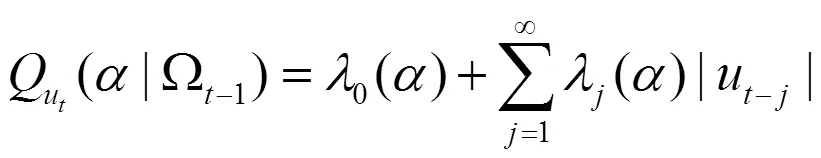
3．采用兩步法對各參數進行估計，得到干擾項的估計值。第一步是估計s階分位數自相關函數。根據干擾項式（8）、（9）構建目標函數（10）：

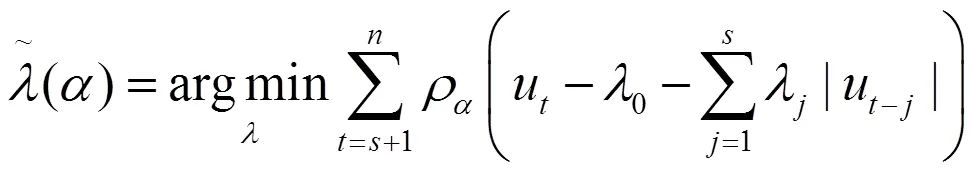
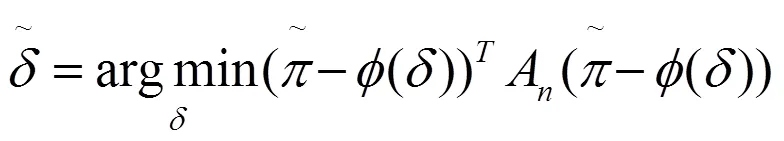
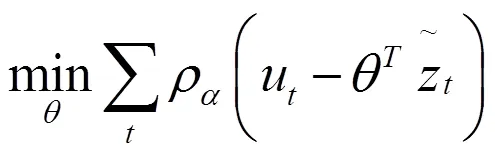
（三）檢驗方法

1．失敗比率

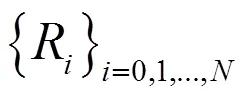
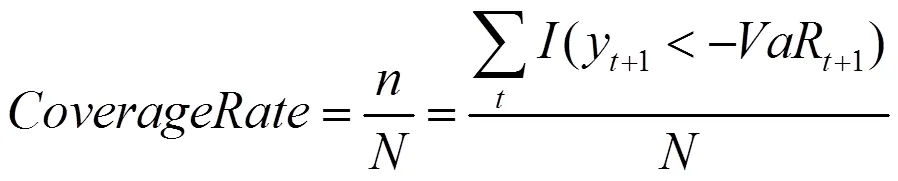
2．Kupeic檢驗

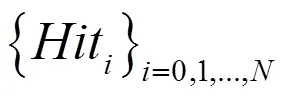
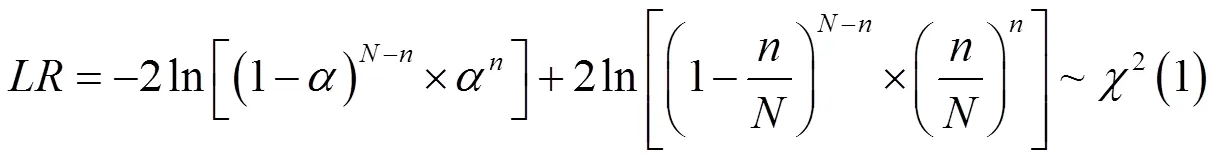
3．DQ檢驗

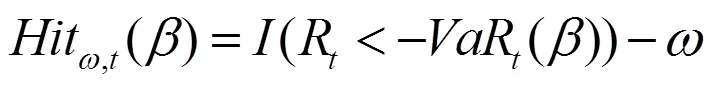
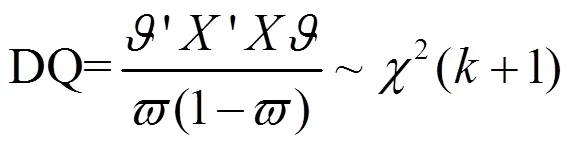
二、樣本數據描述

為了反映我國證券市場收益率波動情況的最新信息，本文選取上證綜指（SSEC）和深證成指（SZSC）2003年1月1日到2014年1月31日的數據，數據來源于DATASTREAM數據庫、谷歌財經和雅虎財經。圖1到圖4（見下頁）分別為各個股指的收益率序列圖，可以看出，上證綜指和深成指股指收益率波動具有較明顯的集聚特征，日經225指數香港恒生收益率集聚特征相對較弱。基于ADF的單位根檢驗結果表明，所有的指數收益率序列均表現平穩。

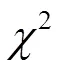
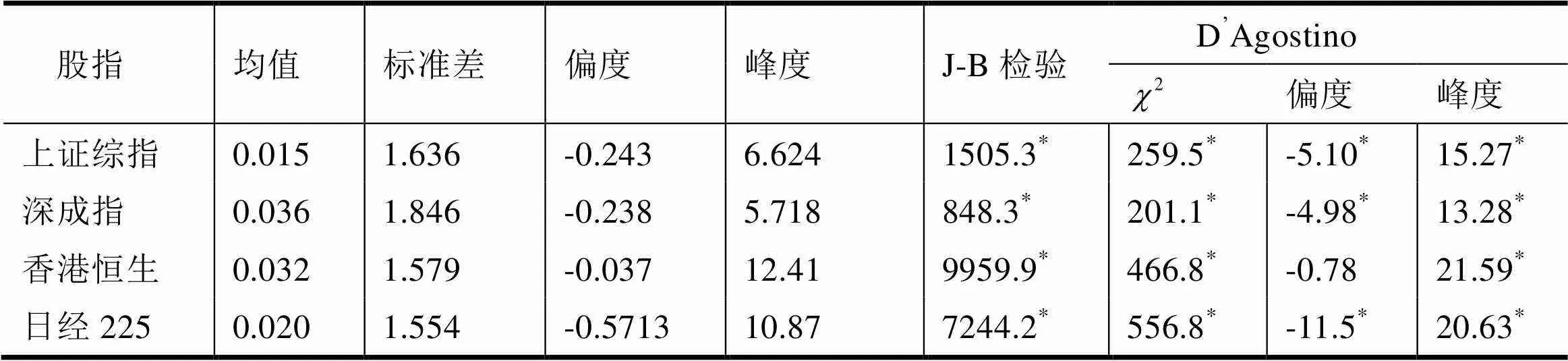
表1 四大股指收益率描述性統計

注：“*”表示相應統計量在1%的顯著水平下拒絕原假設，“**”，表示相應統計量在5%的顯著水平下拒絕原假設，“***”表示相應統計量在10%的顯著水平下拒絕原假設

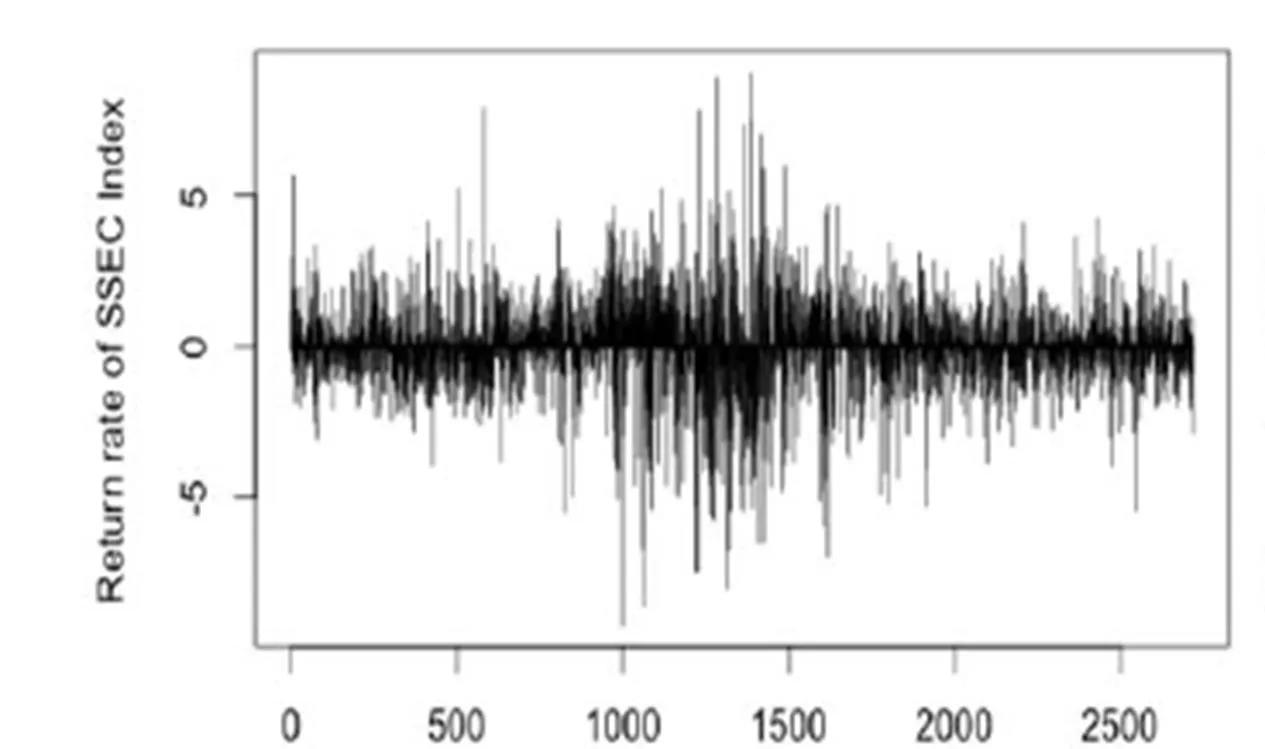
圖1 上證綜指收益率序列

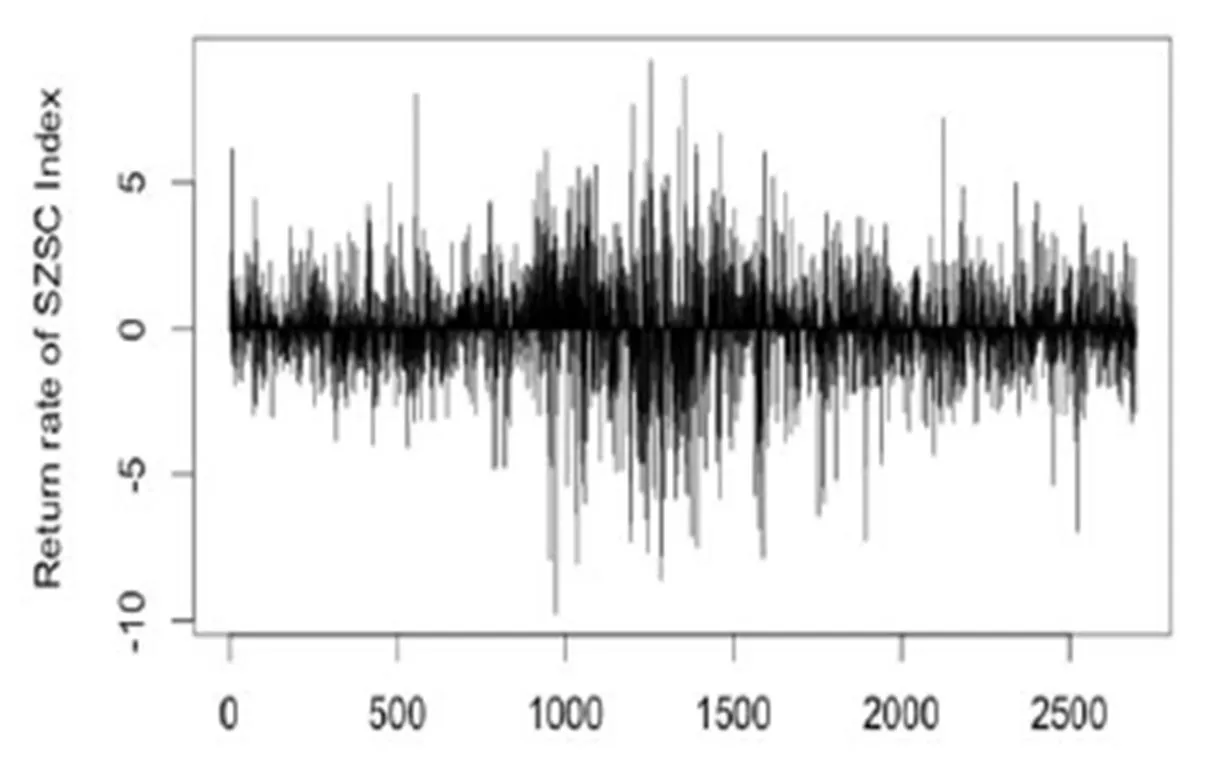
圖2 深證成指收益率序列

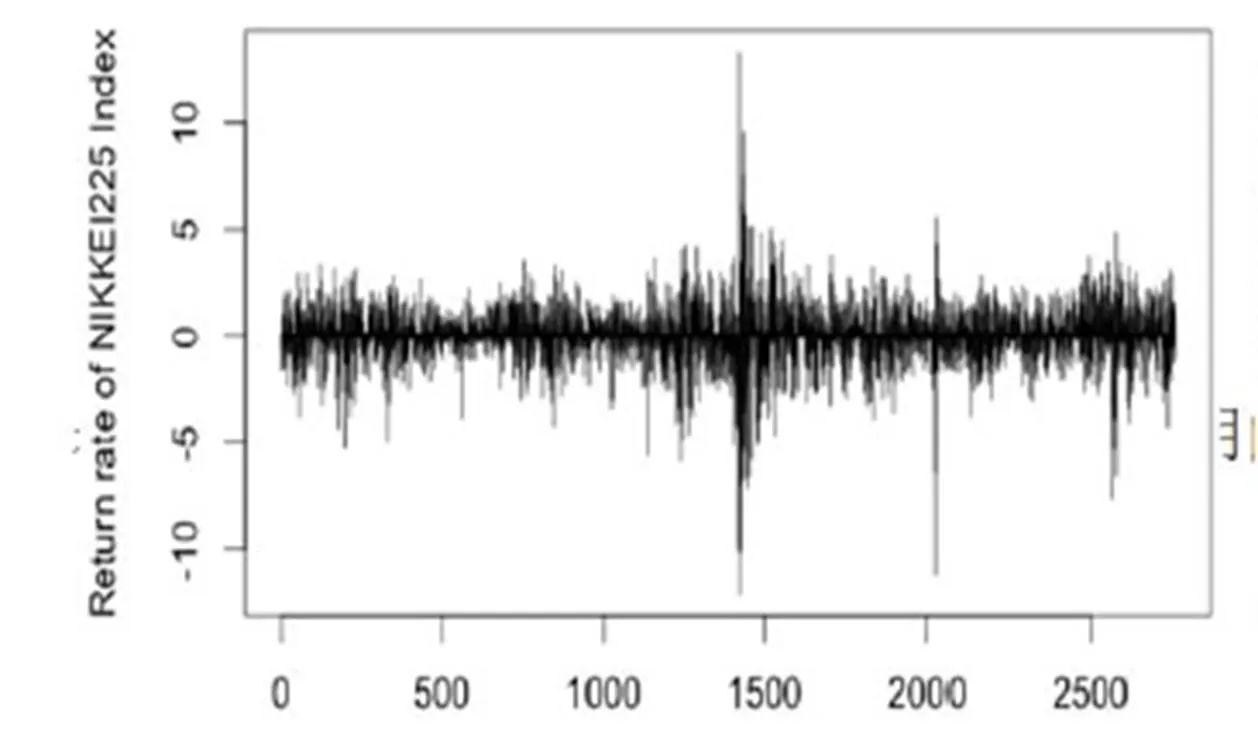
圖3 日經225指數收益率序列

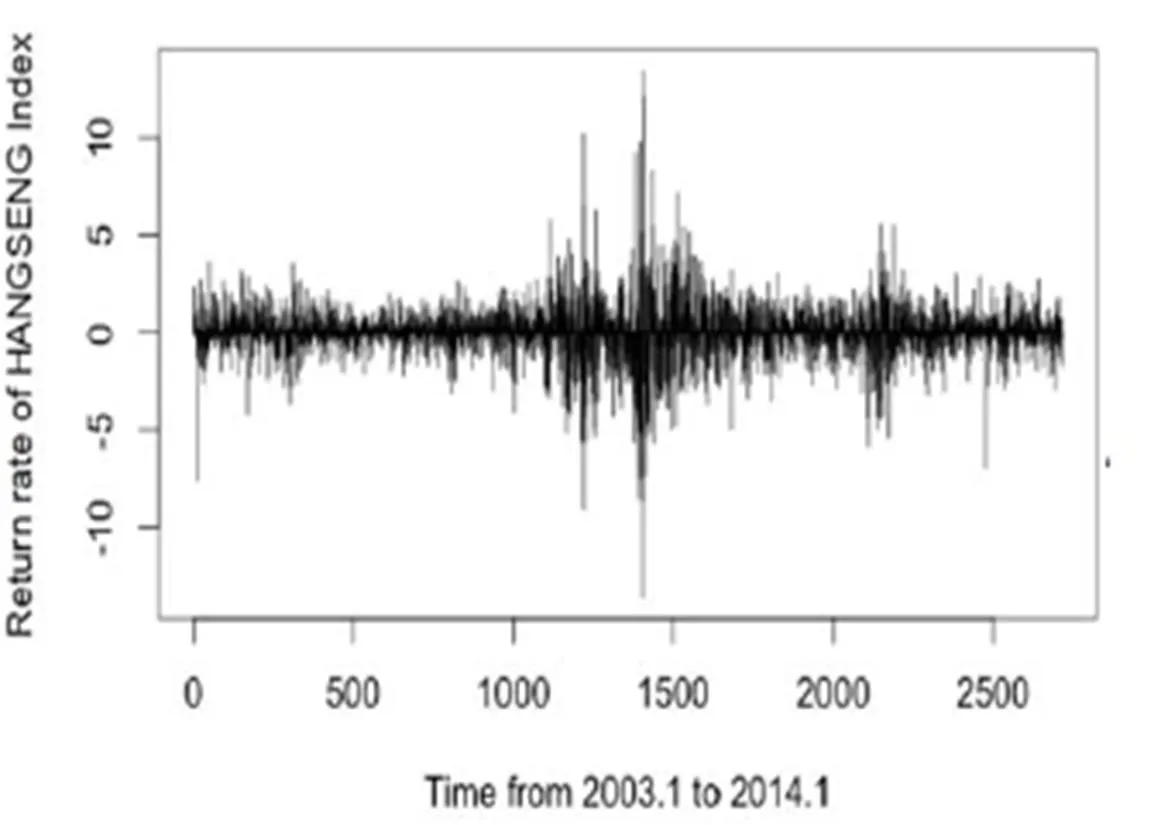
圖4 恒生指數收益率序列

表2為我國三大股指及日經225指樣本期內股指對數收益率數據自相關性檢驗結果。基于低階自相關性檢驗的統計量表明：上證綜指和深證成指收益率存在明顯的高于三階的自相關性，香港恒生存在微弱4階自相關性及日經225收益率不存在明顯的自相關性。自相關性檢驗結果同時說明測度我國滬深指數收益率時應考慮高階自相關性，測度相對比較成熟證券市場股指（如香港恒生和日經225）收益率時不必考慮自相關性。

表2 四大股指收益率自相關性檢驗

三、模型測度結果與比較

根據各大股指數據、VaR測度公式以及Kupeic統計量和DQ統計量測度公式，本文將各種計算結果整理得到表3和表4所示數據。

（一）AR(m)-QAR-GARCH對四大股指收益率VaR測度結果比較

表3數據為AR(m)-QAR-GARCH模型對四大股指收益率VaR測度結果。從表3測度結果不難看出，AR(m)-QAR-GARCH模型對我國上證綜指的風險預測準確性相對比較高，檢驗結果反映訓練集及測試集中VaR都非常接近真實水平。同時，測試集上的計算結果表明， AR(4)-QAR-GARCH模型在1%和5%的分位點上的Kupiec統計量對應的概率值都非常接近1，表明其對上證指數VaR的預測精確程度明顯高于對其它指數VaR的預測，這一結論恰好與表2中反映的上證指數收益率存在較強的4階自相關性一致。

對于深圳成指VaR測度而言，AR(3)-QAR-GARCH和AR(4)-QAR-GARCH模型樣本集內測度結果擬合度非常高，計算得到的失敗比率都十分接近0.01和0.05，并且Kupiec統計量對應的概率值接近于1；在測試集上，兩個模型VaR估計結果的Kupeic統計量對應的概率值略小于訓練集，但均不能拒絕模型有效的原假設，雖然其對測試集數據VaR的估計能力相對較弱，但其預測準確性也不差，Kupiec統計量對應的概率值至少也達到了0.7。

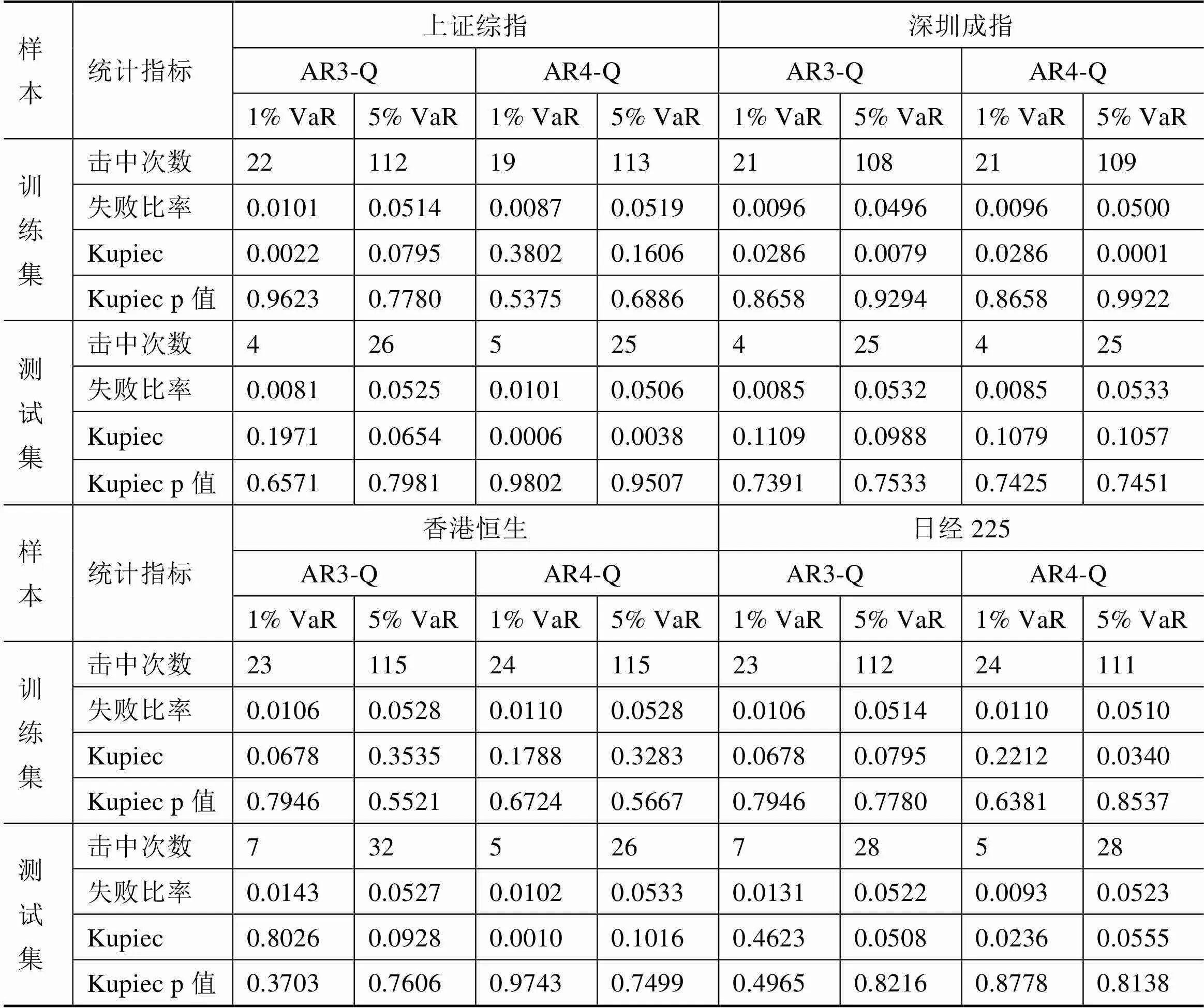
表3 AR(m)-QAR-GARCH模型對四大股指VaR測試結果比較

注：表3中AR3-Q為3階自回歸分位數GARCH模型，表3中AR4-Q為4階自回歸分位數GARCH模型；由于空頭頭寸的計算結果幾乎與多頭一致，本文僅列舉多頭情況

由表3還可以看出，無論是訓練集還是測試集中，AR(4)-QAR-GARCH模型在1%水平和5%水平上對恒生指數VaR的測度效果相對較好，測度結果都十分逼近真實風險值，AR(3)-QAR-GARCH模型測度效果比AR(4)-QAR-GARCH稍差一點，這也印證了表2中恒生指數收益率4階自相關性強于3階自相關性的檢驗結論。AR(m)-QAR-GARCH模型在1%水平和5%水平上對日經225指數VaR的預測結果也不差，雖然Kupeic統計量對應的概率沒有大于0.9的高概率值，但至少也達到了0.5。此外，比較分析發現，在1%分位水平上，AR(m)-QAR-GARCH模型對恒生指數VaR預測的性明顯高于日經225指數，可能是因為恒生指數收益率存在微弱的4階自相關性的緣故。

此外，無論是訓練集還是測試集中，由AR(3)-QAR-GARCH和AR(4)-QAR-GARCH模型測度的四大指數的VaR的DQ檢驗統計量均不能拒絕原假設，檢驗結果見表4。此外，表3結果表明，所有Kupeic統計量對應的概率值均不能拒絕測度模型VaR測度結果。這說明對于即使不存在自相關性的香港恒生指數和日經225指數，利用AR-QAR-GARCH模型測度的VaR也不會表現太差。

（二）不同模型VaR測度結果比較

表4反映了QAR-GARCH和AR(m)-QAR-GARCH模型與其它常見的GARCH模型VaR測度結果統計檢驗數據。鑒于表1對數據檢驗表明四大股指收益率均具有尖峰、偏態和厚尾的特征，所以均采用基于Skewed-t（有偏的學生分布）分布的GARCH用于比較，主要有EGARCH、IGARCH和GJRGARCH。通過對QAR-GARCH和AR(m)-QAR-GARCH模型與其它三種GARCH模型VaR測度的統計檢驗檢驗結果表明3個方面的內容。

1．AR(m)-QAR-GARCH模型對滬深指數VaR測度表現相對較好。無論是Kupiec統計量對應的概率值，還是DQ統計量概率結果均超過0.7，相對于其它模型而言AR(m)-QAR-GARCH模型對我國滬深指數VaR測度效果良好。從表4檢驗結果同時可以看出，雖然QAR-GARCH、EGARCH、IGARCH和GJRGARCH模型測度效果略遜于AR(m)-QAR-GARCH模型，但總體表現并不差，可能由于其都考慮到了滬深指數的尖峰、厚尾和有偏的特征。因此，有理由認為AR(m)-QAR-GARCH模型對滬深指數VaR測度效果較好的原因是考慮了滬深指數收益率的自相關性問題。

2．AR(m)-QAR-GARCH模型對恒生指數和日經指數VaR測度并無明顯優勢。表4檢驗結果同時表明，雖然AR(m)-QAR-GARCH對滬深指數VaR測度表現相對較好，但對恒生指數和日經指數VaR測度并無明顯優勢。對恒生指數的VaR測度中，在1%分位點上，AR(m)-QAR-GARCH和GJR效果相對較好，檢驗統計量對應的概率值都達到了0.6，AR(4)-QAR-GARCH模型準確率稍高于GJR；在5%分位點上，QAR-GARCH、AR(m)-QAR-GARCH、IGARCH和GJR表現效果均不差，此時GJR模型預測準確率稍高于AR(4)-QAR-GARCH模型。在對對日經指數的VaR測度中，QAR-GARCH和GJR表現效果相對較好。顯然，上述分析表明，AR(m)-QAR-GARCH之所以對恒生指數和日經指數VaR測度無優勢，可能是二者不存在明顯自相關性的原因。同時不難看出，對于測度指數收益率不存在自相關性的VaR而言，利用考慮自相關性的模型可能并不是一件壞事，雖然無助于顯著改善測度效果，但也并沒有顯著降低測度效果。所以，對于滬深指數自相關性可能存在“此一時，彼一時”的階段性特點，考慮自相關性的AR(m)-QAR-GARCH模型測度其VaR相對比較可靠。

3．基于分位數回歸的GARCH模型好于基于Skewed-t參數分布的GARCH模型。針對文中的四大股指而言，從Kupiec統計量和DQ統計量對應的概率值是否小于顯著水平上來看，基于分位數位數回歸的GARCH模型好于Skewed-t參數分布的GARCH的模型。一個可能是原因是基于分位數回歸的非參數不受股指收益率分布的影響，而基于參數分布的GARCH模型可能會降低估計效果[11-16]。具體而言，對于滬深指數的受益率VaR測度結果，AR(4)-QAR-GARCH模型效果最好，IGARCH模型效果相對較差；對于恒生指數和日經指數的VaR測度結果，除EGARCH模型表現較差外，參數方法和非參數方法差別不明顯。

表4 不同GARCH模型VaR測度檢驗結果比較

注：表4中計算結果均根據測試集中數據計算得到，其中QGAR為QAR-GARCH模型，EGAR為E-GARCH模型，IGAR為IGARCH模型，GARCH模型、IGARCH模型及GJR模型均為基于Skewed-t的計算結果

四、結 論

本文構建了考慮自相關性的分位數回歸GARCH模型，即AR(m)-QAR-GARCH模型，分別在訓練集和測試集中的不同分位數水平上根據測度的Kupiec統計量和DQ統計量比較了AR(m)-QAR-GARCH模型對我國滬深指數VaR測度的準確性。最后，在測試集中的不同分位數水平上比較了AR(m)-QAR-GARCH模型和其它常見的GARCH模型對我國滬深指數VaR、香港恒生指數和日經225指數VaR測度效果。具體而言，得到如下三個方面的結論：

1. AR(m)-QAR-GARCH模型在測度滬深指數VaR時效果要好于自相關性不明顯的恒生指數和日經225指數。通過比較AR(m)-QAR-GARCH模型對四大股指VaR測度的準確性，我們發現，無論在訓練集中，還是測試集中AR(m)-QAR-GARCH模型對我國滬深指數VaR測度準確性均好于恒生指數和日經225指數。這說明由于我國滬深指數收益率具有明顯自相關性，AR(m)-QAR-GARCH模型對其VaR測度的準確性要高于不具有明顯自相關性的恒生指數和日經225指數。

2. AR(m)-QAR-GARCH模型對滬深指數VaR測度效果要好于幾種沒有考慮自相關性的GARCH模型。通過比較AR(m)-QAR-GARCH模型和QAR-GARCH、EGARCH、IGARCH和GJRGARCH模型對我國滬深指數VaR恒生指數和日經225指數VaR測度效果發現：對于存在明顯自相關性的滬深指數而言，AR(m)-QAR-GARCH模型測度效果優于其它GARCH類模型；對于存在明顯自相關性的香港恒生指數和日經225指數，AR(m)-QAR-GARCH模型與其它GARCH類模型，特別是GJR模型相比，并無明顯優勢。

3. AR(m)-QAR-GARCH模型適合于測度指數自相關性存在階段性特點的VaR。雖然考慮了自相關性的AR(m)-QAR-GARCH模型對不存在自相關性的指數而言并無明顯的比較優勢，但相對于其它GARCH模型而言，無論是預測準確性方面，還是測度效果方面都表現良好。該模型也適用于測度即使沒有明顯自相關性的恒生指數和日經指數。所以，針對我國滬深指數自相關性可能存在“此一時，彼一時”的階段性特點，考慮自相關性的AR(m)-QAR-GARCH模型測度其VaR相對比較可靠。

[1] A W Lo. Long-term memory in stock market prices [J]．Econometrica, 1991（9）：1279-1313．

[2] D B Nelson．Conditional heteroscedasticity in asset returns: a new approach [J]． Econometrica,1991（2）：347-370．

[3] E F Fama．Efficient capital markets: П [J]．The Journal of Finance, 1991（12）：1579-1622．

[4] R F Engle．Dynamic conditional correlation-A simple class of multivariate GARCH models[J]．Journal of Business and Economic Statistics,2002,working paper．

[5] R F Engle，G Gonzàlez-Rivera．Semiparametric ARCH Models [J]．Journal of Business & Economic Statistics,1991（9）：345-359．

[6] R F．Engle，S Manganelli．CAViaR: Conditional Autoregressive Value at Risk by Regression Quantiles [J]．Journal of Business and Economic Statistics, American Statistical Association, 2004（10）：367-381．

[7] R Koenker，Q Zhao．Conditional Quantile Estimation and Inference for Arch Models [J]．Econometric Theory，Cambridge University Press，1996 (5)：793-813．

[8] R T Baillie,T Bollerslev,H O Mikelsen．Fractional integrated generalized autoregressive conditional heteroscedasticity [J]．Journal of Econometrics，1996（9）: 3-30．

[9] Y Sun, T Stengos．Semiparametric efficient adaptive estimation of asymmetric GARCH models [J]．Journal of Econometics,2006（1）：373-386．

[10] Z J Xiao,R Koenker．Conditional Quantile Estimation for GARCH Models [J]．Boston College Working Papers in Economics 725，Boston College Department of Economics，2009．

[11] 方立兵，郭炳伸，曾勇．GARCH族模型的預測能力比較：一種半參數方法[J]．數量經濟技術經濟研究，2010（4）：148-160．

[12] 龔銳，陳仲常，楊棟銳．GARCH族模型計算中國股市在險價值（VaR）風險的研究比較評述[J]．數量經濟技術經濟研究，2005（6）：67-82．

[13] 魏宇．有偏胖尾分布下的金融市場風險測度方法 [J]．系統管理學報，2007（6）：243-250．

[14] 徐煒，黃炎龍．GARCH模型與VaR的度量研究 [J]．數量經濟技術經濟研究，2008（1）：120-132．

[15] 張穎，張富祥．分位數回歸的金融風險度量理論及實證[J]．數量經濟技術經濟研究，2012（4）：96-109．

[16] 趙樹然，任培明，趙昕．基于CARR-EVT整體方法的動態日VaRhe CVaR模型研究[J]．數量經濟技術經濟研究，2012（11）：130-148．

（責任編輯：鄭宗榮）

① Lo（1991）和Fama（1991）認為成熟的證券市場一般滿足有效性市場假說，或者至少滿足弱有效性市場假說。

②更詳細的描述，可以參看徐金菊，許啟發（2013）的文獻。

VaR Measurement of Shanghai and Shenzhen Composite Index Based on AR(m)-QAR-GARCH Model

XI Xiaojun1WANG Miaohan2ZHANG Guijun3

Traditional GARCH-based model usually performs not so good when measuring VaR about log return rate of Shanghai and Shenzhen composite index without consideration of their property of leptokurtic, skewed and fat-tailed distribution and autocorrelation at the same time. This study proposes AR(m)-QAR-GARCH to measure three security exchange indices in our country with consideration of their distribution property and autocorrelation. Three main results of this study are attained by the use of Kupiec likelihood ratio test and DQ test. Firstly, we find that the model proposed by this study predicts more exactly than in the use of measuring VaR of Shanghai composite index and Shenzhen composite index than it has been used of HIS and Nikkei 225 index. Secondly, the model performs better than other GARCH-based model ignorance of volatility autocorrelation when measuring VaR of Shanghai composite and Shenzhen composite index. Thirdly, we also find that AR(m)-QAR-GARCH model also has good performance for measuring the VaR of Shanghai composite and Shenzhen composite index when the autocorrelation of them appear in a phase and disappear in another phase.

VaR; autocorrelation; GARCH; Kupiec test; DQ test

F222.3

A

1009-8135（2018）04-0042-12

奚曉軍（1978—），男，吉林九臺人，閩南師范大學商學院講師，主要研究金融計量經濟學。王淼晗（1989—），女，內蒙古包頭人，上海德勤稅務事務所有限公司北京分所員工。章貴軍（1978—），男，湖北監利人，江西財經大學統計學院、江西財經大學應用統計研究中心、江西財經大學博士后流動站講師，主要研究數量經濟學。

國家社會科學基金一般項目“精準貧困識別和扶貧瞄準的統計測度研究”（16BTJ011）；福建省教育廳社會科學研究項目“福建省財產保險公司運行機制穩定性研究”（JAS160315）。