基于Memetic混合算法的橋區復雜水域船舶航路規劃

楊帆， 王健宇,1b， 楊柯， 徐言民

(1. 武漢理工大學 a. 航運學院; b. 內河航運技術湖北省重點實驗室, 武漢 430063;2. 安康市漢濱區交通運輸局， 陜西 安康 725000)

0 引 言

近年來，自動化技術被應用到交通領域，無人機、無人艇、無人駕駛汽車等技術得到了飛速發展[1-2]。我國長江深水航道工程的實施和沿江港口的大規模建設，使交通流密度增大，局部通航條件更加復雜。目前船舶在群橋水域[3-4]航行時，仍然采用傳統的手動操舵，而以往船撞橋事故主要是由人的失誤引起的，因此，實現船舶在多障礙物復雜水域的自主航行，既是減少船撞橋事故的有效手段，又是急需攻克的技術難題。

船舶航路規劃是實現船舶自主航行的重要前提。船舶航路規劃問題屬于多維非線性優化問題。如果考慮通航水域的動態障礙物，則船舶航路規劃問題屬于非線性時變函數優化問題[5]，這對航路規劃求解算法的收斂性、時效性要求很高，傳統算法難以適用。現有群智能算法具有自適應、自組織和自學習的特點，能夠解決傳統算法難以解決的非線性復雜問題，在航路規劃方面具有很好的應用前景[6-7]，但運用該算法求解得到的多維非線性函數優化問題的解均為近似解，仍然有進一步優化的空間。

本文通過分析以長江武漢段群橋水域為典型代表的復雜水域通航特征，建立復雜水域通航環境模型，然后進一步建立復雜水域航路規劃數學模型。為提高算法求解精度和求解速度，為動態環境航路規劃研究奠定基礎，結合遺傳算法的全局搜索能力和模擬退火算法的局部搜索能力，設計了Memetic混合算法，對所建立的模型進行求解，并對規劃航路進行優化處理。

1 航路規劃模型

1.1 復雜水域通航環境特征簡要分析

目前，學術界對于復雜水域并沒有明確定義。一般來講，復雜水域具有較為復雜的水文、交通流、通航條件、船舶狀況等。本文將以群橋水域為代表的、存在近距離的多個障礙物的水域視為復雜水域。

通常情況下，橋區復雜水域的橋墩、淺點、沉船等障礙物間距小，障礙物分布無規律[8]；障礙物的挑流作用使得復雜水域的水流更加復雜；考慮安全水深因素，復雜水域內供船舶航行的水域往往被限制；復雜水域交通流復雜，船舶操縱難度大，非常容易發生碰撞事故。

1.2 橋區復雜水域通航環境建模

如果不考慮動態障礙物影響，則以橋區水域為代表的復雜水域最主要的障礙物是橋墩。本文假定研究水域障礙物為圓形。考慮障礙物的挑流作用和安全裕度，適當地擴大障礙物尺寸，在水域一定范圍內隨機生成大小不同的障礙物，見圖1。

為使規劃結果更加直觀，圖1中船舶被視為質點，障礙物的半徑被等比例擴展，這樣便可保證船舶與障礙物之間的距離仍符合要求。圖1橫、縱坐標中的L為船長。

包括起點和終點的所有黑點按順序連接成的折線可表示搜索空間中的某一條路徑，路徑點與障礙物間的距離是判斷航路危險性的主要依據。為便于在選取最優路徑時進行路徑長度計算，需要建立通航環境坐標系，將坐標系按如下關系進行轉換：XOY為原坐標系，新坐標系為X′O′Y′，路徑點在原坐標系和新坐標系中的坐標分別為(x,y)和(x′,y′)，在原坐標系中起點和終點的坐標分別為(xs,ys)和(xt,yt),θ為兩個坐標系橫軸的夾角。坐標轉換關系見圖2。

圖2 坐標轉換關系

路徑點坐標在兩個坐標系中的轉化公式如下：

(1)

1.3 橋區復雜水域航路規劃數學模型

船舶航行最重要的原則是安全、經濟、高效，因此最優的航路規劃就是找到一條從起點(xs,ys)到終點(xt,yt)的與障礙物不相交且長度最短的路徑。本文先求出最短的路徑，再對其進行實用化處理。按照文獻[9]，航路規劃數學模型為

(2)

式中：L為航路總長；J為航路跟蹤代價；J1為障礙物威脅代價；J2為航路長度代價；wt表示航路上各點的威脅代價；wl表示每條邊的長度代價；k為不同航路跟蹤代價所占的比例，設定路徑規劃中障礙物威脅代價與路徑長度代價同等重要，故本文k取0.5。

選取起點與終點之間線段的一部分(起始于M，終止于N)，分成10等份，在每個等分點(共9個等分點)處作MN的垂線。在每條垂線上各選擇一個點，將這些點按從M到N的順序連成一條航路LMN。當船舶沿著航路LMN航行時，威脅源(障礙物)個數為n，則總威脅代價為

(3)

為方便計算，在線段MN上取5個點(見圖3)，按下式計算航路的障礙物威脅代價：

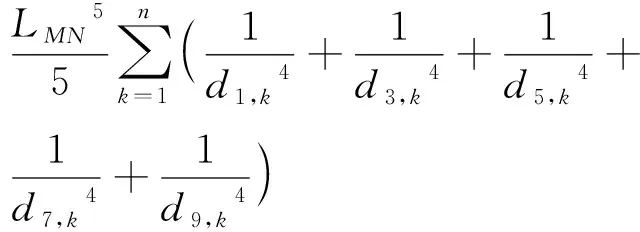
(4)

d1,k、d3,k、d5,k、d7,k、d9,k分別表示MN上的第1、3、5、7、9個等分點與第k個障礙物中心的距離。

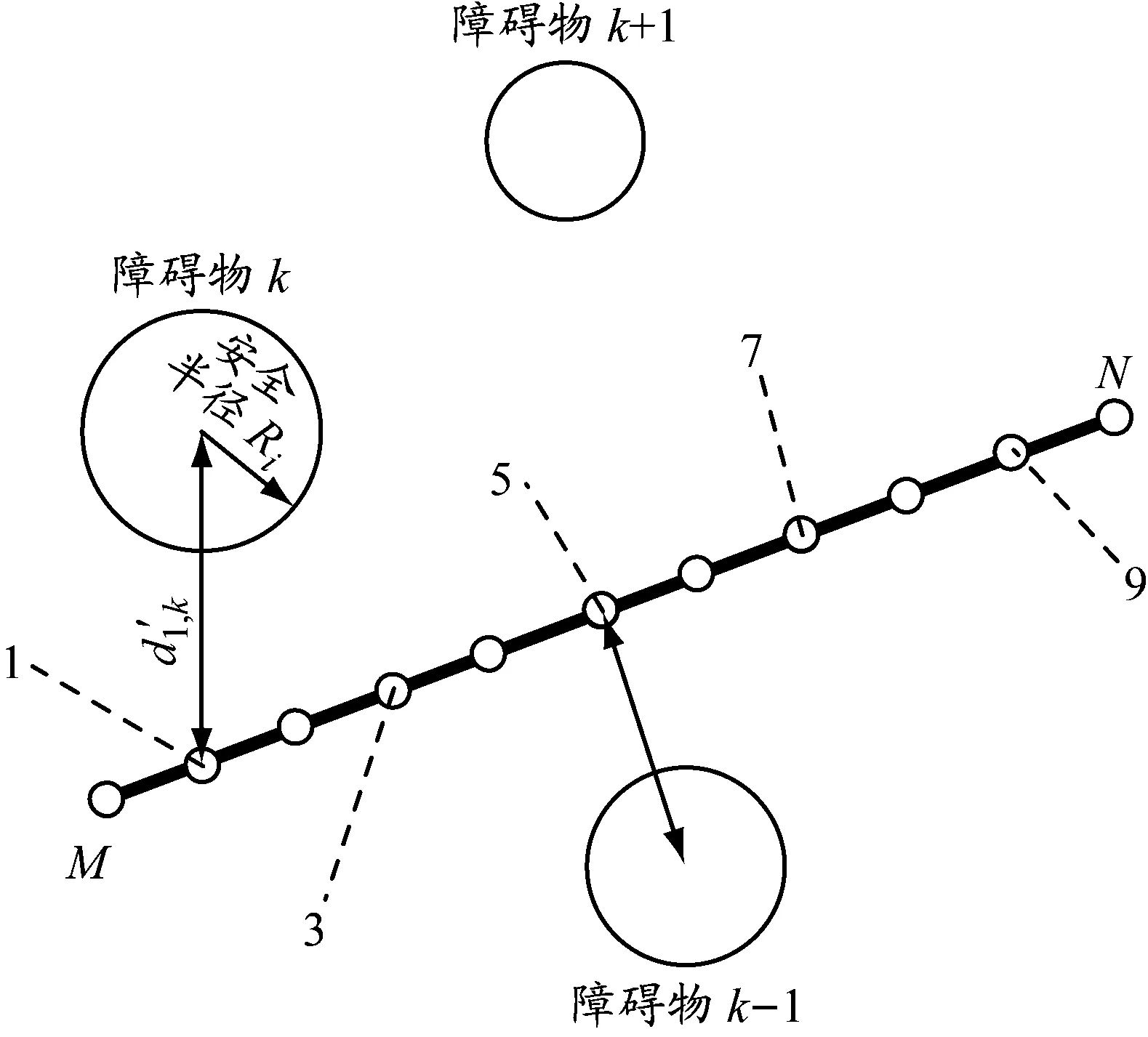
圖3 障礙物威脅代價示意圖

2 Memetic算法設計

2.1 Memetic算法概述

Pablo Moscato于1989年首次提出Memetic算法的概念[10]。Memetic一詞由meme而來，可理解為“文化基因”，因此Memetic算法可稱為文化基因算法[11]。Memetic算法最初的主要思想是在遺傳算法每次迭代后對所有種群進行一次局部搜索，它實際上是一種混合算法。算法用局部啟發式搜索來模擬由大量專業知識支撐的變異過程，使得遺傳算法的變異得到有效的支撐，從而使算法在某些領域的搜索速度和計算精度有了極大提高。

2.2 Memetic算法設計

實際上，Memetic算法只是提供了一個算法框架，是全局搜索策略和局部搜索策略的有機結合。本文全局搜索策略采用遺傳算法，局部搜索策略采用模擬退火算法。有關遺傳算法和模擬退火算法的相關研究較多，這里不贅述。

通過代碼設計，種群在每次更新后都會在其個體領域進行局部搜索，從而使得算法能夠快速收斂于最優解。

遺傳算法中參數設置的相關研究已有很多，本文選擇較為常用的參數設置。降溫過程的快慢會影響模擬退火算法的全局搜索能力與局部搜索能力的平衡[12]。在計算機實現中，如果降溫速度慢，則會得到令人滿意的解，但如果降溫速度太慢，則其相較于其他簡單的搜索算法不具有明顯優勢[13]；如果降溫速度快，則該算法更容易求得局部最優解。初始溫度高低也會影響模擬退火算法運行，較高的初始溫度更容易求得全局最優解，但會大大增加算法復雜度，影響算法的求解時間。本文的算法更關注模擬退火算法的局部搜索能力，因此本文設置的初始溫度較低，降溫速度較快。

3 航路規劃

根據上述算法，本文給定障礙物坐標分別為(21L，20L)，(26L，55L)，(40L，10L)，(55L，5L)，(55L，30L)，(55L，45L)，(55L，75L)，(73.3L，53.5L),(90.9L， 23.9L)。為增加航路規劃難度，將航路規劃的起點和終點設置在障礙物分布較為集中的連線上，起點坐標設置為(5L，5L)，終點坐標設置為(110L，70L)。分別使用遺傳算法、模擬退火算法和Memetic混合算法進行航路規劃。Memetic混合算法迭代次數設置為300，其中模擬退火模塊內部迭代次數設置為100。求解結果見圖4和5。

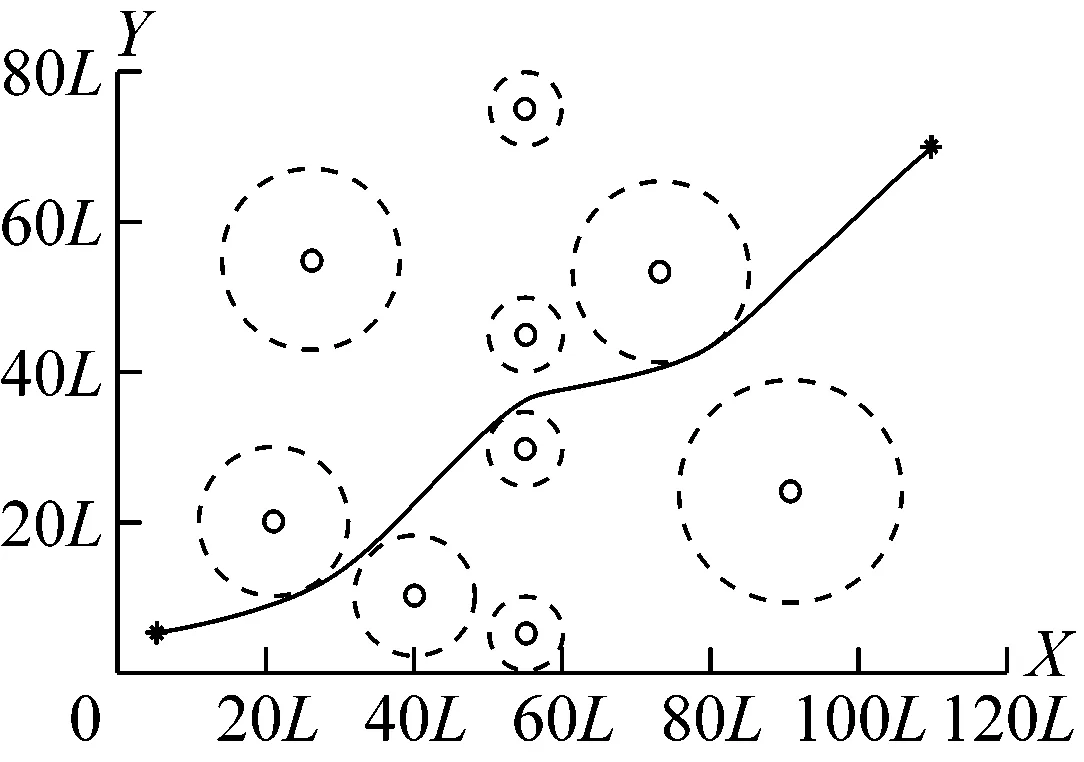
a)Memetic混合算法

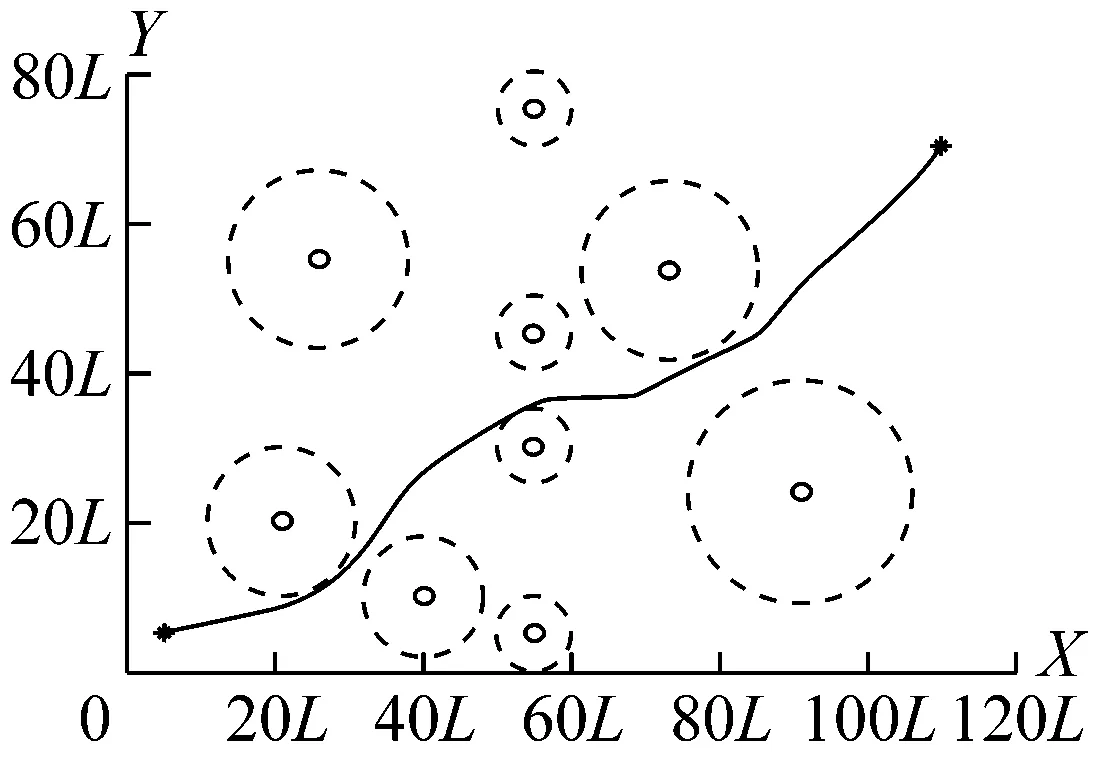
b)遺傳算法

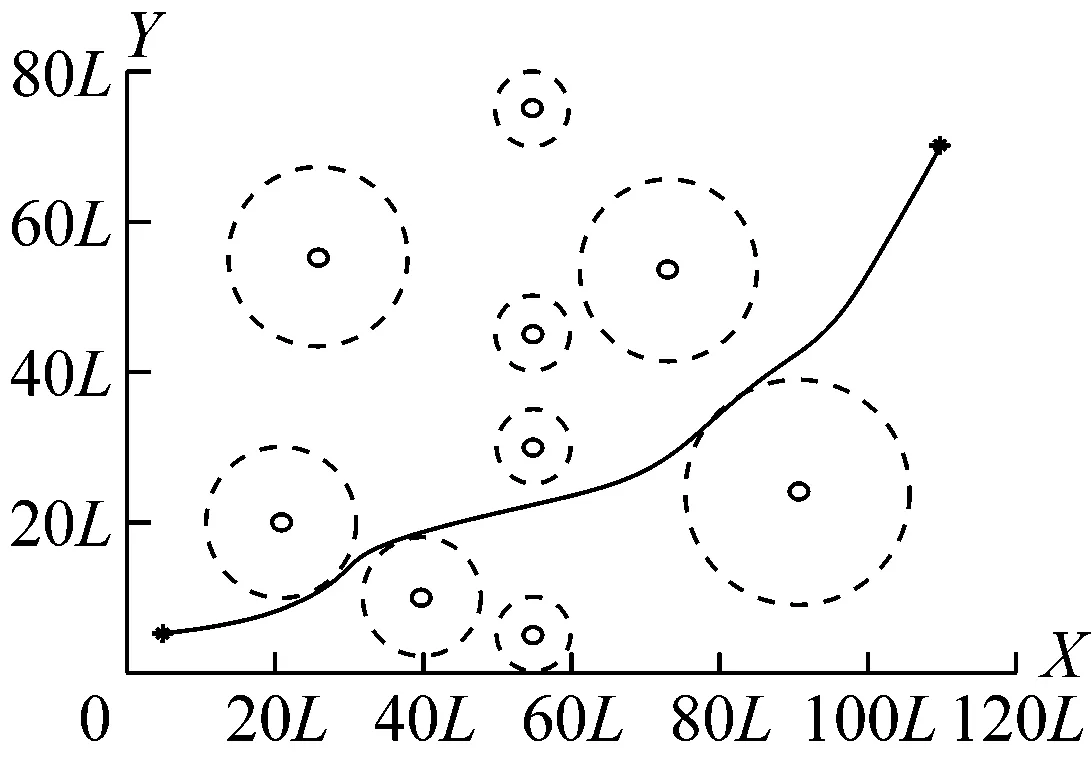
c)模擬退火算法圖4 3種算法航路規劃示意圖

a)Memetic混合算法

b)遺傳算法

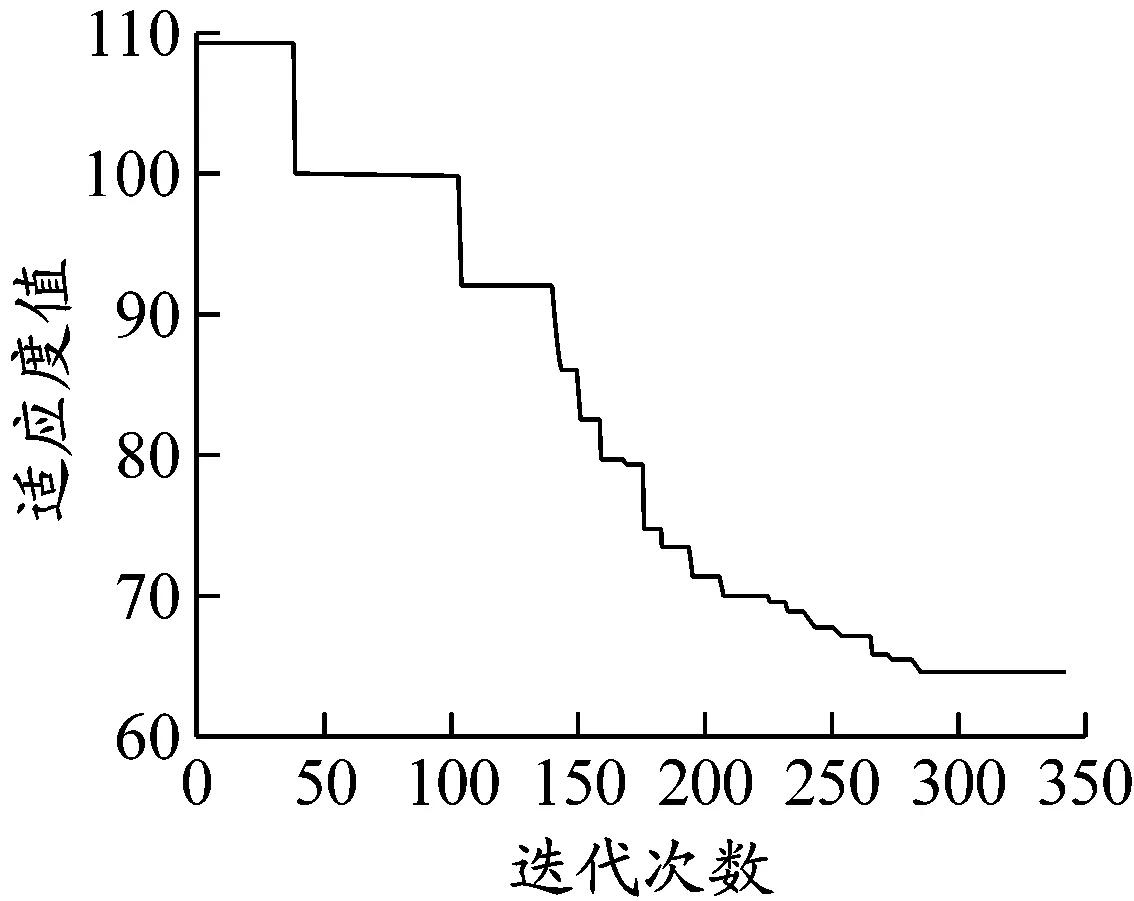
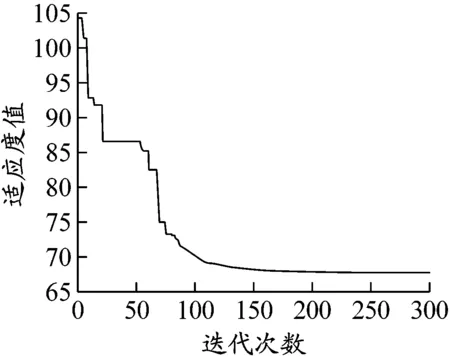
c)模擬退火算法圖5 3種算法迭代曲線示意圖

由圖5可以看出，Memetic混合算法能更快地求出最優解，算法大約在迭代次數為150時穩定收斂。

Memetic混合算法既結合了遺傳算法的全局搜索能力，又在每次迭代過程中利用了模擬退火算法的局部搜索能力，使得算法收斂速度和求解精度有了極大的提高。

4 規劃航路優化

針對D維優化問題，本文設計的算法能夠尋找出D維最優解。對應本文所建立的規劃模型，規劃航路為D維向量加起始點的一組向量。為提高求解精度，常常將D取得比較大，最終求解的航路規劃問題維數較多，得到的航路呈現出曲線或者有較多段線段的形態。另外，由于本文設計的算法求解的是目標函數的近似最優解，從規劃結果圖上可以直接看到規劃航路在終點附近還存在一定的彎曲度，仍然有優化的空間。

利用所建立的模型，所選取的航路為端點(M和N)與9個節點所組成的10條線段。一種很簡單的改進思想是：所求得的航路是一個近似最優解，在其附近的其他航路應該也是相對較優的。因此，可考慮在已經規劃出來的10條線段中，以M點為第1個點，如果相鄰兩條線段的傾斜角差的絕對值小于一定的閾值，則可去掉相鄰兩條線段中間的點，兩條線段轉化為一條線段，否則這部分航路保持不變。依次進行以上操作，直到算法歷經所有的11個點為止。如圖6所示，假設第1個點為點k，由點k與k+1、點k+1與k+2，分別確定線段lk,k+1和lk+1,k+2。因為lk,k+1與lk+1,k+2的傾斜角差小于給定閾值，所以挖去點k+1，由新的線段l1取代原來的兩條線段lk,k+1和lk+1,k+2，這樣就達到了減少轉向點的目的。接著對線段l1與線段lk+2,k+3的傾斜角差做上述比較，因為l1與lk+2,k+3的傾斜角差值仍小于給定閾值，所以可用新的線段l2取代l1和lk+2,k+3兩條線段。

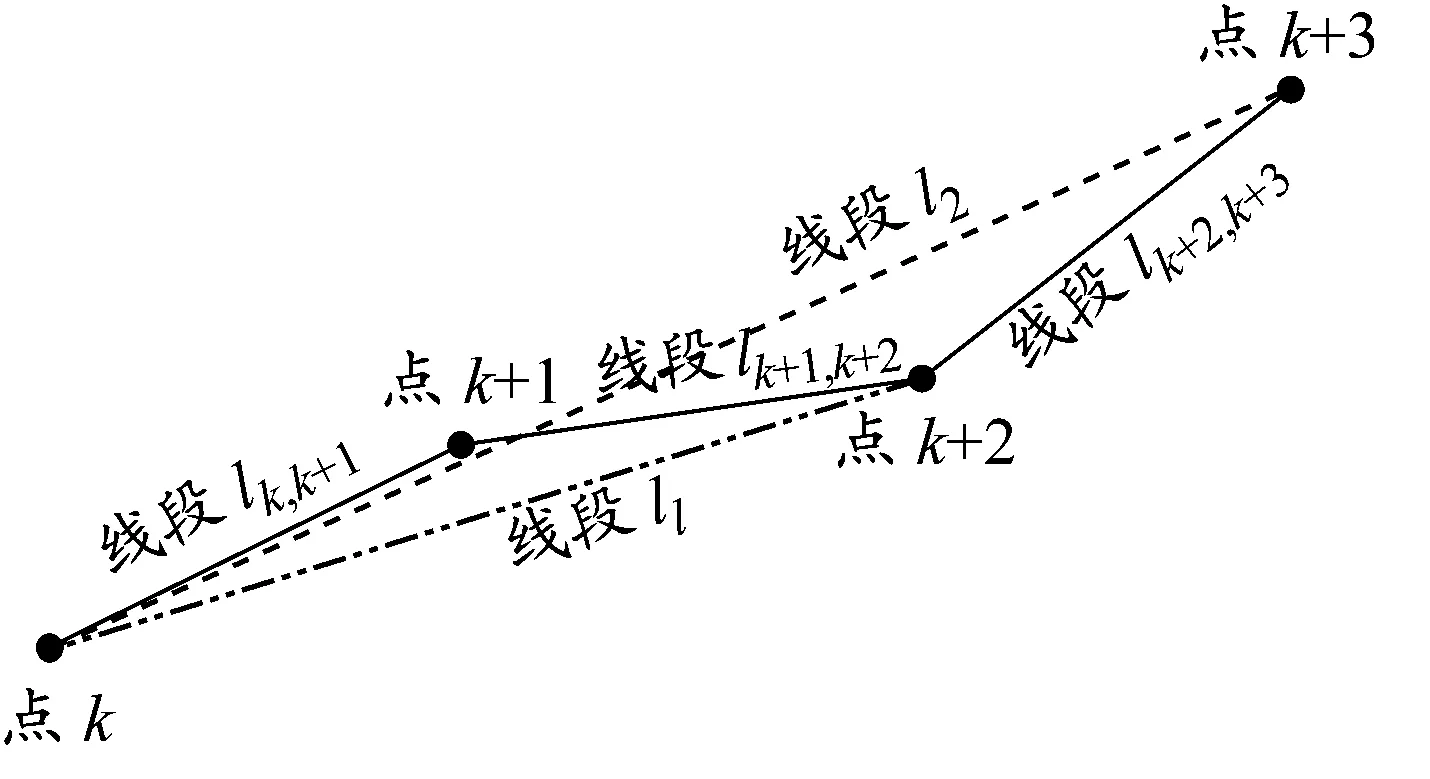
圖6 航路節點優化示意圖

經過試驗，傾斜角差閾值的取值對最終結果有較大的影響。取閾值分別為5°、10°和15°進行試驗，發現當閾值為10°時結果較為理想。取不同閾值時的優化結果見圖7。

由圖7b可以看出，最終的優化航路由起點、5個轉向點和終點組成，一共有6個航段。

5 結 論

針對復雜水域船舶航路規劃問題，建立了通航環境模型，基于遺傳算法和模擬退火算法設計了Memetic混合算法，對模型進行了求解，并從航海實踐角度對優化結果進行了實用化處理。實例驗證表明，本文設計的算法能夠快速規劃出給定環境下的最優航路，并可以對航路進行進一步實用化處理，使航路規劃結果更具有實際意義。本文所建立的航路規劃數學模型是將船舶視為質點，并未充分考慮船舶自身動態變化，后期航路規則研究將設置船舶安全領域、氣象條件等約束條件。

a)閾值為5°

b)閾值為10°

c)閾值為15°圖7 取不同閾值時的優化結果

參考文獻：

[1] 楊俊超, 史越, 馬海明. 一種人—自動化系統協作的無人機航跡規劃方法[J]. 計算機測量與控制, 2015, 23(9): 3216-3218, 3224. DOI: 10.16526/j.cnki.11-4762/tp.2015.09.084.

[2] 吳博, 熊勇, 文元橋. 基于速度障礙原理的無人艇自動避碰算法[J]. 大連海事大學學報, 2014, 40(2): 13-16. DOI: 10.16411/j.cnki.issn1006-7736.2014.02.013.

[3] 徐言民, 楊柯, 關宏旭, 等. 基于SAPSO算法的群橋水域航路規劃[J]. 中國航海, 2015, 38(3): 37-40.

[4] 徐言民, 楊柯, 關宏旭, 等. 基于混合SAPSO算法的簡化群橋水域航路規劃研究[J]. 武漢理工大學學報(交通科學與工程版), 2015, 39(3): 455-458. DOI: 10.3963/j.issn.2095-3844.2015.03.001.

[5] 吳劍, 張東豪. 基于卡爾曼濾波和D*算法的動態目標航路規劃[J]. 電光與控制, 2014, 21(8): 50-53. DOI: 10.3969/j.issn.1671-637X.2014.08.011.

[6] 鄒春明, 趙俊超, 楊柯, 等. 基于懲罰-PSO的群橋水域多約束航路規劃[J]. 中國航海, 2016, 39(2): 67-70.

[7] 馬文耀, 吳兆麟, 楊家軒, 等. 人工魚群算法的避碰路徑規劃決策支持[J]. 中國航海, 2014, 37(3): 63-67.

[8] 徐言民, 楊柯, 關宏旭, 等. 群橋水域特征分析及建模研究[J]. 武漢理工大學學報(交通科學與工程版), 2015, 39(2): 250-253. DOI: 10.3963/j.issn.2095-3844.2015.02.005.

[9] 韓超, 王贏. 一種基于改進PSO的無人機航路規劃方法[J]. 艦船電子工程, 2014, 34(4): 49-53. DOI: 10.3969/j.issn.1672-9730.2014.04.015.

[10] MOSCATO P. On evolution, search, optimization, genetic algorithms and martial arts: towards Memetic algorithms[R]. Pasadena, USA: California Institute of Technology, 1989.

[11] 劉漫丹. 文化基因算法(Memetic Algorithm)研究進展[J]. 自動化技術與應用, 2007, 26(11): 1-4, 18.

[12] 姚新, 陳國良. 模擬退火算法及其應用[J]. 計算機研究與發展, 1990(7): 1-6.

[13] 宋燕子. 基于模擬退火算法的啟發式算法在VRP中的應用[D]. 武漢: 華中師范大學, 2013.