基于PSO的BP神經網絡-Markov船舶交通流量預測模型

范慶波， 江福才， 馬全黨， 馬勇

(武漢理工大學 a. 航運學院； b. 內河航運技術湖北省重點實驗室 430063)

0 引 言

船舶交通流量的準確預測對于海事主管機關制定合理有效的水上交通組織方案，保障船舶的安全通航具有重要意義。同時，它可以指導港口部門準確把握船舶交通流的變化趨勢，合理規劃布局航道、碼頭、錨地等港口水域。

為對船舶交通流進行準確預測，國內外學者已經做了大量的研究并取得了相應的成果，如：馬曉波等[1]應用GM(1,1)灰色系統模型，通過引入殘差修正等方法對模型進行了優化，并用優化后的模型對長山水道的船舶交通流量進行了預測；李曉磊等[2]通過構建自回歸滑動平均模型消除了趨勢成分和季節等因素的影響，并對荊州港船舶月均流量進行了預測；鄭友銀等[3]構建了灰色自回歸模型，通過仿真對某港口船舶交通流量進行了預測；FENG等[4]構建了支持向量機模型對船舶交通流量進行了預測；CHEN等[5]運用優化小波最小二乘支持向量回歸模型對船舶交通流量進行了預測；楊雙雙等[6]運用非凸低秩約束模型對天津港水域船舶交通流量進行了預測。

因BP神經網絡和Markov模型具有自身的優點，有很多學者將其應用到船舶交通流量預測中。翟久剛等[7]將基于BP神經網絡和殘差分析的船舶交通流量預測方法用于對長江九江大橋月度船舶交通流量的預測；郝勇等[8]利用遺傳算法對RBF神經網絡進行了優化，提高了港口船舶交通流量預測的精度；呂鵬飛等[9]將BP神經網絡與Markov模型結合，發揮了Markov模型對波動性大的數據預測精度高的優點，使預測精度得到了提高。然而，BP神經網絡和Markov模型各自也存在缺點：前者易陷入局部極小值、收斂速率慢；后者在求取狀態區間可能值和選擇白化系數的過程中存在誤差。

本文在前人研究的基礎上，構建BP神經網絡-Markov預測模型，充分利用BP神經網絡和Markov模型的優勢，并用粒子群優化(particle swarm optimization, PSO)算法對模型進行優化，以武漢長江大橋月度標準船舶交通流量為樣本進行預測，以期提高船舶交通流量預測精度。

1 模型構建

1.1 BP神經網絡模型

BP神經網絡算法是誤差反向傳播算法，其基本結構見圖1。

輸入層神經元的輸入為X(k)={y(k-1),…,

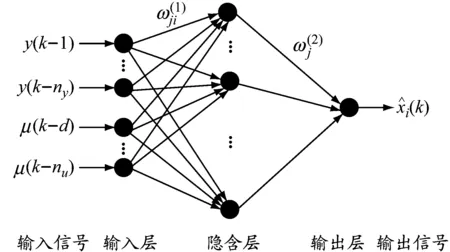
圖1 BP神經網絡結構

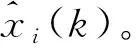
(1)

隱含層的激勵函數為log-sigmoid函數，即f(x)=1/(1+e-x)，估算隱含層神經元數量的公式為

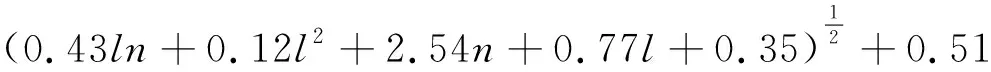
(2)

式中：n和l分別為輸入層和輸出層神經元數量。激勵函數的導數為

k時刻輸入層第i個神經元的輸出為

(3)

式中：i=1,2,…,n,n=ny+nu-d+1。

k時刻隱含層第j個神經元的輸入和輸出分別為

輸出層神經元的輸出為

(4)

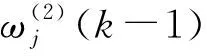
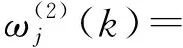
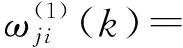
式中：α為動量項因子，α∈[0,1)。

1.2 BP神經網絡-Markov預測模型

Markov模型具有無后效性或Markov性。設一個具有Markov性的隨機序列為{Y(t)，t∈T}，T為離散的時間集合，E={E1,E2,…，Eλ}為狀態空間，則Markov模型的Markov性可以表示為

P{Yλ+1=Eλ+1|Y1=E1,Y2=E2，…，Yλ=Eλ}=

P{Yλ+1=Eλ+1|Yλ=Eλ}

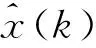
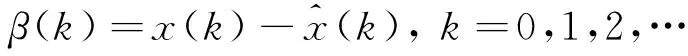
(5)

依據殘差序列將Markov模型劃分為λ個狀態，第i步的第j個狀態的上邊界和下邊界分別用Qij和Hij表示，計算方法[10]如下：

(6)

在每一個時間點，隨機過程中的每一個值只能處于一種狀態，每個狀態在接下來的狀態轉移中有λ個轉向(包括轉向自身)，即

{Ei→E1,Ei→E2,…,Ei→Eλ}

從狀態Ei經過1步轉移到狀態Ej的概率：

(7)

同理可得到l步狀態轉移概率：

(8)

系統的1步狀態轉移概率矩陣為

(9)

BP神經網絡-Markov預測模型的預測值為

(10)

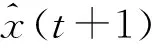
1.3 基于PSO算法的優化

在以上建模過程中，fi(i=1,2,…,λ)值的確定方法多種多樣，有的取狀態區間的中間值(白化系數取0.5)，有的運用黃金分割定律(白化系數取0.618)。這些方法都不具有普適性，誤差較大。本文引入PSO算法對上述模型進行優化，以根據數據序列的實際變化，求取最佳的白化系數。

PSO算法是由KENNEDY等[11]提出的，該方法簡單、高效、全局搜索能力強，因此被應用到很多領域進行模型優化。該算法模擬鳥群覓食行為進行社會性搜索，個體(也稱粒子)在超維度空間中飛行，而粒子位置的改變是受到群體中其他粒子的成功經驗及其自身的記憶影響的。

對于某個粒子i，其粒子群搜索公式為

vi(t+1)=wvi(t)+c1r1(xpbest-xi(t))+

c2r2(xgbest-xi(t))

(11)

xi(t+1)=xi(t)+vi(t+1)

(12)

式中：xi為粒子在t時刻的位置；vi為粒子在t時刻的速度；xpbest為群體微粒搜索到的自身最佳位置；xgbest為群體微粒經歷過的全局最好位置；r1和r2為服從U(0，1)的隨機數；w為慣性系數；c1和c2為學習因子。

本文用均方差EMS來衡量每個粒子的適應度函數：

應用粒子群算法進行全局搜索，求取最佳白化系數ai，狀態區間內可能的預測值fi求取方法為

fi=(1-ai)Qij+aiHij,ai∈[0,1]

(13)

基于PSO的BP神經網絡-Markov預測模型建立步驟見圖2。

圖2 基于PSO的BP神經網絡-Markov預測模型建立步驟

2 模型應用及分析

2.1 數據樣本的選取

標準船舶的選取是為了便于對不同水域相同時段或同一水域不同時段的船舶交通流量進行統計，更好地表征船舶交通流的概念。文獻[12]提到標準船舶作用有：實現不同航段船舶交通流量的比較，反映不同航段船舶交通流量的特點。日本運用“L系數”“L2系數”的方法進行標準船舶的確定，我國采用表1所示的換算系數將原始數據轉化為標準船舶數據。

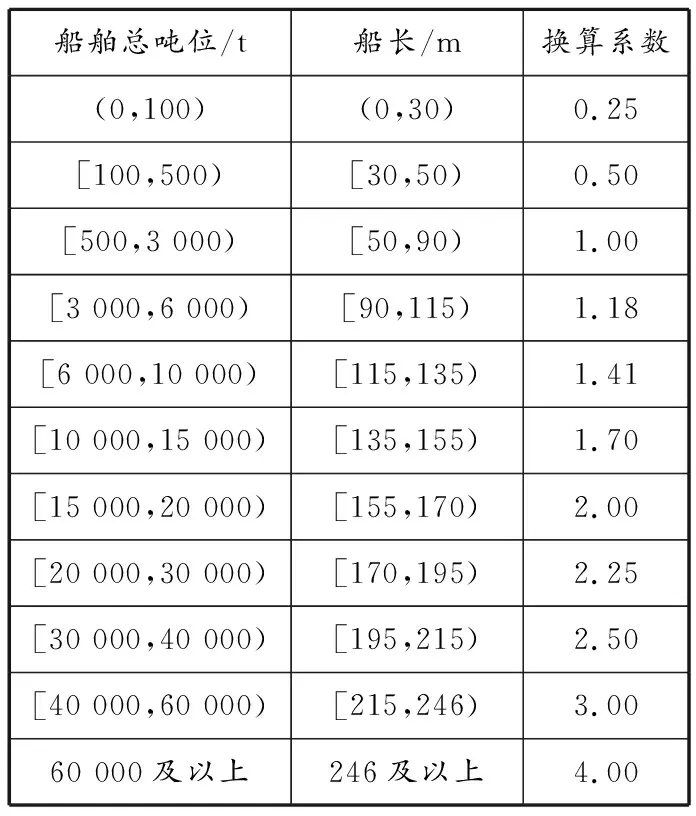
表1 標準船舶換算系數

根據表1中的換算系數，對從AIS軌跡流量分析軟件得到的武漢長江大橋2014年1月至2017年10月的船舶交通流量數據進行標準船舶轉換，得到的標準船舶交通流量見表2。

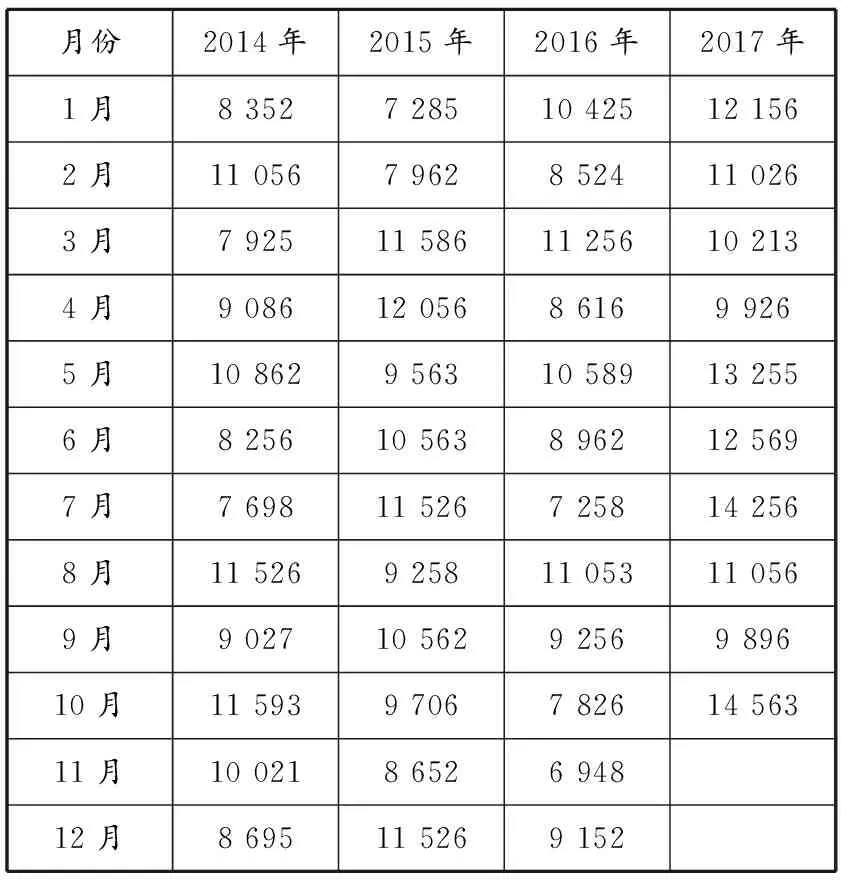
表2 武漢長江大橋標準船舶交通流量統計 艘次

2.2 BP神經網絡模型預測

2.2.1 數據預處理

為便于利用BP神經網絡模型進行預測，將表2中的數據劃分為如表3所示的43組樣本數據，以相鄰前3個月的船舶交通流量數據為樣本輸入值，第4個月的船舶交通流量為輸出值，如：2014年1—3月的標準船舶交通流量數據為輸入值，2014年4月的數據為輸出值。選擇前22組數據為訓練樣本，后21組數據為測試樣本。

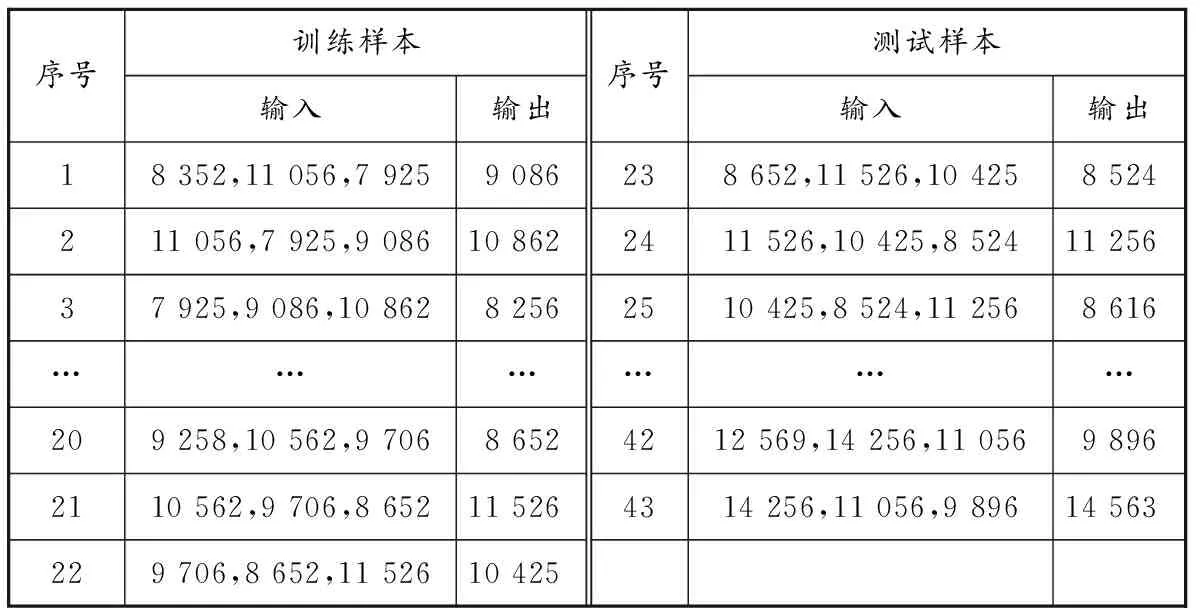
表3 43組樣本數據統計 艘次

2.2.2 模型結構及參數選取

選擇輸入層神經元數量為n=3，輸出層神經元數量為l=1。根據經驗公式(2)得到隱含層神經元數量m=4。本文選用的是mapminmax函數，訓練函數為trainlm，訓練次數為10 000次，訓練目標為0.000 01，學習函數為learngd，學習速率為0.01。

2.2.3 模型預測

運用MATLAB 2014a編制BP神經網絡輔助計算程序，訓練界面見圖3。

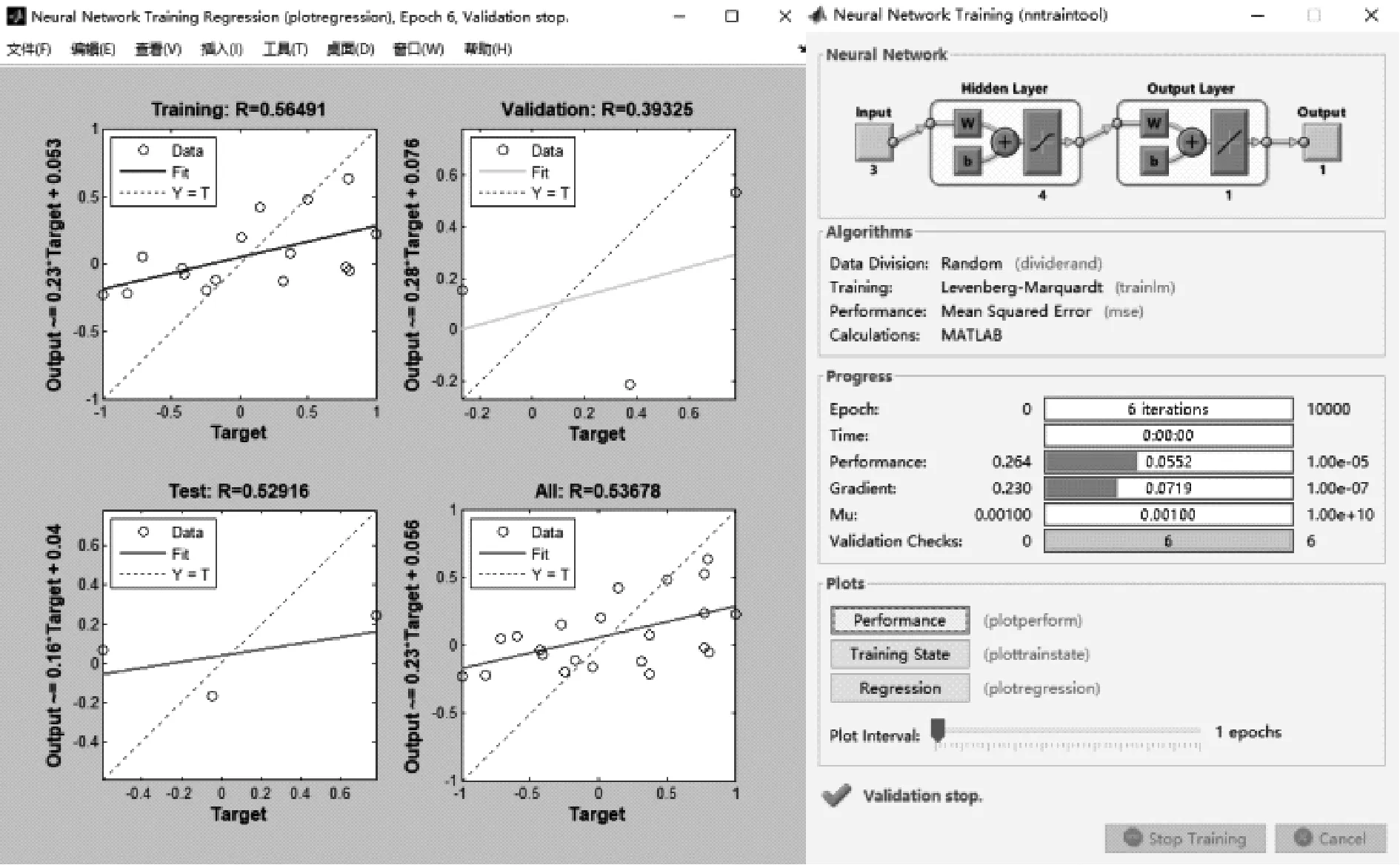
圖3 BP神經網絡訓練界面

選擇擬合相對較好、誤差較小的運行結果作為BP神經網絡預測值，結果見表4。

表4 BP神經網絡模型預測值和殘差 艘次

2.3 BP神經網絡-Markov預測模型

根據BP神經網絡的預測結果可以發現，單獨利用BP神經網絡進行預測，預測結果擬合效果較差。為提高預測精度，引入Markov模型對BP神經網絡模型進行優化。

2.3.1 狀態劃分

由表4可知，由BP神經網絡模型得到的標準船舶交通流量預測值殘差β(k)∈[-2 462,3 597]。按式(6)進行計算，將殘差序列劃分為4個狀態區間E1、E2、E3和E4，分別為[-2 462,-947.25)、[-947.25,567.5)、[567.5,2 082.25)、[2 082.25,3 597]。殘差狀態分布見表5。

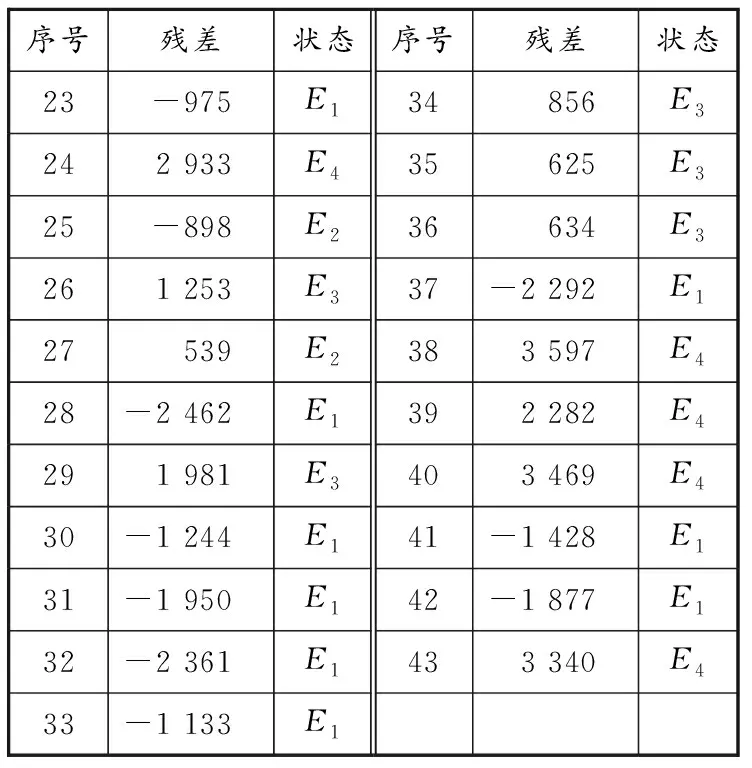
表5 殘差狀態分布

2.3.2 求取狀態轉移概率

根據表5中的殘差狀態劃分情況，對殘差的狀態從Ei經1步轉移到Ej的頻數進行統計，結果見表6。

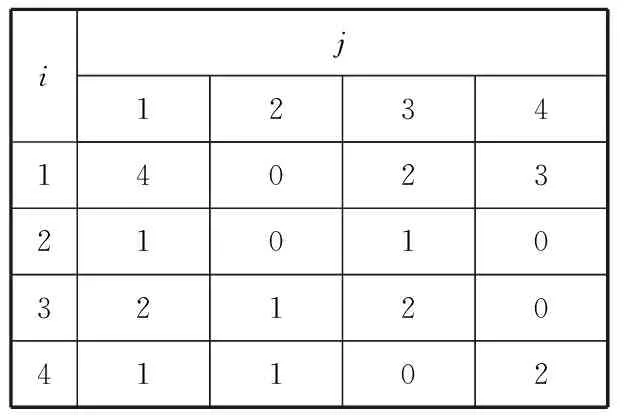
表6 1步狀態轉移頻數

經計算得到1步狀態轉移概率矩陣為

2.4 基于PSO算法的優化

灰區間(每個狀態區間)可能的值應該基于具體問題具體分析。本文引入PSO算法對BP神經網絡-Markov預測模型進行優化，根據樣本數據進行全局搜索，找到最佳的白化系數。

根據式(13)，對灰區間進行白化：

f1=-2 462a1-947.25(1-a1)

f2=-947.25a2+567.5(1-a2)

f3=567.5a3+2 082.25(1-a3)

f4=2 082.25a4+3 597(1-a4)

這里選取：粒子位置區間為[0，1]；粒子長度為4；慣性系數w=1；粒子數為1 000；粒子速度區間為[-0.01，0.01]；迭代次數k=1 000，學習因子c1=c2=2。運用MATLAB 2014a編制基于PSO算法的優化程序，輔助求解4個灰色系數(白化系數)，計算值如下：

a1=0.210 8，a2=1.000 0，

a3=0.968 6，a4=0.430 2

進而得到f1、f2、f3、f4的值如下：

f1=-1 266.56,f2=-947.25,

f3=615.06,f4=2 945.35

根據式(10)對預測值進行計算，計算結果見表7。

由表7可知，與單純利用BP神經網絡模型的預測結果相比，基于PSO BP神經網絡-Markov預測模型的預測值與船舶交通流量實際值更加接近。

2.5 誤差比較和預測

為便于進行誤差分析，運用平均絕對誤差和平均絕對百分誤差[10]對兩種模型的誤差進行分析。

從表8可知，本文模型預測精度為91.050 8%，高于單純利用BP神經網絡模型的預測精度，說明用該模型預測的船舶交通流量是可供參考的。下面運用該模型對武漢長江大橋2017年11月和12月的船舶交通流量進行預測。

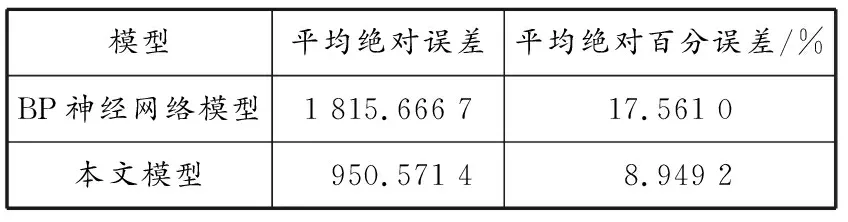
表8 兩種模型誤差比較結果統計

第43組數據轉移到第44、45組數據的1、2步狀態轉移概率矩陣分別為

根據式(7)和(8)計算兩組數據的1、2步狀態轉移概率：

(0 0.2 0.4 0.4)

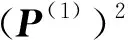
因為第43組數據的殘差處于E4狀態，所以第44組數據處于E3、E4狀態的概率最大，第45組數據處于E1狀態的概率最大。

得到2017年11月、12月的船舶交通流量分別為12 142/艘次、11 975/艘次。

3 結束語

本文提出了一種預測船舶交通流量的新方法，該模型在綜合考慮預測中非線性映射、殘差序列、狀態區間、狀態轉移概率的基礎上，自適應求解最佳白化系數，用以克服BP神經網絡和Markov模型在預測過程中存在的不足。基于粒子群優化(PSO)的BP神經網絡-Markov模型預測精度比傳統BP神經網絡模型預測精度高。計算結果可以為港口水域的合理規劃和相關主管機關制定合理有效的水上交通組織方案等提供參考。在后續的工作中還會在BP神經網絡存在的其他誤差、Markov模型最佳的狀態劃分方法、PSO算法的改進等方面進行研究，以期進一步提高預測精度。

參考文獻：

[1] 馬曉波, 劉雪菲, 戴冉. 優化的長山水道船舶交通流量灰色系統預測模型[J]. 上海海事大學學報, 2016, 37(2): 12-16. DOI: 10.13340/j.jsmu.2016.02.003.

[2] 李曉磊, 肖進麗, 劉明俊. 基于SARIMA模型的船舶交通流量預測研究[J]. 武漢理工大學學報(交通科學與工程版), 2017, 41(2): 329-332, 337. DOI: 10.3963/j.issn.2095-3844.2017.02.030.

[3] 鄭友銀, 徐志京. 基于灰色自回歸模型的船舶流量預測方法[J]. 船海工程, 2011, 40(1): 122-124. DOI: 10.3963/j.issn.1671-7953.2011.01.037.

[4] FENG Hongxiang, KONG Fancun, XIAO Yingjie. Vessel traffic flow forecasting model study based on support vector machine[J]. Communications in Computer and Information Science, 2011, 143: 446-451.

[5] CHEN Jinbiao, TIAN Yanhua, YING Shijun. Optimized LS-SVR method applied to vessel traffic flow prediction[C]//2010 2nd International Conference on Computational Intelligence and Natural Computing. Wuhan, China, 13-14 Sept, 2010: 315-320.

[6] 楊雙雙, 吳傳生, 劉釗, 等. 基于非凸低秩稀疏約束的船舶交通流量預測[J/OL]. 計算機應用研究, 2018, 35(1): 43-47[2017-01-19]. http://www.arocmag.com/article/02-2018-01-002.html.

[7] 翟久剛, 田延飛, 嚴新平. 基于BP神經網絡與殘差分析的船舶交通流量預測[J]. 上海海事大學學報, 2013, 34(1): 19-22. DOI: 10.3969/j.issn.1672-9498.2013.01.005.

[8] 郝勇, 王怡. 基于優化RBF網絡的港口船舶交通流量預測[J]. 中國航海, 2014, 37(2): 81-84, 117.

[9] 呂鵬飛, 莊元, 李洋, 等. 船舶交通量的BP神經網絡-馬爾科夫預測模型[J]. 上海海事大學學報, 2017, 38(2): 17-21, 28. DOI: 10.13340/j.jsmu.2017.02.004.

[10] 樊冬雪. 基于優化灰色馬爾科夫鏈模型的鐵路客流量預測方法研究[D]. 重慶: 重慶交通大學, 2015.

[11] KENNEDY J, EBERHART R. Particle swarm optimization[J]. IEEE, 2002, 4(8): 1942-1948.

[12] 馬勇. 基于排隊論的T型航路船舶交通通過能力研究[D]. 大連: 大連海事大學, 2008.