梁格法在城市橋梁設計中的應用分析

季 冬 良

(上海林同炎李國豪土建工程咨詢有限公司蘇通分公司，江蘇 南通 226000)

0 引言

隨著我國城市化迅速發展，城市的基礎設施建設越來越多，相應的高架橋梁和立交橋梁不斷涌現。為了滿足城市日益增長的交通運輸需求，橋梁的橋面寬度在不斷地增加相應的新型結構型式也在不斷發展，為了確保設計的橋梁結構型式能夠滿足運營壽命和使用安全要求，需要對橋梁結構計算分析進行準確把控。城市高架橋和立交橋中的寬梁橋、斜交橋和曲線橋等結構型式，采用傳統的平面桿系模型其實無法準確計算荷載橫向分布、橫向支座反力及其他內力集中效應，然而采用梁格理論可以很好地解決上述難題。

長期以來桿系模型廣泛用于橋梁的總體結構分析中，雖然具有計算簡單、分析明確的優勢，但不能滿足目前精細化結構設計需求，往往對內力(應力)集中等問題較難回答。實體計算理論又因為單元數量多所需要的計算代價較高，而梁格法則是介于其中的實用有效計算理論，具有概念清晰、易于理解和使用方便等特點。梁格法的基本理念是將橋跨結構分散為梁格體系，實際的構件通過區間劃分將其剛度等效到梁格上，通過對梁格分析計算其內力分布和變形，特別適用于城市高架和立交中的寬梁橋、斜交橋和曲線橋等結構型式[1，2]。

本文首先分析梁格法理論的基本原理，明確其理論基礎和適用性；其次闡述梁格法中梁格劃分方法和單元剛度計算方法，這是梁格法應用的兩個重要問題；再則闡述梁格法理論的分析優勢和不足；最后通過案例方式闡明梁格法在城市橋梁設計中的應用。

1 梁格法基本原理

梁格法的基本原理是用等效的兩個代替該區域的橋跨結構，并通過梁格之間的連接描述劃分區域之間梁體的相互關系，實際上梁格法是以梁為基本單元的有限元分析方法，但其相對于傳統的桿系模型而言可以較為準確的計算橫向受力特性。梁格法的概念明確、容易理解、方法易使用、計算速度快。

具體而言，梁格法將橋跨結構用等效的平面或者空間架構模擬，一般根據結構特點進行架構的劃分，每個劃分的區段內梁體的抗彎剛度和抗扭剛度直接等效到該梁格架構上，通過該平面/空間架構的分析就可以計算梁體的橫向受力、軸向受力和三維變形。對于箱梁截面而言，如果以腹板為單元進行梁格劃分，梁格的受力特點可以直接反演到腹板上，這樣可以直接進行腹板的配筋和設計，避免了采用空間有限元方法必須要對腹板進行內力橫向分布的環節，使得設計簡單計算準確。

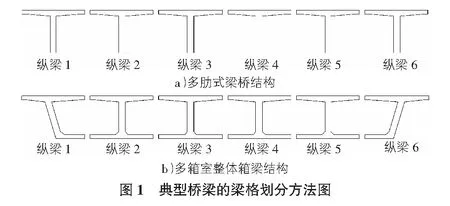
梁格法的關鍵是梁格劃分和單元剛度計算[3]：首先梁格劃分需要根據截面特點考慮，例如多肋式梁橋則將每個梁肋視為梁格，多室箱梁則將腹板視為梁格劃分標準，如圖1所示；其次是單元剛度的計算，應該使得計算的等效梁格體系在單位荷載作用下的變形和內力與原有結構相同，即等效性原則。

2 梁格劃分及單元剛度計算

2.1 梁格劃分方法

梁格劃分應該根據結構形狀及支座等進行確定，一般而言梁格劃分的一般性原則可以總結如下：

1)梁格劃分應盡量符合原型結構的內力分布特點及截面形狀，例如多肋式梁橋其受力是每個梁肋承擔，因此以梁肋為標準劃分；多箱室整體箱梁結構其受力是每個腹板承擔剪力流，因此應該以腹板為中心進行梁格劃分。

2)梁格劃分應盡量重合設計受力線，例如可以根據支座受力線進行梁格劃分，有效地模擬結構的受力狀態和變形狀況。

3)梁格的縱橫向間隔應該盡可能一致，使得梁格單元對于荷載作用下的響應特性足夠靈敏，如果某一個梁格劃分尺寸很小，則在受力分析過程中可能出現奇異矩陣導致計算結果出現誤差。

4)梁格模型的劃分應該盡量使得各個部分的形心位置和整體形心軸位置重合，使得梁格能夠最大程度反映原始結構的受力狀態。

2.2 單元剛度計算

根據梁格法基本理論，荷載作用下梁格的受力及變形狀態是以單元之間的剛度關系為依據進行分配的，因此梁格法計算的準確性取決于梁格單元是否能夠準確模擬原始結構的受力特性。不同的結構形狀其單元剛度計算方法也不相同，以下針對典型結構分析其單元剛度的等效計算方法。

對于板式結構，可以按照正交各向同性板計算梁格的等效剛度，如下式所示，計算的依據就是劃分區域內梁板的等效抗彎剛度和抗扭剛度。

i=h3/12;c=h3/6。

其中，i為單位板寬情況下構件的慣性矩；c為單位板寬情況下構件的有效抗扭參數；h為板厚。

對于箱梁結構，根據梁格劃分原則往往分類為多個工字梁：縱向單元特性的計算就是以工字梁為基礎確定其抗彎慣性矩，抗剪則以腹板承擔計算其腹板面積作為抗剪面積；橫向單元特性的計算則是兩塊板組成的空腹式截面，因此抗彎慣性矩就是兩塊矩形板在距離中性軸一定距離下的等效抗彎慣性矩，根據單元荷載作用下變形和受力等效的原則計算其截面特性。箱梁扭轉變形時，剪力流往往圍繞著頂板、底板和腹板的周邊流動，因此抗扭剛度可以認為是頂板和底板提供。

3 梁格法理論的分析優勢及不足

梁格法理論只要做好梁格劃分及單元剛度計算，其余的計算操作都很簡單，操作方便；梁格法相對于單梁計算模型，因為考慮了橫梁的剛度貢獻和傳力效應，因此計算結果相對于單梁模型更加準確，能夠分析橫梁的受力和變形特點，對于整體結構變形問題估計更加合理；梁格法相對于實體有限元模型計算的單元數量大大減少，且能夠根據計算內力情況直接進行配筋設計，因此相對實體有限元方法更加簡單實用。總體而言，梁格法特別適用于多肋式和多箱室結構的計算，相對于單梁模型計算結果更加準確且能獲得橫向構件受力情況，相對于實體有限元模型計算過程更加簡單且能直接根據計算結果進行配筋設計。

然而，梁格法理論本身的特點使得其應用存在一定的不足，首先梁格法對于剪力滯問題描述不夠準確，雖然其計算結果能夠表現頂板不同位置應力水平的差異，但是往往差異不明顯，相對于實體有限元結果計算的明顯剪力滯問題描述不夠；梁格法計算的結構變形和應力狀態往往介于單梁模型和實體模型之間，對于局部精細化設計問題采用梁格理論不能代替實體有限元的分析結果。

4 梁格法理論的應用分析

4.1 工程算例

某雙跨連續鋼筋混凝土實心板橋，橋面寬度12.8 m長度40 m，主體橋面寬8 m高1 m，兩側翼緣分別寬2.4 m高0.4 m，所用混凝土材料的基本參數如下：密度2 600 kg/m3,彈性模量35 GPa,泊松比0.167，采用梁格法計算其結構受力特點，并與實體有限元計算結果進行對比。根據梁格法理論，首先進行梁格劃分和單元剛度等效計算，梁格的劃分為了保證計算精度按照橫向1 m寬度考慮，兩側2.4 m的翼緣則按照1.2 m梁格尺寸確定，縱向尺寸1 m，詳細的梁格劃分如圖2所示，根據劃分的梁格單元計算其等效剛度。注意到由于左右兩側翼緣的高度不同，導致其截面形心位置與主體截面存在差異，計算中應該考慮對梁格2～3及10～11設置橫向剛性連接，保證兩者的受力和變形的一致性。

4.2 計算結果分析

表1是采用梁格法和實體有限元方法計算的自重作用下順橋向梁體的彎矩結果，可以看到梁格法的計算結果與實體有限元計算結果存在很好的吻合性，誤差基本在6%以內，無論是對于整體的彎矩情況還是特殊構件3的彎矩分配，說明了梁格法計算的準確性，用于城市橋梁設計計算具有很好的適用性。

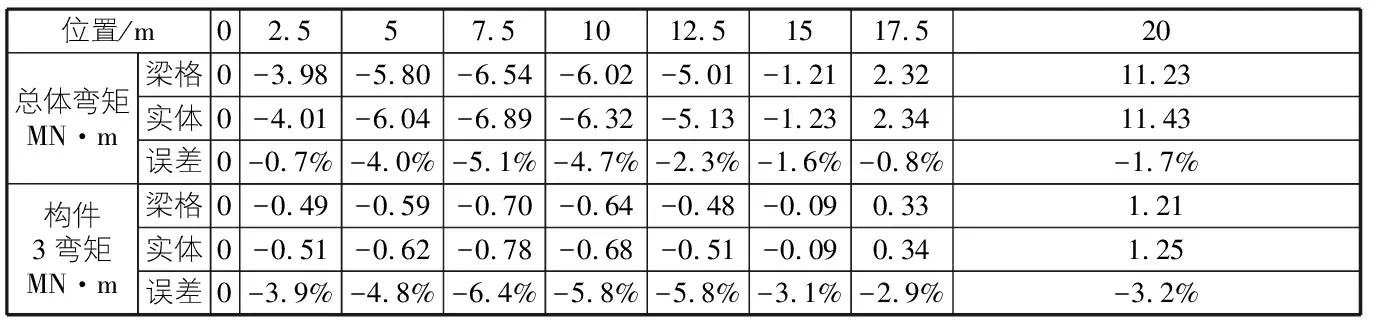
表1 梁格法計算結果與實體有限元結果的對比分析

5 結語

梁格法具有概念清晰、易于理解和使用方便等特點，非常適用于城市高架橋和立交橋中的寬梁橋、斜交橋和曲線橋等結構型式，本文分析了梁格法的基本理論及其關鍵技術，即梁格劃分和單元等效剛度計算兩個問題，并總結了梁格法的技術優勢和存在的不足，通過工程案例分析了梁格法在城市橋梁設計計算中的應用，并與實體有限元計算結果進行對比，誤差在6%以內，具有很好的精度，可以準確地用于城市橋梁的結構分析中。

參考文獻:

[1] 王富萬,楊文兵.梁格法在橋梁上部結構分析中的應用[J].華中科技大學學報(城市科學版),2006,23(S1):80-82.

[2] 王洪光.梁格法和單梁法在斜橋分析中的應用[J].交通標準化,2007(7):130-132.

[3] 王懷中,呂艷平.論梁格法在立交橋梁設計中的應用[J].廣東科技,2013,22(10):137.