淺海聲場相干特性研究
萬 駿
(三峽大學 湖北 宜昌 443003)
1 引言
當聲音在淺海中進行傳播時,淺海中的介質會引起聲音與聲音周圍邊界的非均勻聲散射,散射反向性的聲波會與聲源的接收器聲音產生疊加形成混響,散射的聲波會釋放能量引起接收信號聲波幅度發生較大波動,頻率產生非均勻變化。聲波受淺海影響會出現多段短聲波多途到達接收器,使得接受聲波在相位關系上存在著隨機性變化,因此會出現在同一淺海位置不同時間發出聲源,接受點回收信號會隨著時間發生不規則變化的現象。
接收點接受信號之所以會發生隨時間不規律變化很大程度上是受到了內波動等淺海海洋動力的影響。本文將進行公式推導與數值仿真兩種方式進行對于淺海聲場相干特性的研究,在仿真方面通過對于2014年南海海域中存在的數值標準進行仿真,在公式推導方面進行對于空氣聲源聲場相干特性分析與淺海聲源聲場相干分析共同進行,并尋找兩者的相干特性。
2 縱向水平相關簡正波計算
空氣與海水間存在比較大的聲阻,這就會導致聲源從水下發出聲波時,會發生某一點聲壓的數值正好是0的點,那就是軟邊界點。在現實中這一軟邊界的點存在在空氣與海水分割面上,根據簡正波的理論可以得出,位于水下的聲場可以利用下列方式來表達:

在這個公式中,H代表著海深程度,聲源深度用z來表示,其中的漢克爾第一類函數使用H0來代替的,在遠場中漢克爾函數還有一種近似表達式:
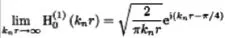
同時還有第二種可能就是聲源來源方式不同,當生源不是來自于淺海中而是存在空氣中時,就要進行對于聲音投射關系進行研究,第一種情況中的軟邊界就不存在了,取而代之的是從靜止空氣中將聲音傳遞到均勻介質的淺海內部,位于空氣中的聲源與空氣淺海分界點相距為h,淺海海深H,根據簡正波公式可以推導出:
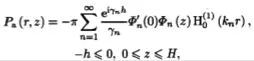
在公式中當z取值為0的時候,是公式一次微分z方向的值,根據一式與三式的對比可以得出,無論聲源的位置位于空氣中還是位于水中,對于相對同一位置的水下聲場來說,兩個公式中簡正波所對應的第N階簡正波時不變的,發生改變的只有每一號簡正波中存在的簡正波激發系數,即:

3 數值仿真
在計算中通過公式證明了空氣中進行的聲源發聲接受與淺海中進行的聲源發聲接受水平縱向相關特征是相對一致的,但是要進一步證明這一觀點,需要進行數值仿真實驗。仿真需要兩個聲源S與A,S是位于空氣中的,而A是位于淺海中的聲源,R作為接收器放置在海域深處,其中的參數設置與環境模型如圖1所示。

圖1 環境參數與環境模型
數據模擬的是在2014年5月份南海海域進行的一次真實實驗采集到的空氣聲實驗測量值。根據具體情況分析對于聲源的頻率采取125~131Hz,聲源深度采取四個方位,分別是-4.1m,-10.0m,4.1m與10.0m四個對應位置。模擬仿真使用軟件程序KrakenC進行對于聲源產生聲壓的計算,選取某一具體距離r當做統一標準,對于數據進行對于逆傅里葉變換并從中取得時域聲壓,對于淺海下聲場的相關系數水平縱向的仿真結果如圖2所示。

圖2 實驗淺海接受聲速
圖中以4.5km作為標準距離,圖中的曲線代表著相對不同的深度中,淺海下聲場相關系數水平縱向取值,進行對于數值對比會發現,當淺海中接受器與聲源的位置相對固定的時候,變化的聲源深度基本并不會影響到相關系數水平縱向,這也在另一個方面上證明了,空氣中的聲源與淺海中的聲源對應的相關系數水平縱向周期是并不會因為聲源位置發生改變的,這與之前得出的結論是相同的。
觀察數值變化幅度會發現,在-4.1m到-10.0m所對應數值的變化幅度相對比較小,但是當聲源深度在4.1m~10.0m之間,也就是當聲源存在在空氣中的時候,數值幅度會變得相對較大,前后兩段幅度變化差距較大。通過上面公式可以發現,當聲源位置在空氣中時,選取的淺海中對應有效聲源相關系數中的沒有發生變化的,所以當公式中其他參數發生變化時,對于結果產生的波動較大,所以才會出現圖中的數值較大波動。
4 結語
我國國防中一大重要研究主題就是水聲通信工程,這一項目也越來越多的應用在了海洋環境保護研究方面、海洋資源開發研究方面以及海洋數據收集研究方面,本文將海洋干擾通過數據公式形式展現出來,相對全面的展示了在淺海內力干擾下海洋聲波傳播損失與補充數值,相對具體的分析了海洋聲波波動頻率轉變方式與數據。通過公式的帶入與數值的仿真,本文得出了兩個結論:
(1)通過對于南海海域淺海空氣聲仿真數據得出,當以128Hz作為標準聲源頻率時,無論聲源存在的深度時空氣還是淺海,接收到的相關系數水平縱向結構都是相同的;
(2)通過對于公式分析與簡正波理論推導,延伸出了在空氣中聲源傳遞聲音與在淺海中聲源傳遞聲音的數字表達式。
[1]李風華,張仁和.淺海聲場相干特性研究[C]//全國水聲學學術交流會,2009.
[2]李秀林.淺海聲場水平縱向相干特性及其應用研究[J].聲學所博碩士學位論文,2004.
[3]彭漢書.淺海聲場矢量物理特性及應用研究[J].2007.
[4]朱良明.基于矢量水聽器的淺海矢量聲場特性及其應用研究[D].中國科學院大學,2015.
[5]孫梅,李風華,張仁和.淺海聲場垂直振速與水平振速相關特性及應用[J].聲學學報,2011(2):215-220.

