滿足最小裝機功率下的船舶波浪增阻數值計算研究
賈 騰, 董國祥, 高玉玲, 李傳慶
(上海船舶運輸科學研究所 航運技術與安全國家重點實驗室,200135)
0 引 言
在船舶能效權衡工作組(Working Group on Energy Efficiency Measures for Ships,EEWG)第1次會上,國際船級社協會(International Association of Classification Societies,IACS)提出了最小裝機功率概念,在海洋環境保護委員會(Maritime Environment Protection Committee,MEPC)61會議上,最小裝機功率被明確。在MEPC 61/5/32提案中IACS指出[1],當強制實施船舶能效設計指數(Energy Efficiercy Design Index,EEDI)時,船舶設計者若想船舶符合其標準,可選擇降低船舶設計航速,但是航速的降低勢必導致船舶推進功率的降低,這樣的船舶如果遇到極端海況,可能無法安全駛出危險區域。故此,IACS建議在EEDI規則中增加保證船舶安全性的條款[2],減少船舶在極端海況下的安全隱患。
要求得使船舶在極端海況下以最小前進速度行進所需的功率,就需要計算船舶在極端海況下受到的總阻力,包括空氣阻力、靜水阻力和波浪增阻。其中波浪增阻的計算是較為困難,且海況等級越高尤其是在極端海況下,波浪增阻在總阻力中占的比例較大,因此對計算波浪增阻的方法進行研究具有實際意義[3]。
船模試驗法和數值計算法是目前研究波浪增阻的主要方法。關于波浪增阻的數值計算,目前主要有基于二維切片理論、基于三維時域理論和基于黏流理論的3種數值方法[4]。基于黏流理論的數值方法主要是基于雷諾平均N-S方程的離散,與基于勢流理論的數值方法相比,能處理非線性流動現象,在處理甲板上浪及大幅運動等強非線性問題上具有極強的優勢,但是該類方法對計算性能要求很高,且計算速度較慢。相對于二維切片理論和黏流理論,基于三維時域理論的預報方法理論上計算效率更高。
利用基于泰勒展開邊界元方法對目標船在高速和低速下的波浪增阻進行計算,并與試驗結果進行對比,分析產生差異的原因。
1 計算方法
邊界元方法[5]可分為常值面元法和高階面元法,運用三維泰勒展開邊界元方法[6]會使非光滑邊界處切向誘導速度的計算精度得以改進。

圖1 坐標系及邊界示意
在有航速定解問題中,物面邊界條件及自由面邊界條件中均涉及速度勢的高階導數,利用泰勒展開邊界元方法,能精確求解非光滑流域邊界處流體運動質點切向誘導速度,為有航速定解問題求解提供了技術基礎。同時利用積分格式的自由面條件,解除了離散網格與時間步長需匹配的限制,在一定程度上提高計算效率。
建立平動坐標系O-xyz(見圖1)。xOy平面為靜水面,z軸垂直向上。無限水深中船舶以速度u沿著x正方向前進。匹配面SC將x流域D分成內域DIN和DOUT。DIN流域邊界包括船體濕表面SH,匹配面SC,內部自由面SF。Dout流域邊界包括匹配面SC,剩余自由面SF及無窮遠控制面。
對于有航速定解問題,總速度勢可分解為
φ=Φ+φd+φI
(1)
在內域中定解問題為
(2)
在外域中定解問題為
(3)
式(2)和式(3)中:vj為船體6個自由度的運動速度。
運用格林第三公式及邊界條件,可得到源-偶混合分布方法和分布源方法的邊界方程。三維分布源方法邊界積分方程為
(4)
式(4)中:σ為分布源源強;G為格林函數;s為浮體濕表面積。
2 模型試驗簡介
耐波性試驗設備采用四自由度適航儀及非接觸式超聲波浪高儀,伺服式傾角儀及加速度傳感器。造波機可造的最大波高0.3 m,頻率范圍為0.25~2.0 Hz。試驗在深水拖曳水池中進行,拖曳水池水深4.2 m,長和寬分別為192 m和10 m。
在試驗準備階段按照要求調整好船模慣量,使船模不僅滿足質量要求,還滿足重心和縱向轉動慣量要求。將模型與試航儀連接,應用四自由度適航儀拖曳模型,采用四自由度適航儀測量縱搖、垂蕩和阻力,浪高儀測量波高,加速度傳感器測量垂向加速度。
根據相應航速下測量的靜水中阻力,通過與規則波中阻力比較可得到波浪增阻。
試驗對象為57 000 DWT 散貨船,船模垂線間長為5.829 m,其主要參數見表1。
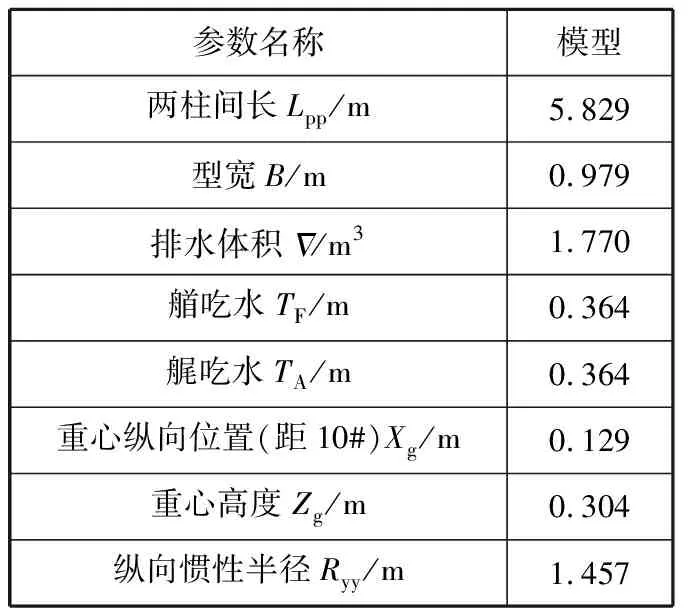
表1 散貨船基本參數
3 數值計算
船體計算模型見圖2,模型坐標系原點建立在船體中縱剖面與水線面的交線中部,模型為船體左舷半船模型。模型網格見圖3,除艏部區域和尾軸管區域采用三角形網格,其他區域均采用四邊形網格,自由面網格劃分選取45。根據經驗,縱搖慣性半徑和艏搖慣性半徑均選取0.25Lpp。選取了2個航速,分別為6 kn,11 kn,每個速度下從波浪頻率在0.366~1.035中取19個工況,各工況下的波高設定參照試驗波高。計算過程中每周期步長設置為30 s,模擬周期個數設置為9。

圖2 船體模型

圖3 船體面元網格
4 數值計算與試驗結果對比
采用基于三維泰勒展開邊界元方法計算得到低航速和高航速下的波浪增阻與模型試驗結果對比見圖4和圖5,兩圖均為波浪增阻頻率響應曲線,橫坐標和縱坐標分別為波長船長比和無因次波浪增阻。
通過對比發現,在低航速和高航速下計算結果與模型試驗結果的規律性一致,隨著波長與船長比的增加,波浪增阻均呈現先增大后減小的趨勢,均在波長與船長比為1.0附近達到峰值。航速為6 kn時,波浪增阻在波長船長比為1.0時達到峰值,數值計算結果比試驗值略大;航速為11 kn時,波浪增阻在波長船長比為1.2處達到峰值,數值計算結果與試驗值吻合性較好。

圖4 航速為6 kn時波浪增阻頻率響應曲線
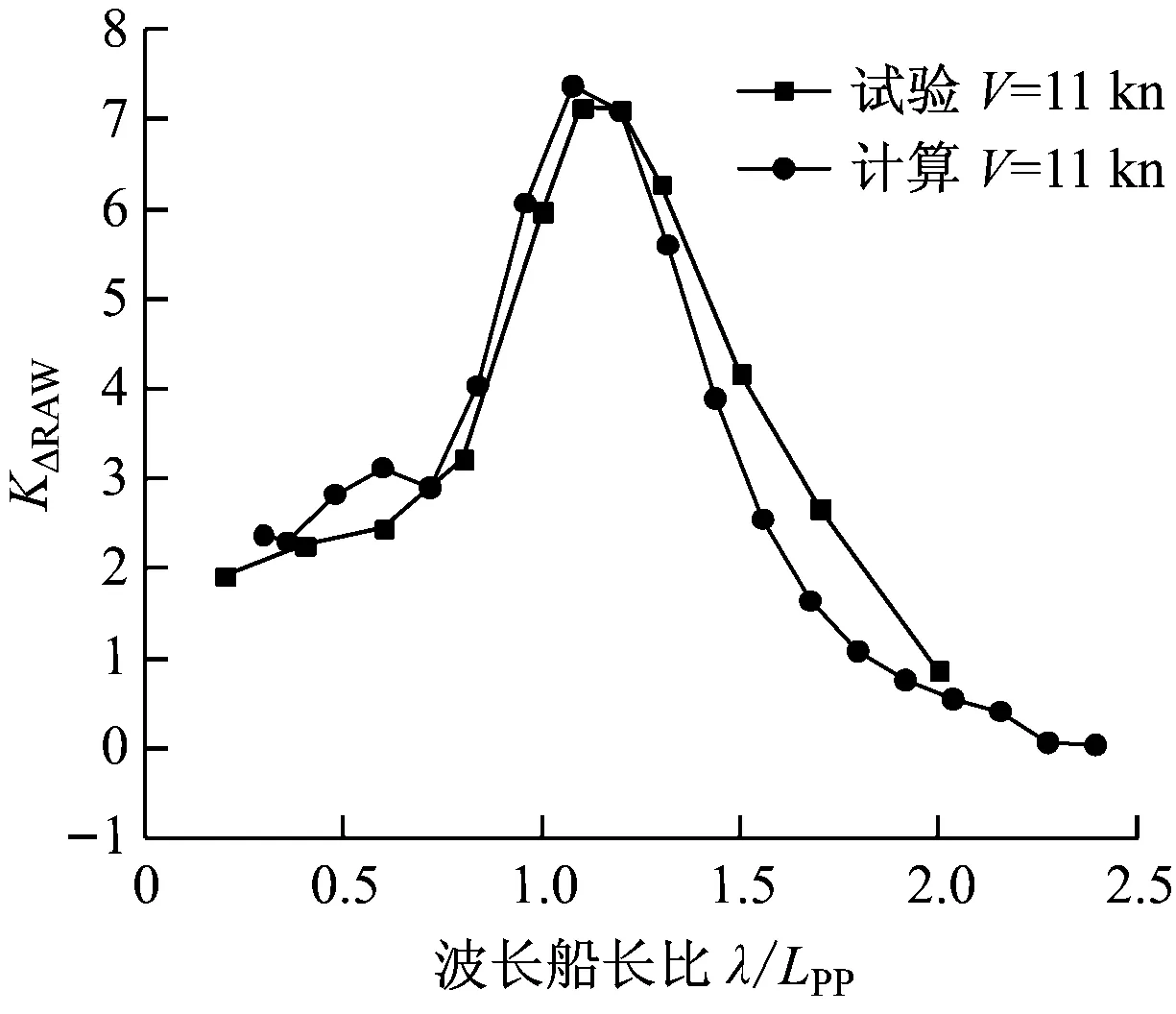
圖5 航速為11 kn時波浪增阻頻率響應曲線
5 結 語
利用基于泰勒展開邊界元方法的數值計算方法對一般散貨船在低航速和高航速下的波浪增阻進行數值計算,將數值計算的結果和模型試驗得到的波浪增阻進行對比分析。通過對比發現:數值計算結果與模型試驗得到的結果規律性一致,航速較高時計算結果與模型試驗的結果吻合性較好,但在低航速時計算精度略低,計算結果比試驗值略大,采用該方法對最小裝機功率下的波浪增阻進行評估較為保守。

