Zakharov-Rubenchik方程的有界行波解及其精確表達式

胡麗金，劉小華

（1.黔東南州民族職業技術學院 公共教學部，貴州 凱里 556000；2.貴州民族大學 數據科學與信息工程學院，貴州 貴陽550025）

Zakharov-Rubenchik 方程［1］是研究等離子體的重要方程，也是物理和數學研究領域的重要內容。 F.Oliverira［2］證明了空間上一維Zakharov-Rubenchik方程的整體適定性，還證明了該方程孤立波解的存在性和軌道穩 定 性 。 F.Oliverira［3］、J.Cordero［4］、李 志 斌［5］和H.Nishiyama 等［6］分別在(0 ≤ k ≤ l+1 2)空間上研究了Zakharov-Rubenchik方程的全局適定性。到目前為止，關于該方程精確解方面的研究還較少。在本文中，我們利用平面動力系統理論分析了Zakharov-Rubenchik方程的有界行波解的存在性，并利用待定系數法和指數函數展開法導出了該方程的鐘狀解和扭狀孤波解的精確表達式。

1　解的存在性

考慮以下Zakharov-Rubenchik方程：

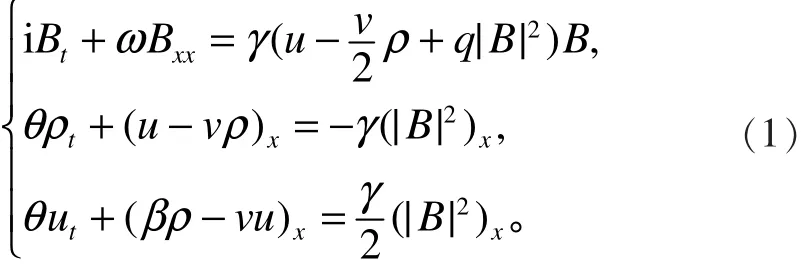
對方程（5）的第二式和第三式求不定積分，可以得到

將式（6）代入式（5）的第一式，令實部和虛部均為零,可得

下面借助平面動力系統理論分析系統（10）的相圖軌線。

情形 1：當m( c2+4 w λ) < 0時，系統（10）有一個平衡點時，P為鞍點；而當1時，P為中心點。1

情形 2：當 m ( c2+4 w λ) > 0時，系統（10）存在平衡點 P1、P2和 P3，且當時，P為鞍點，1P2和P3為中心點；而當時，P為中心點，1P2和P3為鞍點。

因為系統（10）是一個保守的平面動力系統，所以系統（10）的勢能函數為

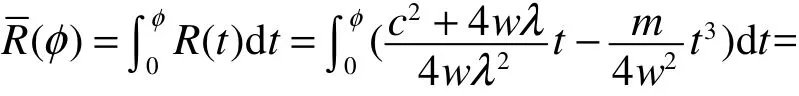
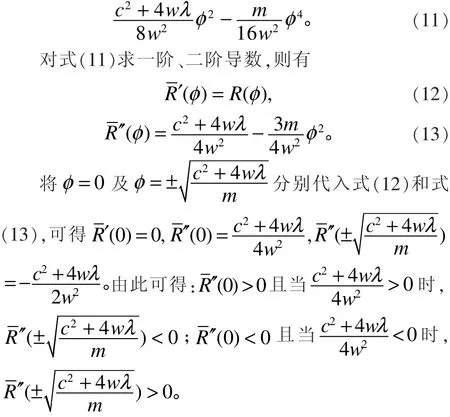
通過奇點分析可得系統（10）的相圖（圖1、圖2）。

圖1　時系統(10)的相圖

圖2　時系統（10）的相圖

從圖1和圖2可以看出，系統（10）同時存在兩條同宿軌線和異宿軌線，系統（10）的同宿軌線對應方程（8）的鐘狀孤波解，異宿軌線對應方程（8）的扭狀孤波解。

根據以上分析可得如下定理。

2　解的精確表達式

根據前面對方程（1）的定性分析，可假設方程（8）有如下形式

的解，其中A、B、D和r為待定系數。

對式（14）求一階和二階導數，可得