參數模型的預檢驗幾乎無偏兩參數估計

常新鋒，王和祥，左秀霞

（江蘇大學 財經學院，江蘇 鎮江 212013）

0 引言

考慮參數模型：

其中，y是n×1的觀測向量，X是n×p的觀測矩陣，β是p×1的未知參數向量，ε是n×1的隨機誤差向量，ε～N(0，σ2I)，σ2＞0。

模型(1)中β的附加信息為以下等式約束：

其中r為q×1的已知向量，R為q×p的矩陣，且q＜p。

對于模型（1），當不能確定等式約束條件式（2）是否成立時，考慮假設檢驗：H0:r=Rβ，H1:r≠Rβ。關于以上問題，其對應的似然比檢驗統計量為C=X′X，δ=Rβ-r。當H1成立時，統計量F為自由度為(q，n-p)的非中心F分布，非中心參數為(1 2)Δ，其中

對帶等式約束條件的參數模型（1），Judge和Bock[1]提出了基于F檢驗的預檢驗估計。考慮模型存在復共線性的情況，Saleh和Kibria[2]提出了基于F檢驗的預檢驗嶺估計。Yuksel和Akdeniz[3]得到了基于F檢驗的預檢驗Liu估計。Kibria和 Saleh[4]，Saleh[5]，Yang 和 Xu[6]等對各類預檢驗估計的統計性質進行了分析。Chang和Yang[7]提出了在t分布下基于W、LR和LM檢驗的預檢驗兩參數估計。本文在Wu和Yang[8]提出的幾乎無偏兩參數估計的基礎上，結合預檢驗估計的思想，提出了預檢驗幾乎無偏兩參數估計，并在均方誤差準則下對估計的統計性質做了研究。

1 估計的提出

為了解決參數模型（1）中的復共線性問題，Wu和Yang[8]提出了幾乎無偏兩參數估計，其表達式為：

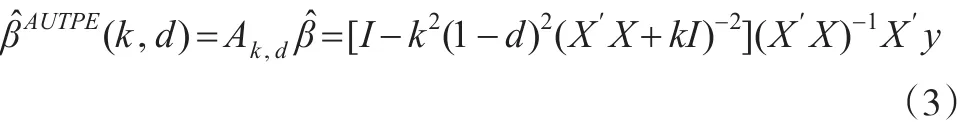
結合Kaciranlar等[9]得到約束最小二乘估計的方法，本文提出如下的約束幾乎無偏兩參數估計：

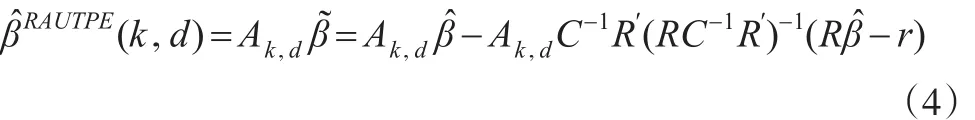
當不能確定等式約束條件式（2）是否成立時，本文得到基于F檢驗的預檢驗幾乎無偏兩參數估計

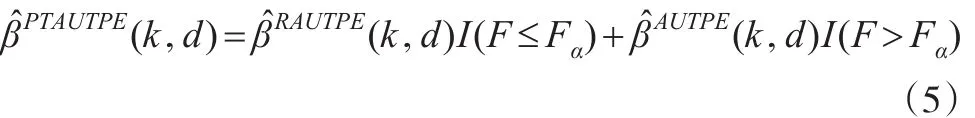
其中I(A)為事件A的示性函數，Fα表示自由度為(q，n-p)的中心F分布的上α分位數。

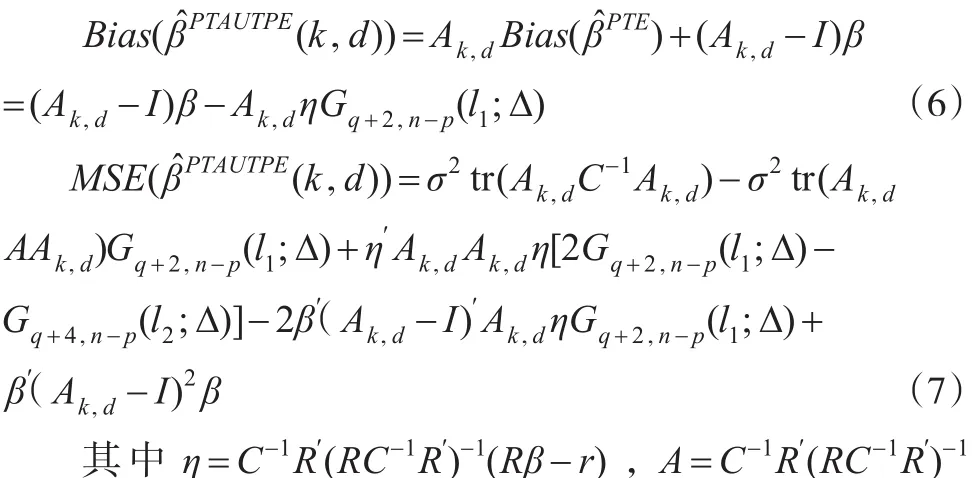
2 估計的性質

2.1 估計的均方誤差值為Δ的函數

引理1[10]：設矩陣A，B均為n×n的實對稱陣，且B為正定矩陣，對任意n×1的非零向量x，有≤λ1(AB-1)成立，其中λ1(AB-1)和λn(AB-1)分別表示矩陣AB-1的最大特征值和最小特征值。

定理1：在均方誤差準則下，令k＞0和0＜d＜1不變，

證明：β?AUTPE(k，d)的均方誤差為：

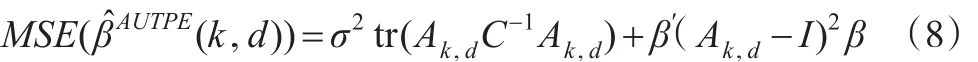
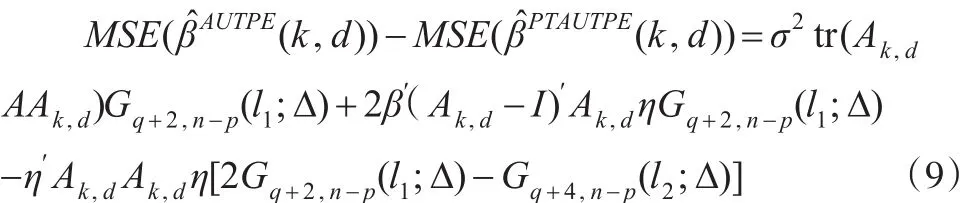
故MSE(β?AUTPE(k，d))-MSE(β?PTAUTPE(k，d))≥ 0 當且僅當：

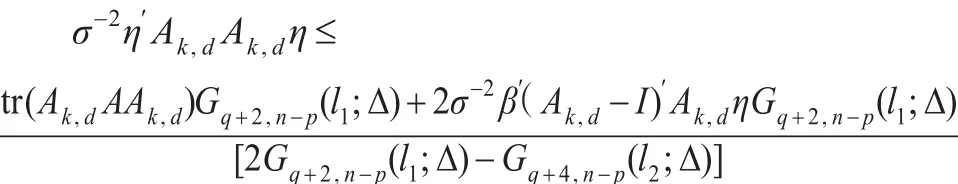
根據引理 1，得σ2Δλp(Ak，dAk，dC-1)≤η′Ak，dAk，dη≤σ2Δλ1(Ak，dAk，dC-1) 。 其 中 Δ=σ-2η′Cη，λ1(Ak，dAk，dC-1) ，λp(Ak，dAk，dC-1)分別表示矩陣Ak，dAk，dC-1的最大特征值和最小特征值。因此MSE(β?PTAUTPE(k，d))≤MSE(β?AUTPE(k，d))成立的一個充分條件為Δ≤Δ1，其中：

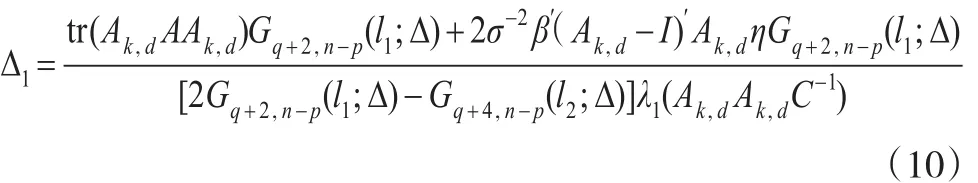
MS成立的一個充分條件為Δ≥Δ2，其中：

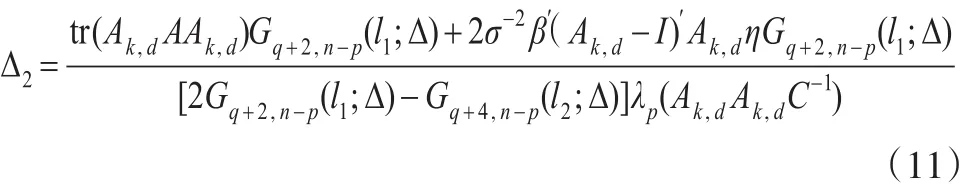
定理2：在均方誤差準則下，令k＞0和0＜d＜1不變，當當

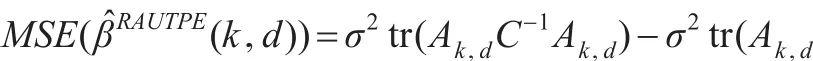
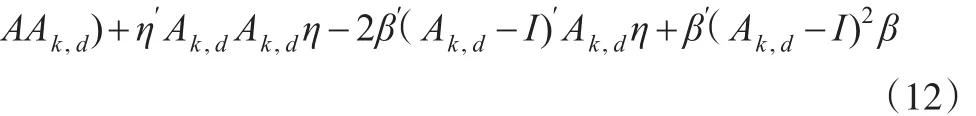
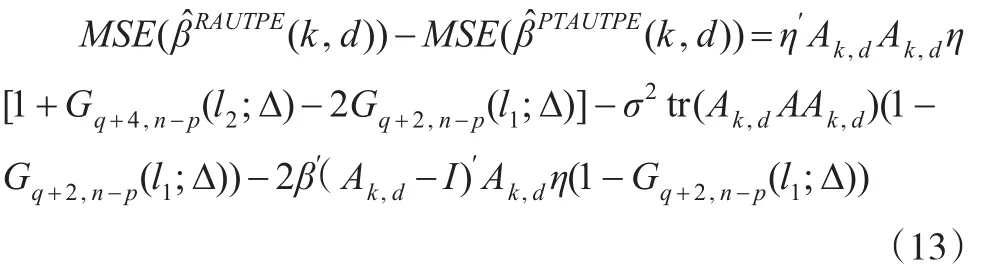
故MSE(β?RAUTPE(k，d))-MSE(β?PTAUTPE(k，d))≥ 0 當 且僅當：

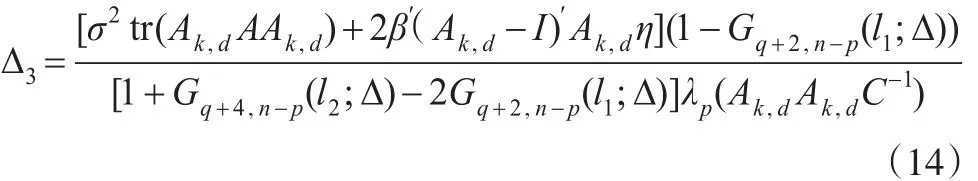
M成立的一個充分條件為Δ≤Δ4，其中：

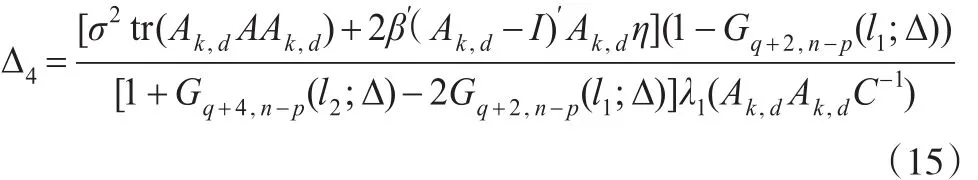
2.2 估計的均方誤差值為參數k和d的函數

另矩陣P為正交矩陣，且滿足其中λ1≥…≥λp＞0為矩陣C的順序特征根。則式（9）和式（12）分別記為：

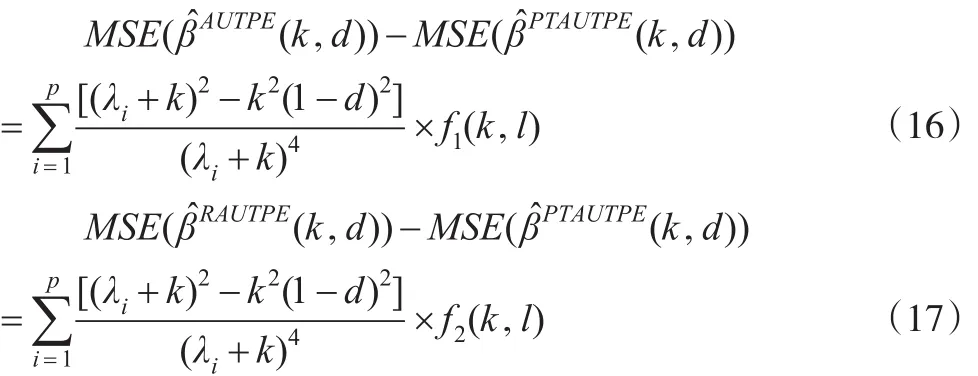
定理3：

（1）在均方誤差準則下，令 Δ＞0和 0＜d＜1固定，h1i＞0 ，當 0＜k＜k1時，MSE(k，d))≤(k，d)) ；當k＞k2時 ，(k，d))。

（2）在均方誤差準則下，對Δ＞0和k＞0固定，h2i＞0 ，當d1＜d＜1 時，d))；當 0＜d＜d2時，d))。

（1）令 0＜d＜1固定，f1(k，l)為參數k的函數，則若h1i＞0，此時關于參數k的一元二次函數f1(k，l)開口向下，其一正根為：

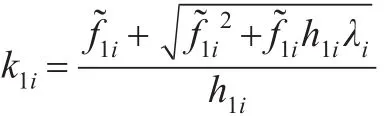
由于k=0 時，f1(0，l)=λi＞0 ，對任意的 0＜k＜k1，k1=min{k1i} ，有f1(k，l)≥0 ，故MSE(β?PTAUTPE(k，d))≤MSE對任意的≤0 ，故

（2）令k＞0固定，f1(k，l)為參數l的函數，則當h2i＞0時，關于參數l的一元二次函數f1(k，l)開口向下，其一正根為，對 任 意 的 0＜l＜l1i，有f1(k，l)＞0 。 而l=1-d，對任意的，有對 任 意 的有f1(k，d)≤ 0 ，故

定理4：

（1）在均方誤差準則下，令 Δ＞0和 0＜d＜1固定，h3i＞ 0 ，當k＞k3時，d))；當 0＜k＜k4時，d))。

（2）在均方誤差準則下，令 Δ＞0和k＞0固定，h4i＞0 ，當 0＜d＜d3時，(k，d))；當d4＜d＜1時，(k，d))。

（1）令0＜d＜1固定，f2(k，l)作為k的函數，則：

f2(k，l)=h3ik2+f?3i(2k+λi)

若h3i＞0，此時關于k的一元二次函數f2(k，l)開口向上，其一正根為：

其中

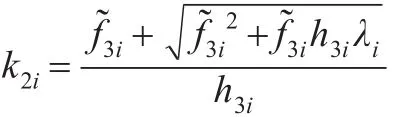
由于k=0 時，對任意的k＞k3，k3=max{k2i}，有f2(k，l)≥0 ，故對 任 意 的 0＜k＜k4，k4=min{k2i} ，有f2(k，l)≤ 0 ，故

（2）令k＞0固定，f2(k，l)為l的函數，則：

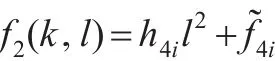
當h4i＞0時，關于l的一元二次函數f2(k，l)開口向上 ，其 一 正 根 為對 任 意 的l＞l2i，有f2(k，l)＞0。而l=1-d，對任意的對任意的0 ，故MSE

3 模擬分析

圖1 k=0.2和d=0.8時各估計在不同顯著水平下的均方誤差

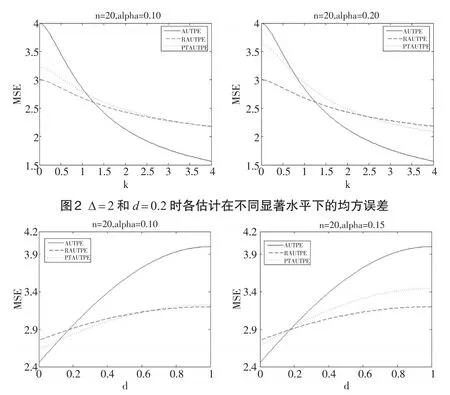
圖3 Δ=2和k=0.9時各估計在不同顯著水平下的均方誤差

從圖1發現，對于不同的α，β?PTAUTPE(k，d)，β?RAUTPE(k，d)和β?AUTPE(k，d)的均方誤差都隨著參數 Δ 的變大而增大。當Δ取值接近于0時，估計β?RAUTPE(k，d)的均方誤差值小于估計β?PTAUTPE(k，d)的值，同時估計β?PTAUTPE(k，d)均方誤差值小于估計β?AUTPE(k，d)。隨Δ值變大，估計β?PTAUTPE(k，d)，β?RAUTPE(k，d)和β?AUTPE(k，d)的均方誤差值的大小關系與上述情況相反。圖1中的均方誤差值變化情況驗證了定理1和定理2。

從圖2看出，對于不同的α，β?PTAUTPE(k，d)，β?RAUTPE(k，d)和β?AUTPE(k，d)的均方誤差都隨著參數k的變大而減小。當k取較小值時，β?RAUTPE(k，d)的均方誤差值小于β?PTAUTPE(k，d)的值，同時β?PTAUTPE(k，d)均方誤差值小于β?AUTPE(k，d)。 隨著參數k值變大，估計β?PTAUTPE(k，d)，β?RAUTPE(k，d)和β?AUTPE(k，d)的均方誤差值與上述情況相反。從圖3看出，對于不同的α，β?PTAUTPE(k，d)，β?RAUTPE(k，d)和β?AUTPE(k，d)的均方誤差都隨著參數d的變大而變大。當d取值較小時，β?AUTPE(k，d)的均方誤差值小于β?PTAUTPE(k，d)的值，同時β?PTAUTPE(k，d)均方誤差值小于β?RAUTPE(k，d)。隨著參數d值變大，估計β?PTAUTPE(k，d)，β?RAUTPE(k，d)和β?AUTPE(k，d)的均方誤差值與上述情況相反。圖2和圖3中的均方誤差值變化情況驗證了定理3和定理4。

4 總結

本文結合幾乎無偏兩參數估計和預檢驗估計，提出了參數模型的預檢驗幾乎無偏兩參數估計。在均方誤差準則下，分別給出了預檢驗幾乎無偏兩參數估計優于幾乎無偏兩參數估計、約束幾乎無偏兩參數估計的充分條件。通過數據模擬分析，驗證了上述理論結果。