基于GIOWHA算子的匯率組合預測模型

丁小松，楊桂元

（安徽財經大學 統計與應用數學學院，安徽 蚌埠 233000）

0 引言

過去對目標序列的預測都是借助于單項預測方法進行，但單項預測方法只利用了研究對象局部的有效信息，未能實現對研究對象整體信息的綜合利用，不能確保預測在所有的時點都具有較高的精度。為改變傳統預測方法的片面性，提高預測的精度，Granger和Bates（1969）提出了組合預測方法：通過賦予多種單項預測方法不同的權重，基于一定的優化準則，求解最優權重，實現對不同單項預測方法預測信息的充分利用，解決了單項預測的片面性，達到優于單項預測的效果。

過去的文獻主要有兩個研究方向：組合預測（點預測）和區間組合預測（區間預測）。如文獻[1]利用IOWHA算子組合預測模型對房地產價格進行預測，文獻[2]利用IGOWLA算子對區間序列構建組合預測模型進行區間預測，其實質為兩次點預測，即對區間左右端點進行預測，構成區間預測。而對組合預測模型研究的思路主要有兩種：一是直接研究預測值和實際值的擬合程度，具體方法有相關系數法、向量夾角余弦法等。如文獻[3]以實際區間半徑和區間中點與預測區間半徑和區間中點之間的相關系數最大為準則，構建多目標組合預測模型。文獻[4]則以實際值和預測值間的向量夾角余弦最大為準則求解組合預測模型中的權重。二是研究實際值和預測值之差即誤差項，方法有誤差平方和最小、誤差絕對值之和最小、最大偏差最小、貼近度最大、灰關聯度最大及Theil不等系數法等。如文獻[5]以實際序列和預測序列直接的貼近度為優化目標求解組合預測模型的權重，而文獻[6]則以灰關聯度最大為準則求解組合預測模型的最優權系數。

本文利用廣義誘導有序加權調和平均算子構建組合預測模型，以實際序列和預測序列的p次冪倒數誤差的平方和最小為準則，求解組合預測模型的權重向量，并以預測人民幣匯率序列說明所構建模型的預測效果。

1 相關概念及符號說明

設某序列第t期的實際觀測值為xt，共有n種單項預測方法，第i種預測方法第t期的預測值為xit，第i種方法第t期的預測誤差為eit，x?t為第t期的組合預測值，et為第t期的組合預測的誤差。其中i=1，2，…,n，t=1，2，…，N。

定義1：設OWAW:Rn→R為n元函數，W=(w1，w2，…，是和OWAW相關的權重向量，且ii=1，2，…，n。則稱：

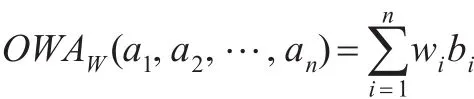
為n維有序加權算術平均算子，簡稱OWA算子，其中bi是 (a1，a2，…，an)由大到小排列的第i個數值。

定義 2：設 (＜v1，a1＞，＜v2，a2＞，…，＜vn，an＞)為 n 個二維數組，W=(w1，w2，…，wn)T為權重向量，且0≤wi≤1，i=1，2，…，n。則稱：

為n維誘導有序加權算術平均算子，簡稱IOWA算子。其中，v-index(i)是 (v1，v2，…，vn)（誘導變量）由大到小排列的第i大數的下標。

定義 3：設 (＜v1，a1＞，＜v2，a2＞，…，＜vn，an＞)為 n 個二維數組，W=(w1，w2，…，wn)T為權重向量，且≤wi≤1，i=1，2，…，n。則稱：

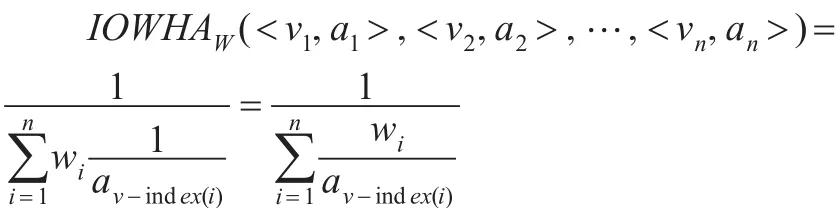
為n維誘導有序加權調和平均算子，簡稱IOWHA算子。其中，v-index(i)是 (v1，v2，…，vn)（誘導變量）由大到小排列的第i大數的下標。

定義 4：設 (＜v1，a1＞，＜v2，a2＞，…，＜vn，an＞)為 n 個二維數組，GIOWHAW:Rn→R為n元函數，W=(w1，w2，…，wn)T為權重向量，且則稱：

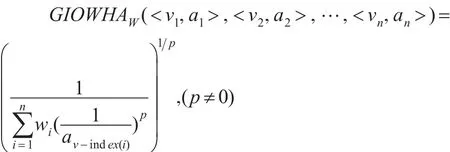
為n維廣義誘導有序加權調和平均算子，簡稱GIOWHA 算子。其中，v-index(i)是 (v1，v2，…，vn)（誘導變量）由大到小排列的第i大數的下標。

當p=1時，GIOWHA算子退化為誘導有序加權調和平均算子IOWHA；當p=-1時GIOWHA算子退化為誘導有序加權算術平均算子IOWA；當p→0時GIOWHA算子退化為誘導有序加權幾何平均算子IOWGA；當p→+∞時GIOWHA算子退化為min{ }a1，a2，…，an。（證明略）

2 基于GIOWHA算子的最優組合預測模型

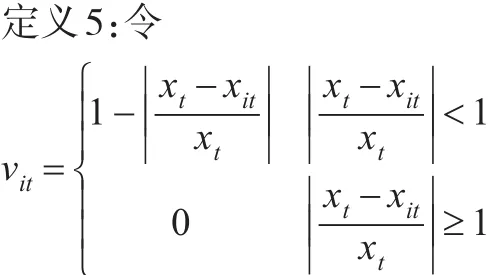
為第i種方法第t期的預測精度，其中vit∈[0，1]。以vit為誘導序列與各單項預測方法在t時刻的預測值相結合，可得 n 個二維數組 (＜v1t，x1t＞， ＜v1t，x2t＞，…， ＜vnt，xnt＞)，t=1，2，…，N。

定義6：令

的有序加權調和平均組合預測值，簡稱GIOWHA算子組合預測值。為誘導有序p次冪倒數誤差，i=1，2，…，n，t=1，2，…，N，則廣義誘導有序加權調和平均組合預測的p次冪倒數誤差為：

易知，GIOWHA算子根據不同時刻各單項預測方法的不同精度賦予不同的權重。以下使用p次冪倒數誤差度量組合預測方法的有效性。

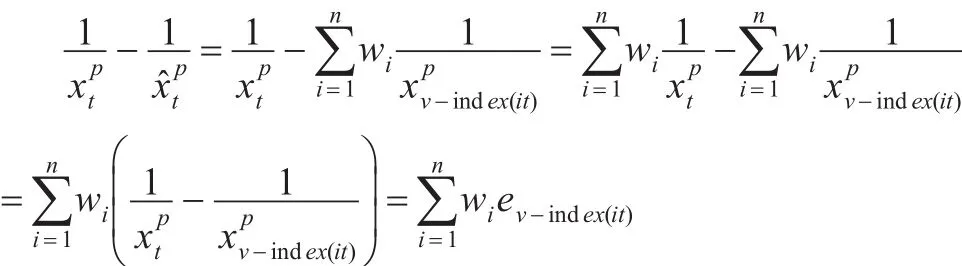
于是廣義誘導有序加權調和平均組合N期的組合預測p次冪倒數誤差平方和為：

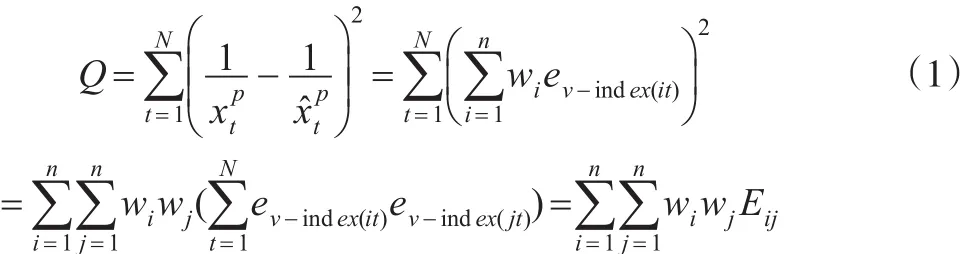
則基于誤差平方和最小的GIOWHA組合預測優化模型形式如下：

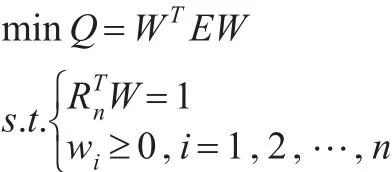
其中Rn=(1，1，…，1)T是分量均為1的n維列向量。

3 實例驗證

本文以2006年1月至2016年8月的人民幣匯率（直接標價法：一美元折合人民幣數）期末值為樣本，其中2006年1月至2016年2月的數據用于估計自回歸模型、多項式回歸模型以及局部多項式回歸模型，而2016年3月至8月的匯率數據用于驗證各單項預測模型與組合預測模型的預測效果，這樣做既考慮了內插預測誤差，又考慮了外推預測誤差，前者為模型內誤差，后者為模型外誤差。數據源于中國人民銀行官網。

圖1 2006.1—2016.8人民幣兌美元匯率時序圖

由圖1可知，人民幣匯率從2006年1月開始不斷升值，直至2015年7月開始貶值。

3.1 模型一（自回歸模型：AR（p））

自回歸模型的形式為：

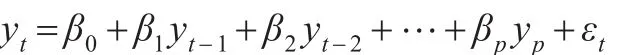
通過構建AR（1）、AR（2）和AR（3）可知AR（2）的估計結果最優，結果如式（2）：

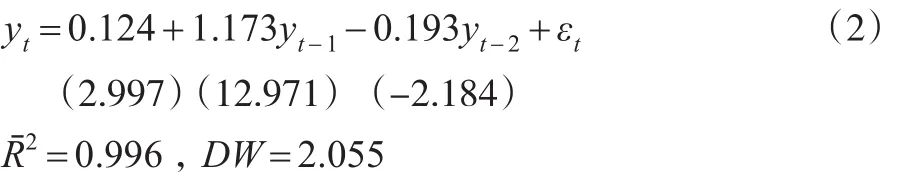
其中yt為即期匯率，yt-1，yt-2為匯率的滯后項，括號內的數值為估計參數的t值。

對殘差項序列相關性檢驗結果如表1所示，所估計的AR（2）模型的殘差項不存在序列相關性。

表1 LM檢驗

對殘差項進行ARCH效應檢驗即異方差檢驗結果如表2所示，所估計的AR（2）模型的殘差項無異方差性。

表2 ARCH效應檢驗

由表1和表2可知，AR（2）模型對匯率數據有很好的擬合效果，故使用AR（2）進行2016.3—2016.8的靜態預測，結果如表3所示：

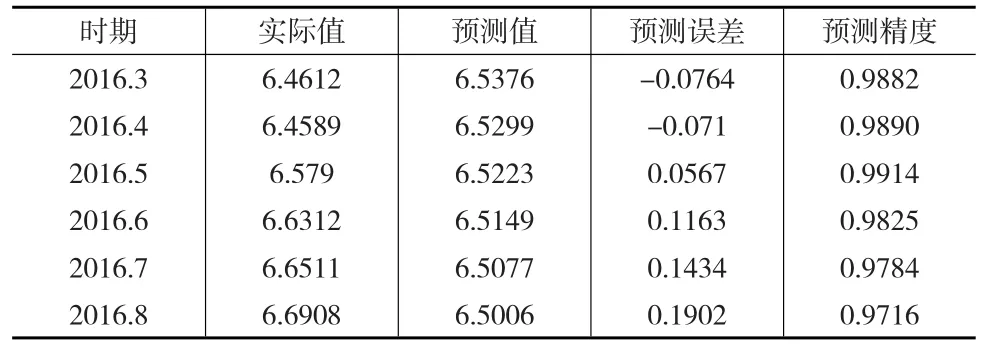
表3 AR（2）模型預測結果

3.2 模型二（ETS指數平滑狀態空間模型）

Pegel（1969）首先對指數平滑方法進行了分類，隨后Gardner（1985）對其進行了拓展，Hyndman等（2002）進行了修正，最后又被Taylor（2003）改進。

手術室護理始終是護理工作的研究熱點,因手術室護理質量直接關乎患者生命健康,尤其是手術實施過程中,任何手術失誤會影響手術效果、預后效果,不僅會增加患者的住院時間,增加患者經濟負擔,還會增加醫生、患者的精神壓力,引發醫患糾紛[3]。因此提升手術室護理,規避風險,提高手術室質量,具有重要意義。

本文使用加性模型，故可對時間序列做如下分解：

yt=Tt+St+Ct+εt

其中，T為長期趨勢，S為季節效應，C為循環變動，ε為不規則變動。ETS指數平滑狀態空間模型（以下簡稱ETS模型）中的E為誤差項、T為趨勢項、S為季節效應。E可以是加性的（A），也可以是乘性的（M），同時T和S可以是加性的（A）、乘性的（M）或者不存在（N），其中T可以細分為衰減加性（dampened additively簡稱Ad）或者衰減乘性（dampened multiplica-tively簡稱Md）。因此，指數平滑法一共有30種組合，包括線性的和非線性的，但只有15種具有乘性誤差項的可用于時間序列分析。

加性誤差模型：ETS（A，Ad，N）

令y?t=lt-1+bt-1表示yt的一步向前預測，εt=yt-y?t表示t時刻的預測誤差，假定所有參數已知。則空間狀態模型為：

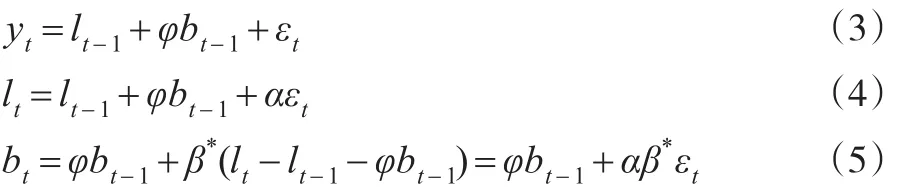
令αβ*=β，則式（5）可被簡化。由于式（3）至式（5）均包含誤差項εt，因此也被稱為新息狀態空間模型。

為得到空間狀態模型的標準形式，令xt=(lt，bt)T，將式（4）和式（5）帶入式（3）得：

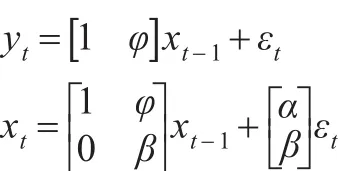
當εt的分布已知時，上述標準化的模型被完全識別，通常假定εt是獨立同分布的，即εt～N(0，σ2)。本文的ETS（A，Ad，N）模型中存在加性誤差項，衰減加性趨勢項，無季節效應。模型的估計結果如表4所示：

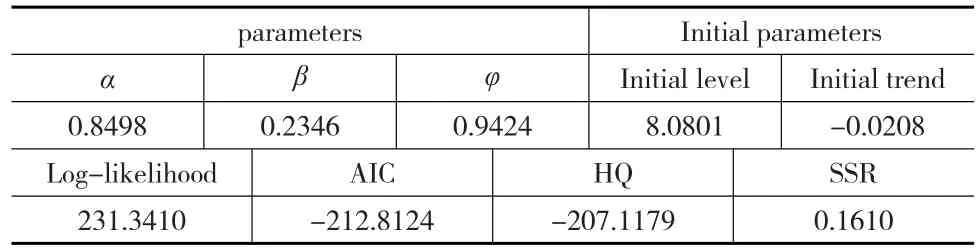
表4 ETS（A，Ad，N）模型估計結果

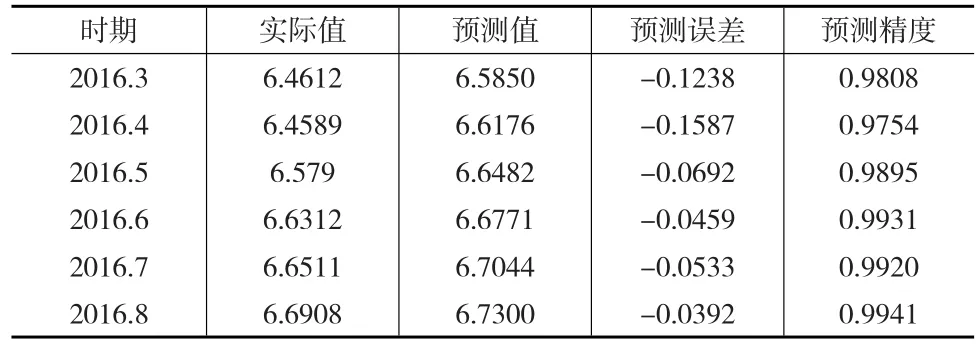
表5 ETS模型預測結果

3.3 模型三（局部多項式回歸）

非參數回歸中不需要對數據的生成過程做出具體的假定，其模型的形式通常為：

其中，m(x)為解釋變量的函數，e為模型的誤差項。

局部多項式估計的原理是使用多項式逼近m(x)。設m(x)在X=t處的p+1階導數存在，x為t鄰域內的任意一點，則m(x)的Taylor展開式為：

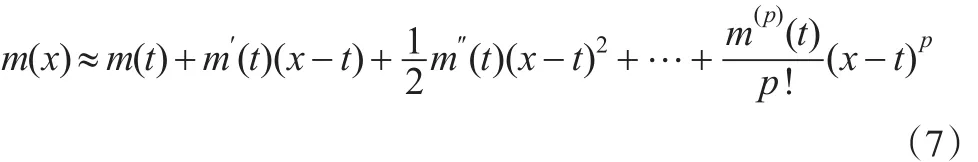
式（7）中m(p)(t)為m(x)在t處的p階導數，可視為待估參數，則式（7）可化為：

m(x)≈β0+β1(Xi-t)+β2(Xi-t)2+…+βp(Xi-t)p（8）

式（8）可由廣義最小二乘法進行估計，即最小化目標函數：

式（9）中 (X1，Y1)，(X2，Y2)，…，(Xn，Yn)為 (X，Y)的觀測樣本為權函數。本文選擇核函數epan2為權函數，擬合效果如圖2所示。

圖2 局部多項式擬合圖

當預測期數超過6期時，局部多項式回歸的擬合精度急劇下降，所以只進行6期預測，其預測結果如表6所示：

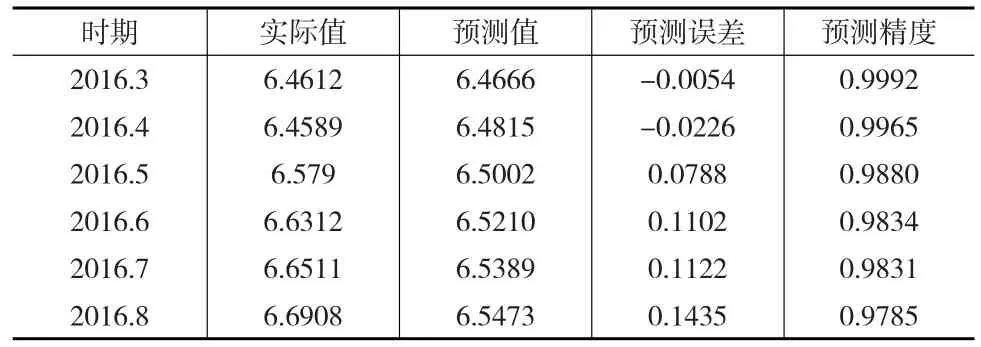
表6 局部多項式回歸模型結果

3.4 基于GIOWHA算子的組合預測模型

為對組合預測模型的有效性進行評，構建如下評價指標體系：

（3）均方百分比誤差

根據本文的三種單項預測方法在各時點的預測精度為誘導序列，對其在各時點的預測值進行誘導，則可以得到t時刻預測精度和預測值構成的二維數組：＜v1t，x1t＞，＜v2t，x2t＞，…，＜vnt，xnt＞ 。

當p=1時由定義（6）可計算GIOWHA組合預測值，其計算過程為：

（5）均方誤差

將上述結果帶入式（1），整理得如下模型：

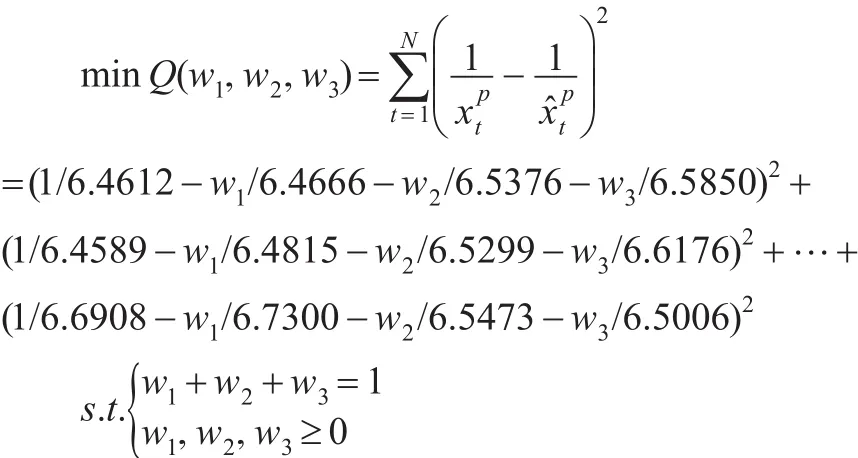
表7 基于GIOWHA算子的組合預測結果

為驗證GIOWHA組合預測模型的有效性，計算上述5項評價指標，結果如表8所示：

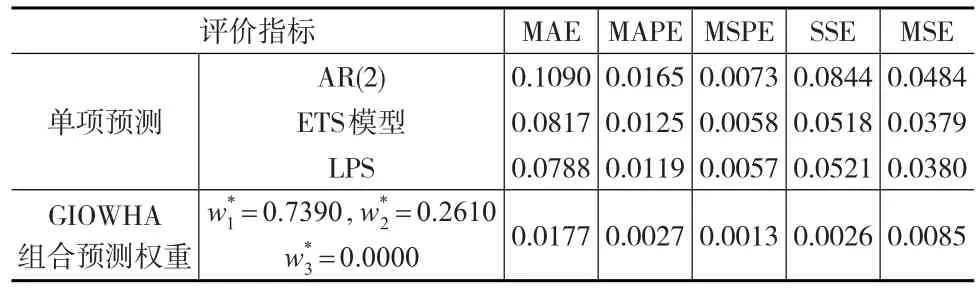
表8 單項模型和組合預測模型的外推誤差

由表8可知GIOWHA組合預測模型各項指標均優于單項預測方法，因此可初步得出其可改善預測精度的結論。

由表8計算的各種誤差指標為外推誤差，即模型外誤差，為充分評價組合預測模型的預測有效性，計算其模型內誤差，即內插誤差如表9所示：

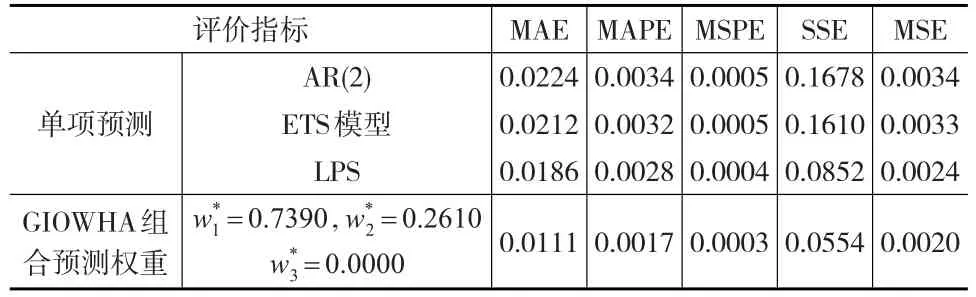
表9 單項預測模型與組合預測模型的內插誤差

由表9可知GIOWHA組合預測模型的內插誤差與各單項預測方法相比同樣是最小的，因此，與各單項預測方法相比，本文構建的基于GIOWHA的組合預測模型在內插誤差和外推誤差中均具有更優秀的表現。

4 結束語

本文以2006年1月至2016年8月人民幣匯率為研究對象，利用三種單項預測方法：自回歸模型、ETS指數平滑狀態空間模型和局部多項式回歸模型對匯率數據進行擬合預測。數據集被分為兩個部分，用2006年1月至2016年2月的數據估計模型，而2016年3月至2016年8月的數據則用于驗證模型的外推預測效果。然后建立基于誘導有序加權幾何平均算子（GIOWHA）的組合預測模型，以p次冪倒數誤差平方和最小為準則求得最優權重。最后利用多項評價指標對各模型的預測效果進行評價，發現基于GIOWHA的組合預測模型的模型內誤差和模型外誤差均優于三種單項預測模型，可以對匯率序列做出更精準的預測。