基于下側H-平均距離的風險度量

黃薏舟

（新疆財經大學 金融學院，烏魯木齊 830012）

0 引言

近幾十年來學者們對金融風險及其度量的研究逐步展開。Markowitz（1951）[1]提出了用方差作為風險度量的思想，但是該度量方法提出不久就受到許多質疑，為此他又提出了用半方差度量風險的思想。Konno和Yamazaki[2]則提出可以用投資收益的絕對離差度量風險的想法，并在此基礎上建立了他的投資組合模型。Yamazaki[3]則將Gini系數作為風險度量，并建立了均值-Gini模型。自Roy[4]提出用收益小于某個參照值的概率度量風險的想法后，對下側風險度量的討論漸漸多了起來。Bawa[5]提出了用下偏矩度量風險的想法，Fishburn[6]則提出了(α，t)作為風險度量的思想。以外，被提出的風險度量方法還有損失期望值、絕對半離差、β系數、在值風險、ES(Expected shortfall)、WCE等。

除了對風險度量方法的研究外，風險度量方法與隨機占優的一致性也是學者們的一個重要的研究內容。Porter[7]就證明了用關于某固定目標收益的半方差作為風險度量時，所導出的均值-風險模型與隨機占優是一致的。Yit?zhaki[3]證明了用Gini系數度量風險時均值-風險模型與二級隨機占優是一致的。Ogryczak和Ruszczynski[8]證明了半標準差作為風險度量時均值-風險模型與二階隨機占優是一致的，同樣的結論適用于絕對半偏差。Gotoh和Konno[9]將結果推廣到了三階隨機占優。Ogryczak和Ruszczynski[10]將上述結論進一步的推廣，證明了若以低于均值的k階中心半偏差作為風險度量，則均值-風險模型與二階隨機占優是一致的。

本文提出了一種新的風險度量方法并討論了該方法的性質。研究發現，該風險度量方法不僅涵蓋了一些常用的風險度量方法，而且與一級、二級隨機占優是一致的。因此，該風險度量方法具有一定的研究價值。

1 基于下側H-平均距離的風險度量

設X表示某種投資的隨機收益，Markowitz給出的風險度量為：

Yamazaki[3]提出了用Gini系數度量風險的思想，并討論了均值-Gini系數分析方法與二級隨機占優的一致性問題。設X表示投資的隨機收益，Gini系數被定義為：

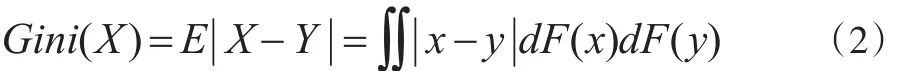
其中，Y是與X獨立同分布的隨機變量，F(x)為隨機變量X的分布函數。

從數學上看，方差度量的是隨機變量偏離其均值的程度，而Gini系數實際上就是隨機變量X到自身的距離。似乎方差和Gini系數沒有什么聯系，但給出方差的另一個定義，就會發現他們之間的聯系。方差還可以被定義為：

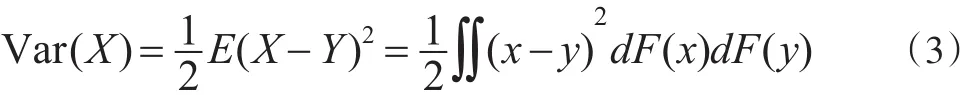
其中，Y是與X獨立同分布的隨機變量，F(x)為隨機變量X的分布函數。可以證明：方差和Gini系數都滿足非負性、對稱性和三角不等式，都可以用來描述隨機變量到自身的距離。

下面給出包含上述兩種距離的更為一般的H-平均距離的概念。

定義1：設X是與Y獨立同分布的隨機變量，H(x)為非負的凸函數，當x＞0時H(x)為單調遞增函數，當x＜0時H(x)為單調遞減函數，且滿足H(0)=0。稱E(H(X-Y))為隨機變量X到自身的H-平均距離。

可以證明：H-平均距離滿足非負性、對稱性和三角不等式三條公理。若F(x)為隨機變量X的分布函數，則隨機變量X到自身的H-平均距離為：

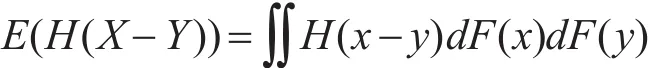
特別地，當H(x)=|x|時，H-平均距離即為Gini系數，當時，H-平均距離即為方差。可見，H-平均距離是上述兩種隨機變量到自身距離的推廣。

方差與Gini系數都可以用來度量風險，同樣，H-平均距離也可以用來度量風險。為此，構造如下形式的風險度量：

式（4）定義的風險度量雖然包括諸如方差、Gini系數等風險度量方法，但它也存在不足之處。一是方差就包含在該風險度量方法里，而均值-方差分析方法與二級隨機占優是不一致的，說明直接用于ρ1(X)=E(H(X-Y))度量風險與隨機占優之間存在不一致性。二是該風險度量不屬于下側風險范疇。根據Koszegi等[11]的思想構造X的風險度量：

其中H(x)為一定義在R+上的單調遞增的非負凸函數且滿足H(0)=0，Y是與X獨立同分布的隨機變量，(X-Y)+=max(X-Y，0)。

若F(x)為隨機變量X的分布函數，Y為與X獨立同分布的隨機變量，X的概率密度函數為f(x)，則X的風險度量為：

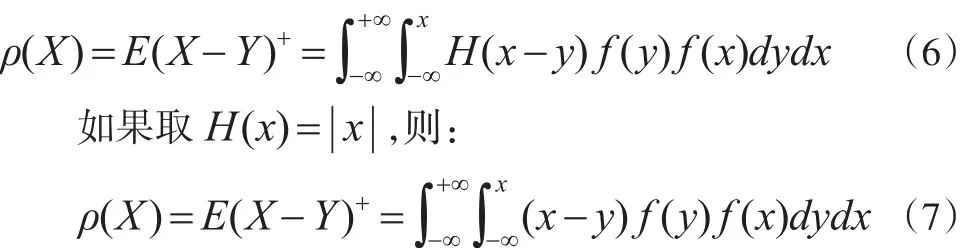
注意此風險度量與Gini系數不同。Gini系數是隨機變量X與自身的距離，而該值是隨機變量X與自身的下側距離，它明顯要比Gini系數小，稱之為下側Gini系數。

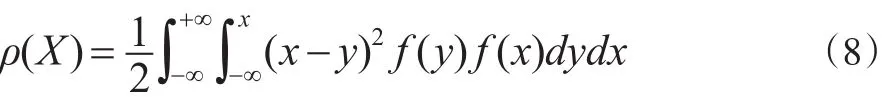
一般來講，此風險度量與方差也不同，它要比方差來的小。不妨稱之為下側方差。

2 風險度量的性質

要討論風險度量的性質，不得不說風險度量所滿足的公理。1999年，Artzner[12]等首次提出風險度量所滿足的四條公理，即平移不變性、正齊次性、次可加性、單調性公理。

公理1（平移不變性公理）：對于任意實數C，風險度量ρ(X)滿足ρ(X+C)=ρ(X)-C。

公理2（正齊次性公理）：對于任意正數λ，ρ(X)滿足ρ(λX)=λρ(X)。

公理3（次可加性公理）：對于任意隨機收益X，Y，ρ(X)滿足ρ(X+Y)≤ρ(X)+ρ(Y)。

公理4（單調性公理）：對于任意隨機收益X，Y，如果它們滿足X≤Y，則ρ(X)≥ρ(Y)。

Pflug[13]認為一致性風險度量公理的前三條具有一定的合理性，但單調性公理需要進行修改。他將單調性公理改為了協調性公理，定義如下：

定義2：假如風險X二級隨機占優于Y，即X?SSDY，則有ρ(X)≤ρ(Y)，則稱風險度量ρ(X)是協調的。

Giorgi[14]在對風險度量公理進行研究后，給出了凸風險度量的概念。

定義3：如果風險度量ρ(X)滿足：對于任意實數λ∈[0，1]，有ρ(λX+(1-λ)Y)≤λρ(X)+(1-λ)ρ(Y)，稱風險度量ρ(X)為凸風險度量。

那么，所構造的風險度量ρ(X)=E(H(X-Y)+)具有哪些性質呢？在討論之前，先介紹值函數的概念，將值函數定義為它的數學期望減去它的風險，即：

設F(x)為隨機變量X的分布函數，X的值函數可以表示為如下積分：

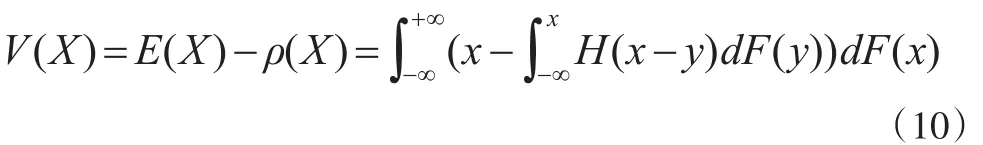
性質1：設H(x)可導且滿足0≤H′(x)≤1，若X?FSD Y，則V(X)≥V(Y)。

證明：設X與Y為兩個隨機變量，F(x)與G(x)分布為X與Y的分布函數。若X?FSDY，為證明V(X)≥V(Y)，構造函數，則u(x)的導數為：

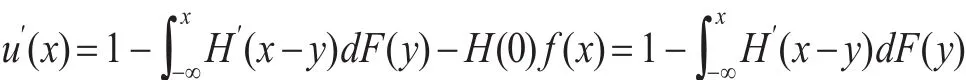
因 為H′(x)≤1,故 有dy≤1，所以u′(x)≥0 ，即u(x)是單調遞增的。根據Ha?dar-russel定理，若X?FSDY，則有Eu(X)≥Eu(Y)，即V(Y)。通過分部積分得到：

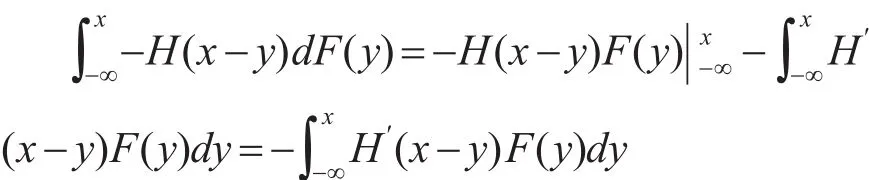
所以有：

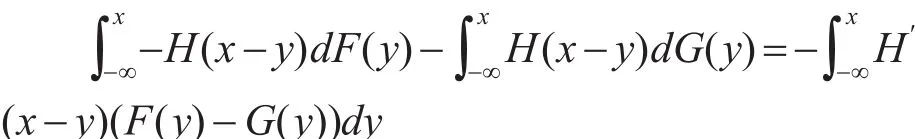
因為X?FSDY，所以F(x)-G(x)≤0 ，故有(x-y)(F(y)-G(y))dy≥0，假如存在x使得H′(x)＞0，則0 ，即：

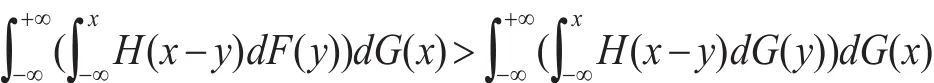
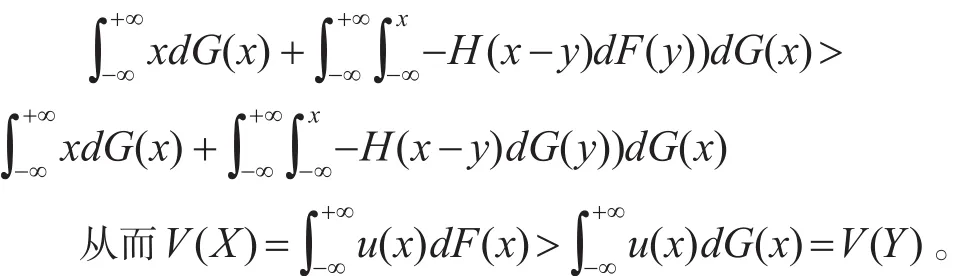
推論1：設H(x)可導且滿足0≤H′(x)≤1，若X?FSD Y，則對于任意實數λ(0≤λ≤1)，E(X)-λρ(X)≥E(Y)-λρ(Y)

證明：若X?FSDY，E(X)≥E(Y)。由性質1，E(X)-ρ(X)≥E(Y)-ρ(Y)。從而有：(1-λ)E(X)≥(1-λ)E(Y)且λE(X)-λρ(X)≥λE(Y)-λρ(Y)，相加得到：E(X)-λρ(X)≥E(Y)-λρ(Y)

稱λ為風險規避系數，稱E(X)-λρ(X)為決策函數。說明只要風險規避系數在0到1之間，決策函數與一級隨機占優是一致的。

性質2：設H(x)二階可導且滿足 0≤H″(x)≤1，若X?SSDY，則V(X)≥V(Y)。

證明：設X與Y為兩個隨機變量，F(x)與G(x)分布為X與Y的分布函數。若X?SSDY，為證明V(X)≥V(Y)，構造函數，則u(x)的二階導數為：

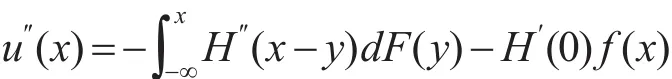
因為H″(x)≥0,H′(0)≥0 ，所以u″(x)≤0 。說明u(x)是單調遞增且凹的。若X?SSDY，根據Hadar-russel定 理 有，下 面 證 明，由于：

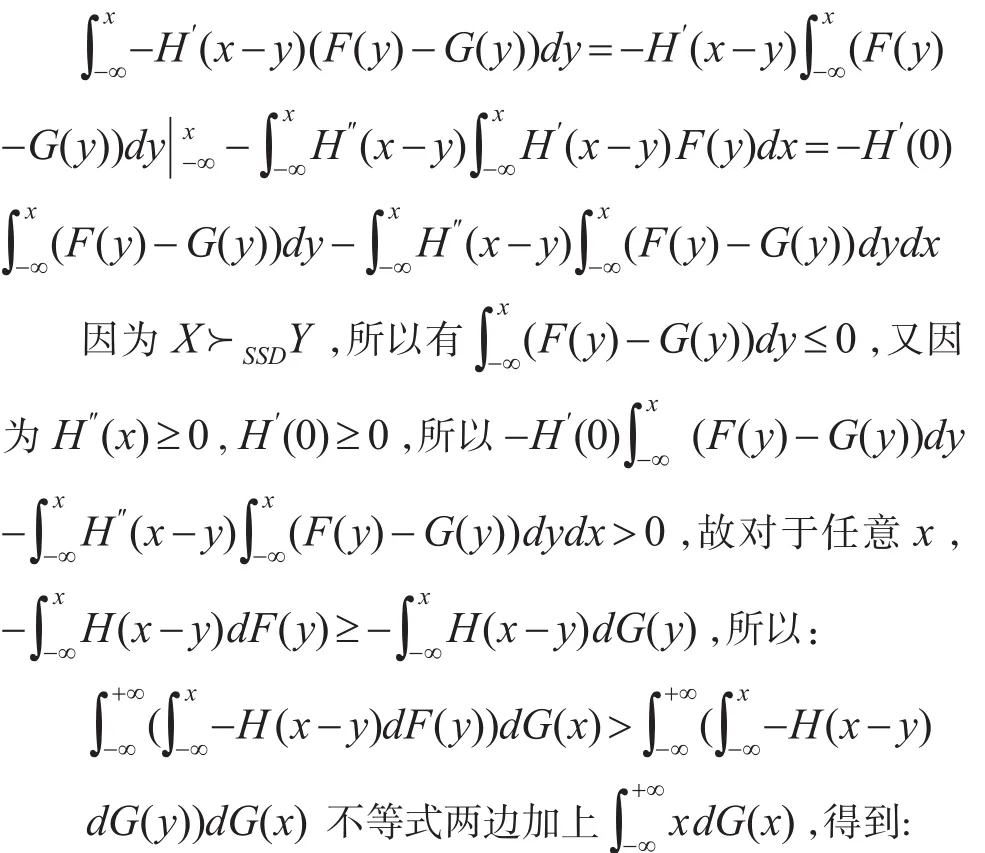
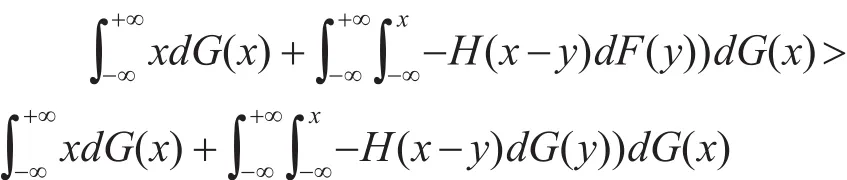
推論2：設H(x)二階可導且滿足 0≤H″(x)≤1，若X?SSDY，則對于任意實數λ(0≤λ≤1)，E(X)-λρ(X)≥E(Y)-λρ(Y)

證明：若X?SSDY，E(X)≥E(Y)。由性質2，E(X)-ρ(X)≥E(Y)-ρ(Y)。從而有：(1-λ)E(X)≥(1-λ)E(Y)且λE(X)-λρ(X)≥λE(Y)-λρ(Y)，相加得到：E(X)-λρ(X)≥E(Y)-λρ(Y)。

說明只要風險規避系數在0到1之間，根據決策函數所做的決策與二級隨機占優也是一致的。

性質3：風險度量ρ(X)=E(H(X-Y)+)為凸風險度量。

證明：因為ρ(λX+(1-λ)Y)=E(H(λX+(1-λ)Y-λX′-(1-λ)Y′)+)，其中，X′是與X獨立同分布的隨機變量，Y′是與Y獨立同分布的隨機變量。由于(λX+(1-λ)Y-λ X′-(1-λ)Y′)+≤λ(X-X′)++(1-λ)(Y-Y′)+，而H(x)為一定義在R+上的單調遞增的凸函數，故有：ρ(λX+(1-λ)Y)=E(H(λX+(1-λ)Y-λX′+(1-λ)Y′)+) ≤E[H(λ(X-X′)++(1-λ)(Y-Y′)+)]≤E[(λH(XX′)++(1-λ)H(Y-Y′)+]=λEH(X-X′)++(1-λ)EH(Y-Y′)+=λρ(X)+(1-λ)ρ(Y)

所以，ρ(X)=E(H(R-X)+)為凸風險度量。

綜上所述，建立在風險度量方法ρ(X)=E(H(X-Y)+)上的值函數V(X)，當凸函數滿足一定條件時不僅與一級隨機占優是一致的，還和二級隨機占優是一致的，這樣根據值函數V(X)所做的決策與期望效用理論也是一致的。

3 結論

本文通過對Markowitz提出的方差以及Yamazaki提出的Gini系數的研究發現，這兩種風險度量方法從本質上其實是隨機變量到自身的距離，只不過距離的定義有所不同罷了。既然隨機變量到自身的距離可以作為投資的風險度量，具有廣泛性的H-平均距離也可以作為投資的風險度量。所以本文首先定義隨機變量的風險度量為H-平均距離，但這樣給出的風險度量與隨機占優之間一般來講是不一致的，而且也不屬于下側風險范疇。基于上述兩點原因，本文將風險度量定義為隨機變量到自身的下側H-平均距離。下側H-平均距離作為風險度量較之H-平均距離作為風險度量有很多優良特性。首先，下側H-平均距離作為風險度量是凸風險度量，但H-平均距離作為風險度量則不是，因為方差就不是凸風險度量。基于凸風險度量在組合投資中的重要意義，所以，將風險度量修正為隨機變量到自身的下側H-平均距離是必須的。其次，H-平均距離作為風險度量一般與隨機占優是不一致的，這點從方差上就可以看出。而下側H-平均距離作為風險度量就不同了，研究發現建立在該風險度量方法上的值函數當滿足某些條件時，不僅與一級隨機占優是一致的，還和二級隨機占優是一致的，這樣根據值函數所做的決策與根據期望效用理論所做的決策也是一致的。鑒于以上兩點，基于下側H-平均距離的風險度量具有一定的研究價值和實際意義。